下载安装

用户可以点这里下载安装 MindOpt优化求解器

开通算法服务控制台 (免费的)

二次规划

在前文线性规划问题示例中，讲述到线性规划在我个人认为是在线性的目标和约束中，找出一个 最优解 。而本文的二次规划，是非线性规划中的一类。具体地说，是一个线性约束的、 二次规划 问题，就是优化（最小化或最大化）二次函数目标的问题。

关于优化的类别，有很多，比如MindOpt的案例广场的标签里面提到的问题标签，就列出了常见的数学规划的类型。其中关于 变量、约束、目标 这建模三要素，进行罗列：

关于变量：取值有连续的，有整数的，还有更特殊的二进制（0或1）的，
关于约束和目标：一般用变量的函数变换来表达，其中约束再增加它函数的取值范围。

- 当函数是变量的线性关系时，比如x的1次方相加，我们称呼为线性约束、线性的目标。（如果变量也是连续的，这个就是线性规划问题啦。）
- 当函数是变量的是二次关系的时候，比如函数中有 x的2次方项。我们称呼为二次约束，或二次目标。
- 函数还会有凸函数和非凸函数，数学里面都代表不同的特性，大家可以再多去查阅材料。

本文主要讲凸二次规划，Convex Quadratic Programming。

数学形式下的二次规划问题：

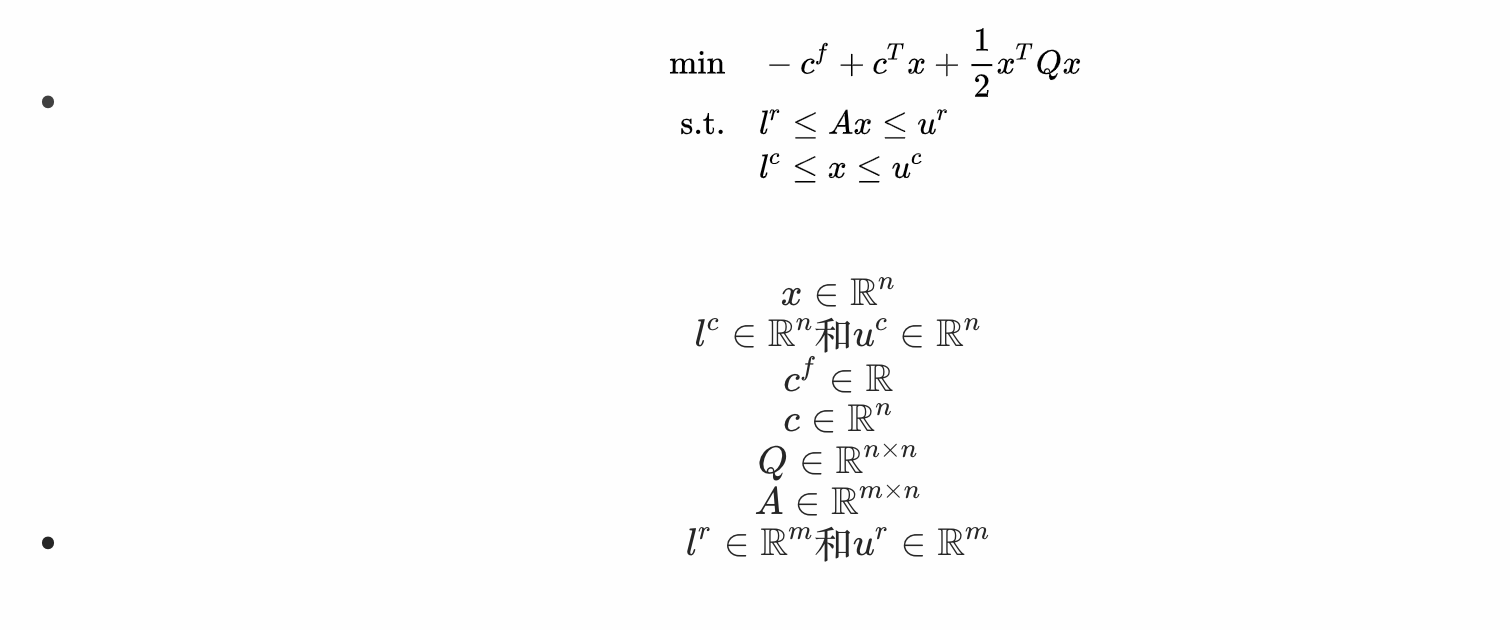
公式参考自MindOpt文档： https://solver.damo.alibaba.com/doc/html/model/qp/quadratic%20problem.html

案例

讲一个简单的例子，使用 二次规划 方法优化汽车轨迹，自动化驾驶车辆行驶在道路比较狭窄的路径上，还有其他障碍物阻碍的情况下，如果需要快速通过的话，我们需要暂时借用相邻车道通过，这个情况需要考虑自身车辆的情况、交通规则、保障远离障碍物距离的信息，然后找出一条通道。那么这个例子的解决办法是先考虑自身车辆的位置和周围障碍物，精确处理前一步可用车道，得到路径的边界，然后对路径边界进行优化 (比如把车辆和障碍物之间的距离 最大化 ，以允许车辆安全通过间隙)。

数学算例

接下来我们举一个简单的数学算例，和如何用MindOpt优化求解器进行求解。

二次规划问题示例：

C++和MindOpt代码实现

核心使用的几个APIs是：

 MdoModel model;
model.setIntAttr(MDO_INT_ATTR::MIN_SENSE, MDO_YES);
model.addCons(1.0, MDO_INFINITY, 1.0 * x[0] + 1.0 * x[1] + 2.0 * x[2] + 3.0 * x[3], "c0");
model.addCons(1.0, 1.0,          1.0 * x[0]              - 1.0 * x[2] + 6.0 * x[3], "c1");
model.solveProb();
model.displayResults();

下面是完整的例子，可复制存为 `MdoQoEx1.cpp` 文件。

#include <iostream>
#include <vector>
/*引入头文件*/
#include "MindoptCpp.h"
using namespace mindopt;
int main(void)
    /*------------------------------------------------------------------*/
    /* Step 1. 创建模型并更改参数。                */
    /*------------------------------------------------------------------*/
    /* 创建一个空模型。 */
    MdoModel model;
        /*------------------------------------------------------------------*/
        /* Step 2. 输入模型。                                             */
        /*------------------------------------------------------------------*/
        /* 通过 mindopt::MdoModel::setIntAttr() 将目标函数设置为 最小化 */
        model.setIntAttr(MDO_INT_ATTR::MIN_SENSE, MDO_YES);
        /* 调用 mindopt::MdoModel::addVar() 来添加四个优化变量，定义其下界、上界、名称和类型 */
        std::vector<MdoVar> x;
        x.push_back(model.addVar(0.0, 10.0,         1.0, "x0", MDO_NO));
        x.push_back(model.addVar(0.0, MDO_INFINITY, 1.0, "x1", MDO_NO));
        x.push_back(model.addVar(0.0, MDO_INFINITY, 1.0, "x2", MDO_NO));
        x.push_back(model.addVar(0.0, MDO_INFINITY, 1.0, "x3", MDO_NO));
        /* 添加约束 */
        model.addCons(1.0, MDO_INFINITY, 1.0 * x[0] + 1.0 * x[1] + 2.0 * x[2] + 3.0 * x[3], "c0");
        model.addCons(1.0, 1.0,          1.0 * x[0]              - 1.0 * x[2] + 6.0 * x[3], "c1");
        /* 添加二次目标矩阵 Q.
         * 1. 目标函数定义为c^Tx + 1/2 x^TQx，其中Q以坐标格式存储。
         * 2. Q 将在内部缩放 1/2。
         * 3. 为保证Q的对称性，用户只需输入下三角部分即可
         * Q = [ 1.0  0.5  0    0   ]
         *     [ 0.5  1.0  0    0   ]
         *     [ 0.0  0.0  1.0  0   ]
         *     [ 0    0    0    1.0 ]
        /*调用 mindopt::MdoModel::setQuadraticElements() 来设置目标的二次项系数 。
          前两组输入向量分别表示二次项中所有非零项的两个变量的索引，
          最后一组输入向量是与之相对应的非零系数值。*/
        model.setQuadraticElements
            { x[0], x[1], x[1], x[2], x[3] },
            { x[0], x[0], x[1], x[2], x[3] },
            {  1.0,  0.5,  1.0,  1.0,  1.0 }
        /*------------------------------------------------------------------*/
        /* Step 3.  解决问题并填充结果。               */
        /*------------------------------------------------------------------*/
        /* 调用 mindopt::MdoModel::solveProb() 求解优化问题，
           并通过 mindopt::MdoModel::displayResults() 查看优化结果 
        model.solveProb();
        model.displayResults();
    catch (MdoException & e)
        std::cerr << "===================================" << std::endl;
        std::cerr << "Error   : code <" << e.getResult() << ">" << std::endl;
        std::cerr << "Reason  : " << model.explainResult(e.getResult()) << std::endl;
        std::cerr << "===================================" << std::endl;
        return static_cast<int>(e.getResult());
    return static_cast<int>(MDO_OKAY);
}

MindOpt求解的结果

运行MdoQoEx1.cpp文件的步骤

linux和mac系统直接在命令行输入

cd <MDOHOME>/<VERSION>/examples/CPP
make -f Makefile all
./MdoQoEx1

windows系统本例是在 Visual Studio 上运行，版本为2019

#运行方式与前文一致，只需要修改文件就好；把MdoLoEx1.cpp换成MdoQoEx1.cpp

C++.gif

如上文所述，运行MdoMiloEx1.cpp文件，得到求解的结果如下所示，/**/号里面是我添加的注释。

Model summary.               /*模型摘要*/
 - Num. variables     : 4
 - Num. constraints   : 2
 - Num. nonzeros      : 7
 - Bound range        : [1.0e+00,1.0e+01]
 - Objective range    : [1.0e+00,1.0e+00]
 - Quad. obj. range   : [5.0e-01,1.0e+00]
 - Matrix range       : [1.0e+00,6.0e+00]
Presolver started.
Presolver terminated. Time : 0.001s
Interior point method started.   /*内点法*/
 Iter         PrimObj         DualObj PrimFea DualFea  GapFea      Mu   Time
    0 +5.21950421e+01 -5.93593455e+01 1.3e+00 8.0e-01 2.1e+00 1.5e+01   0.03s
    1 +5.75093325e+00 -3.28624247e+00 3.2e-02 2.0e-02 2.8e+00 1.5e+00   0.04s
    2 +1.19681205e+00 +1.03397025e-04 8.1e-04 3.7e-03 1.2e+00 2.0e-01   0.04s
    3 +6.52164783e-01 +3.52420863e-01 1.7e-04 3.7e-03 3.0e-01 4.9e-02   0.05s
    4 +4.65540318e-01 +4.35143347e-01 4.2e-06 9.3e-05 3.0e-02 5.1e-03   0.06s
    5 +4.40907312e-01 +4.39861230e-01 1.0e-07 2.3e-06 1.0e-03 1.7e-04   0.07s
    6 +4.40022716e-01 +4.39996554e-01 2.6e-09 5.8e-08 2.6e-05 4.4e-06   0.08s
    7 +4.40000569e-01 +4.39999914e-01 6.5e-11 1.5e-09 6.6e-07 1.1e-07   0.08s
    8 +4.40000014e-01 +4.39999998e-01 1.6e-12 3.7e-11 1.6e-08 2.7e-09   0.09s
    9 +4.40000000e-01 +4.40000000e-01 4.1e-14 9.1e-13 4.1e-10 6.9e-11   0.10s
Terminated.
 - Method             : Interior point method.
 - Primal objective   : 4.3999999966807E-01
 - Dual objective     : 4.3999999996074E-01
 - Num. threads       : 2
 - Num. iterations    : 9
 - Solver details     : Solver terminated with a primal/dual optimal status.
Interior point method terminated. Time : 0.107s
Optimizer summary.
 - Optimizer used     : Interior point method
 - Optimizer status   : OPTIMAL
 - Total time         : 0.116s
Solution summary.       Primal solution
 - Objective          : 4.3999999967e-01       /*目标函数最优解*/

联系我们

钉钉群号：32451444

邮箱地址：solver.damo@list.alibaba-inc.com

更多更新通知： https://solver.damo.alibaba.com

MindOpt-2023年度有奖问卷调研

MindOpt邀请您参与有奖问卷！

问卷填写地址： https://yida.alibaba-inc.com/o/MindOpt_2023
八个问题，预计耗时十分钟

联系小编个人钉账号领取奖品： hw2-wwffqg05p

电子邮箱联系： solver.damo@list.alibaba-inc.com

Visual Studio 2022 版本 17.4 预览版 3 中对c++编译时优化的内容你都知道吗

运筹优化学习09：一个示例带你入门如何使用C++、C#、Java、Python、Matlab调用Cplex（下）

运筹优化学习09：一个示例带你入门如何使用C++、C#、Java、Python、Matlab调用Cplex

运筹优化学习09：一个示例带你入门如何使用C++、C#、Java、Python、Matlab调用Cplex（上）