AI面试必刷算法题--持续更新

面试中发现很多同学一股脑优化、润色项目经历，但聊到基本的算法，反而会一脸懵X，得空整理下算法题给大家，希望对你有帮助。

1. tail(head(tail(C))) =( ) 已知广义表: A=(a,b), B=(A,A), C=(a,(b,A),B), 求下列运算的结果:（）

A 1000种量级

B 10000种量级

C 100000种量级

D 500000种以上

正确答案: C

不考虑失效的方式（就是不连贯的情况），那么如果9个点的话，排列组合有9！（362880）种，比9少的都达不到9的量级，在减去失效的也不会跨量级，所以是100000的量级。

2.线性表如果要频繁的执行插入和删除操作，该线性表采取的存储结构应该是（）

A 散列

B 顺序

C 链式

D 索引

正确答案: C

解析

D，索引结构，每次插入和删除都需要更新索引，费时 C，链式存储适合插入和删除操作

B，顺序存储插入和删除都需要移动大量元素

A，散列更适合查找，不适合频繁更新

答案：C

3.某段文本中各个字母出现的频率分别是{a:4，b:3，o:12，h:7，i:10}，使用哈夫曼编码，则哪种是可能的编码：（）

A a(001) b(000) h(01) i(10) o(11)

B a(0000) b(0001) h(001) o(01) i(1)

C a(000) b(001) h(01) i(10) o(00)

D a(0000) b(0001) h(001) o(000) i(1)

正确答案: A

首先：创建一个哈夫曼树

原则如下：

1. 将每个英文字母依照出现频率由小排到大，最小在左，组成一个序列

2. 每个字母都代表一个终端节点（叶节点），比较每个字母的出现频率，将最小的两个字母频率相加合成一个新的节点，将两个字母从序列中删除，将生成的节点加入到字母队列中

3. 重复前面两步，直到序列中没有字母为止

进行编码：

1. 给霍夫曼树的所有左链结'0'与右链结'1'

2. 从树根至树叶依序记录所有字母的编码

好：我们先来构造

v = ｛b(3)，a(4)，h(7),i(10),o(12)｝

取最小两个权值构成一棵树（如下）

--------（7）

---------/---\

-------/------\

-----b(3)---a(4)

然后将（7）加入序列：（7），h(7),i(10),o(12)

再取最小两个权值构成树：如下

-----------------(14)

--------------/--------\

------------/------------\

--------（7）---------h(7)

---------/---\

-------/------\

-----b(3)---a(4)

将（14）加入权值序列：（14）,i(10),o(12)

现在取10跟12构成一颗新数：如下

----------------(14)------------------(22)

--------------/--------\----------------/-----\

------------/------------\ -----------/----------\

--------（7）---------h(7) ---i(10)--------o(12)

---------/---\

-------/------\

-----b(3)---a(4)

最好权值相加:

--------------------------(36)

--------------------/-----------------\

------------------/---------------------\

----------------(14)------------------(22)

--------------/--------\----------------/-----\

------------/------------\ -----------/----------\

--------（7）---------h(7) ---i(10)--------o(12)

---------/---\

-------/------\

-----b(3)---a(4)

现在执行哈夫曼编码：从第二个接点开始：

进行编码：

1. 给霍夫曼树的所有左链结'0'与右链结'1'

2. 从树根至树叶依序记录所有字母的编码

--------------------------(36)

--------------------/-----------------\

------------------/---------------------\

----------------0(14)------------------1(22)

--------------/--------\----------------/-----\

------------/------------\ -----------/----------\

--------0（7）---------1h(7) ---0i(10)--------1o(12)

---------/---\

-------/------\

-----0b(3)---1a(4)

结果：a:001,b000,h01,i10,o11 选A

4.旅行商问题是NP问题吗？

A 否

B 是

正确答案: B

至今尚无定论旅行商问题是否NP问题

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论 的角度来看，该问题实质是在一个带权完全无向图 中，找一个权值最小的Hamilton 回路。由于该问题的可行解是所有顶点的全排列 ，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题 。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界 法、线性规划 法、动态规划 法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法 ，主要有遗传算法 、模拟退火法 、蚁群算法 、禁忌搜索 算法、贪婪算法 和神经网络等 。

5.下述编码中哪一个不是前缀码（）

A (00,01,10,11)

B (0,1,00,11)

C (0,10,110,111)

D (1,01,000,001)

正确答案: B

根据定义可知：B中有序列是另一个序列的前缀，可知错误

例如，{0,10,110}就是一个前缀码，而{0,10,101}就不是前缀码。

. 设Q ={a1, a2, …, am}是一个0~1序列集合 . 如果Q中没有一个序列是另一个序列的前缀 , 则称Q为前缀码。

6.一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和（）

A 对

B 错

正确答案: B

结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积。

树的带权路径长度(Weighted Path Length of Tree)：定义为树中所有叶结点的带权路径长度之和。

7.下列有关图的说法错误的是（）

正确答案: C

A 在有向图中,出度为0的结点称为叶子

B 用邻接矩阵表示图,容易判断任意两个结点之间是否有边相连,并求得各结点的度

C 按深度方向遍历图和前序遍历树类似,得到的结果是唯一的

D 若有向图G中从结点Vi到结点Vj有一条路径,则在图G的结点的线性序列中结点Vi,必在结点Vj之前的话,则称为一个拓扑序

8.下列关于线性表，二叉平衡树，哈希表存储数据的优劣描述错误的是？

正确答案: D

A 哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键 作为数组的索引。那么所有的查找时间复杂度为O(1)；

B 线性表实现相对比较简单

C 平衡二叉树的各项操作的时间复杂度为O（logn）

D 平衡二叉树的插入节点比较快

正确答案：D

哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)；如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。

在平衡二叉树中插入结点要随时保证插入后整棵二叉树是平衡的，所以可能需要通过一次或多次树旋转来重新平衡这个树推荐

9.在ASC算法team日常开发中，常常面临一些数据结构的抉择，令人纠结。目前大家在策划一个FBI项目（Fast Binary Indexing），其中用到的词汇有6200条，词汇长度在10-15之间，词汇字符是英文字母，区分大小写。请在下面几个数据结构中选择一个使检索速度最快的（）

A 二叉搜索树，比较函数开销：1次运算/每字符

B 哈希表，hash算法开销：10次运算/每字符

C 链表，比较函数开销：1次运算/每字符

D TRIE树，寻找子节点开销：1次运算/每字符

正确答案: D

注解:又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希表高。

10.下列陈述错误的是（ ）

A 数值概率算法一般是求数值计算问题的近似解

B Monte Carlo总能求得问题的一个解，但该解未必正确

C Las Vegas算法的一定能求出问题的正确解

D Sherwood算法的主要作用是减少或是消除好的和坏的实例之间的差别

正确答案: C

数值概率算法（数值问题的求解，最优化问题的近似解）、蒙特罗卡算法（判定问题的准确解，不一定正确）、拉斯维加斯算法（不一定会得到解，但得到的解一定是正确解）、舍伍德算法（总能求得一个解，且一定是正确解）

11.()的遍历仍需要栈的支持

A 前序线索树

B 中序线索树

C 后序线索树

正确答案: C

解析:

后序遍历要稍微复杂一点点，在前序和中序遍历的程序中，当我们准备进入根结点的右子树时，根结点就被扔出栈外了。但在后序遍历时，我们仍需保留它，直到右子树处理完毕。

12.关于 0 － 1 背包问题以下描述正确的是（ ）。

A 可以使用贪心算法找到最优解

B 能找到多项式时间的有效算法

C 使用教材介绍的动态规划方法可求解任意0－1背包问题

D 对于同一背包与相同的物品，做背包问题取得的总价值一定大于等于做0－1背包问题

正确答案: D

13.线性表若采用链式存储结构时，要求内存中可用存储单元的地址（）

A 必须是连续的

B 部分地址必须是联系的

C 一定是不连续的

D 连续或不连续都可以

正确答案: D

链表不需要存储空间连续，只需链表指针记录下一个地址即可。

14.设散列表中有 m 个存储单元，散列函数 H(key)= key % p ，则 p 最好选择（ ）

A 小于等于m的最大奇数

B 小于等于m的最大素数

C 小于等于m的最大偶数

B 小于等于m的最大素数

正确答案: B

15.已知模式串的 next 数组，使用 KMP 算法进行串匹配，以下空格应填入的语句是（ ）。

int Index_KMP(SString S, SString T, int pos)

{

// 利用模式串 T 的 next 函数求 T 在主串 S 中第 pos 个字符之后的位置的

// KMP 算法。其中， T 非空， 1 ≤ pos ≤ StrLength(S) 。

int next[255];

int i = pos;

int j = 1;

get_next(T, next);

while (i <= S[0] && j <= T[0]) {

if (j == 0 || S[i] == T[j]) { // 继续比较后继字符

++i; ++j;

} else

________; // 模式串向右移动

}

if (j > T[0]) return i-T[0]; // 匹配成功

else return 0;

} // Index_KMP

}

A j = next[j]

B i = next[j]

C j = i + 1

D i = j + 1

正确答案: A

解析：

KMP的算法流程是如下

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

• 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
• 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。
• 换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值，即 移动的实际位数为：j - next[j] ，且此值大于等于1。

很快，你也会意识到next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为 k 的相同前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

16.采用二叉链表作为存储结构,树的前序遍历和其相应的二叉树的前序遍历的结果是一样的（）

A 对

B 错

正确答案: A

解析：

树的二叉链表存储时，一个结点有两个指针域，一个指向它第一个孩子，一个指向它第一个兄弟。而将一般树转换为二叉树时，也是一个结点有一个结点有两个指针域，一个指向它第一个孩子，一个指向它第一个兄弟。

17. 下面关于求关键路径的说法不正确的是（）

A 求关键路径是以拓扑排序为基础的

B 一个事件的最早开始时间同以该事件为尾的弧的活动最早开始时间相同

C 一个事件的最迟开始时间为以该事件为尾的弧的活动最迟开始时间与该活动的持续时间的差

D 关键活动一定位于关键路径上

正确答案: C

做这题要注意几点概念：

1）顶点表示事件，弧表示活动

2）如果顶点A->B有弧，如果让弧表示为L，则A为L的弧尾，B为L的弧头，即有箭头的那一端叫头。

18. 解决哈希冲突的链地址算法中，关于插入新数据项的时间表述正确的是（）

A 和哈希表中项数成正比

B 和数组已占用单元的百分比成正比

C 随装载因子线性增长

D 和链表数目成正比

正确答案: C

19. 一个凸N边形，可以用N-3条互不相交的对角线将凸N边形分成N-2个三角形，这称为凸N边形的一种三角剖分。例如N＝5时，共有以下5种三角剖分（）

当N＝8时，总共有（）种三角剖分。

140

14

132

8

正确答案: B

多边形三角剖分公式

D(n+1)\Dn =(4n-6)\n (Dn表示凸n边形的三角剖分数）

D8=(D8\D7)*(D7\D6)*(D6\D5)=(22\7)*(3)*(14\5)=132

20.已知字符A、B、C、D的使用频率（权值）分别为22，7，9，27。对其进行HUFFMAN编码，各字符对应的编码为（ ）

A（001）B（100）C（110） D（0）

A（100） B（101）C（0） D（11）

A（11） B（100）C（101） D（0）

A（100）B（1011）C（11） D（0）

正确答案: C

21.能用二分法进行查找的是（）

A 顺序存储的有序线性表

B 线性链表

C 二叉链表

D 有序线性链表

正确答案: A

在计算机科学中，折半搜索，也称二分查找算法、二分搜索，是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

D. 有序线性链表不可以是因为链表的对结点的操作只能通过p->next的方式，对下标的操作不适合。

22.当一棵具有n个叶结点的二叉树的WPL值为最小时,称其树为哈夫曼树,且其二叉树的形状必是唯一的（）

对

错

正确答案: B

错误。应为二叉树中节点的左右子树是有序的。当根据n个叶结点的二叉树的WPL值最小构造树时，如果兄弟结点的权值相等，形状就不唯一了。

23.绳子对数轴各个点的覆盖

解析：

题目描述
数轴上从左到右有n个点a[0],a[1]...a[n-1],给定一根长度为L的绳子，求绳子最多能覆盖其中的几个点。

分析与解法
O(n^2)枚举自然都能能想到。

给个O(n)的想法。
以每个i为起点，只希望覆盖更多的点。
注意每次循环best和i都只增不减，尽管两个循环，复杂度还是O(n)的。
int calculate(int *a, int n, int L) {
int best = 0;
for (int i = 0; i + best < n; ++i) {
for (; (i + best < n) && (a[i + best] - a[i] <= L); ++best) ;
}
return best;
}

24.数组中子序列的个数

解析：

题目描述
给定一个数组a （可能包含相同的数），求它有多少个不同的子序列。
例如a={1,2,1,3}
子序列有 {1} {2} {3} {1,2} {1,3} {1,2} {1,1} {1,3} {2, 1} {2,3} {1,2,1} {1,2,3} {1,1,3} {2,1,3} 等。

分析与解法
这个题本身不难，但是分析清楚不容易。
我们首先假设子序列可以为空——最后减1就好了。

假设dp[i]表示数列前i项构成的不同子序列的个数。
初值：
dp[0] = 1 因为只有一个空子序列
我们现在考虑dp[i]
（1） 如果数列第i项在之前没有出现过，是一个新数
显然dp[i] = dp[i - 1] * 2
这是因为前(i-1)项的子序列本身，以及添加上第i项，都是一个子序列，这是比较容易的情况。如果全是这样，人生就完美了……因为我们会推出dp[i] = 2 ^ i， 但还有讨厌的第二种情况。
（2）如果第i项在之前出现过，假设j是它最近一次出现的位置，我们有0 < j < i （注意i,j都是项数，或者说下标从1开始的）
那么我们直接乘以2，有些会重复。哪些重复了呢？

原来的前(j-1)项的子序列末尾添加上第j项和添加上第i项是一样的，就这些是重复的。所以dp[j-1]是重复的。
此时 dp[i] = dp[i - 1] * 2 - dp[j - 1]
最后千万别忘记答案是dp[n] - 1因为我们考虑了空的子序列。
还有一种分析可以不考虑空的子序列，也是类似的。

25.两人取石子游戏

题目描述
Alice和Bob在玩一个取石子游戏，规则如下：
1，Alice先手，两人轮流取，每次可以取1/2/4颗。
2，取走最后一颗石子的人胜出。
问题：
1，共有16颗石子时，谁将胜出？
2，共有n (n>=1) 颗石子时，谁将胜出？

分析与解法
考虑Alice的必胜态：
当Alice取完本轮石子后，剩下的石子为3的倍数(3*n)，那么无论Bob怎么取，Alice都会赢。
简单解释如下：
①n = 1时，即Alice取完后只剩下3颗，那么无论Bob怎么取，Alice下次取都会取到最后一颗，会赢。
②n >1时，即Alice取完后剩下3*n颗，当Bob取完后，剩下的石子数量总可以表示为：
3*k+1 或 3*k + 2(k >= 0)，那么此时Alice可以将剩下的石子数重新变为3的倍数，如此递推下去。
...
最终剩下石子数量变为3。

也就是说，只要Alice取完后，剩下的石子数是3的倍数，那么Alice肯定会赢。
简单的C++实现代码如下：
//头文件 & 命名空间
include
using namespace std;//石子数为n时 判定谁赢void WhoWin(int n)
{
//Alice要先取
puts(n % 3 == 0? "Bob win" : "Alice win");
}

主函数
int main(void)
{
int n;
while(cin >> n)
{
WhoWin(n);
}
return 0;
}

26.RGB字符串的最短路径

解析：

题目描述
给一个字符串S，只包含R,G,B三种字符，起点在S[0]，目标走到S[n-1], n为S的长度
规则：
1) 每次可走若干步，但必须从R到G, G到B，B到R
2) 每走一次，需要代价 (j-i)*(j-i) (从i走到j)
问最小需要的cost, 如果不存在这样的路径，返回-1


分析与解法
例子：
RGGGB
0->2->4, 需要的cost= 2*2+2*2 = 8

解法一
其实这题就是一个最短路
如果i < j
(1) S[i] = 'R', S[j] = 'G', 建立一条(i - j) * (i - j) 的边
(2) S[i] = 'G',S[j] = 'B', 建立一条(i - j) * (i - j) 的边
(3) S[i] = 'B', S[j] = 'R', 建立一条(i - j) * (i - j)的边
求0到(n-1)的最短路。


解法二
当然 也可以动态规划
dp[x]表示到达x的最小代价
初值 dp[0] = 0
dp[j] = min(dp[i] + (i - j) * (i - j)) 如果i < j并且S[i] S[j]满足上面那个(1) (2) 或者(3)之一
求dp[n - 1]
其实两个方法是等价的……

27.寻找递增的三元组

解析：

题目描述
给定一个整数数组a, 希望判断下标三元组 i < j < k，满足a[i] < a[j] < a[k]。
是否可以用O(1)的空间，O(n)的时间找到一组？

分析与解法
解法一
O(n)时间 O(n)空间。
首先假设数组是a, 我们想找到这样3个index,比如3个index分别是i < j < k
我们看一下，当我们枚举j的时候，如果选取i和k? 一种可能是i选取a[0..j - 1]里面最小值的下标，而k选取a[j + 1..n - 1]最大值的下标。而这个东西我们可以用前缀、后缀的方法预处理出来。
比如我们可以算出b[i]表示 a[0..i]中最小值的下标，而c[i]表示a[i..n - 1]中最大值的下标。这个可以循环处理。
for (int i = 0; i < n; ++i)
{
b[i] = ((i == 0) || (a[b[i - 1]] > a[i]))? i : b[i - 1];
}
for (int i = n - 1; i >= 0; --i)
{
c[i] = ((i == n - 1) || (a[c[i + 1]] < a[i]))? i : c[i + 1];
}
这样,选取的时候对i我们直接看一下b[i - 1]和c[i + 1]就可以了。
for (int i = 1; i + 1 < n; ++i)
{
if ((a[b[i - 1]] < a[i]) && (a[c[i + 1]] > a[i]))
{
return b[i - 1], i , c[i + 1]是一个解
}
}


解法二
O(n)时间，O(1)空间的算法。
利用LIS的思想，因为我们实际上就是要找到一个长度为3的单调子序列，那么我们可以用O(nlogn)的LIS思想，但是由于长度只维护到3，所以没有必要2分，而且没有必要用数组保存长度为x的单调子序列的最后一项的最小值，用变量存就好了，但思路是不变的。

我们这么记录x表示目前为止长度为1的单增子序列最后一项的最小值在数组a中的下标，实际上x就是我们刚才那个b数组，而y表示目前为止长度为2的单增子序列最后一项的最小值在数组a中的下标。

根据单调子序列的性质，我们有a[x] < a[y], 这个其实就是那个O(nlogn)算法思想的核心。我们先让x = 0,让y = -1，表示目前长度为1的单增自序列就是第一项，没有长度为2的单增子序列。

同时我们需要维护一个z，表示长度为2的单增自序列的首项，也就是y之前那一项。我们从i = 1开始维护x、y、z的值。
y = -1时a[y]定义为无穷大。 我们看一下a[i] 和a[x] a[y]的关系。 (注意始终有a[x] a[y]，则我们找到了三元组(z, y, i)满足条件
（2） 如果a[i] == a[y]， 则这一项没有意义，无法扩展子序列
（3） 如果a[x] < a[i] < a[y] (当然我们可以把情况2也放到这里）， 那么我们可以把长度为2的单调子序列最后一项更新一下，所以更新y = i, z = x，实际上a[x], a[i]是个长度为2的单增子序列，且最后一项比a[y]小。
（4） 如果a[i] == a[x], 则这一项没有意义， 无法扩展子序列
（5） 如果a[i] < a[x] (当然我们可以把情况4也放到这里）， 那么我们可以把长度为1的单调子序列最后一项更新一下（也就是目前最小值），所以更新x = i

这个时间复杂度显然是O(n)，空间复杂度是O(1)。
int x = 0;int y = -1;int z = -1;for (int i = 1; i < n; ++i)
{
if ((y >= 0) && (a[i] > a[y]))
{
return 找到三元组(z, y, i)满足要求
}
else if (a[i] > a[x])
{
y = i;
z = x;
}
else
{
x = i;
}
}

28.储油点的最佳配置

解析：

题目描述
一个环形跑道上有若干个储油点。储油点油的总量刚好够一辆汽车走完一圈。假设汽车是均匀耗油的，并且油箱足够大，初始为空。它可以选择一个储油点为起点，装好油沿着环形跑道走下去，每到一个储油点，就可以装上那里的油。问是否可以选择这样一个的起点使得让汽车走完一圈回到起点。


分析与解法
如果把每个储油点的油量减去到下一个储油点的耗油量当成一个变量a[i]，则我们有
a[1] + a[2] + ... + a[n] = 0 因为全部油刚好够一圈，问题是这个有正有负数。

我们假设A = a[1] + a[2] + ... + a[k - 1]是前缀的最小值，并且假设A<0,因为如果A>=0，则从第一个储油点开始走，不会出现负数，这个储油点就是解了。

我们令B=a[k] + a[k + 1] + ... + a[n], 则B = -A >= 0
我们考虑 B的每个前缀
a[k], a[k] + a[k + 1], a[k] + a[k + 1] + a[k + 2],....,B, 这些前缀必须都是非负数，因为如果前缀有一个负数的x的话，从a[1]开始的前缀和A + x < A，与A最小矛盾。

我们再继续
B + a[1], B + a[1] + a[2], ..... B + A
因为从B开始加的那部分就是从a[1]开始的前缀，我们知道A是最小的，所以这串数的最小值是A + B = 0，这就证明了从a[k]开始出发，加出来的数不会出现负数。所以k是一个解。

我们这个算法的时间复杂度是O(n)，因为我们只需要自己加一次把和最小的位置找出来就可以了。
另外，我们其实并没有规定顺时针还有逆时针行走，所以可以分别考虑求出不同方向行驶的出发点。

29.字符串到整数的映射

解析：

题目描述
某Hash函数将任一字符串非均匀映射到正整数k，概率为2^(-k)，即：P{Hash()=k}=2^(-k)。
现有字符串集合S，其元素经映射后，得到的最大整数为10。试估计S的元素个数。
提示：被映射得到的整数快速衰减，“最大整数为10”这一条件可近似考虑为“存在某整数为10”。


分析与解法
（某Hash函数将任一字符串非均匀映射到正整数k，概率为2-k，如下所示。现有字符串集合S，其元素经映射后，得到的最大整数为10。试估计S的元素个数。

）
问题分析：
由于Hash映射成整数是指数级衰减的，“最大整数为10”这一条件可近似考虑成“整数10曾经出现”，继续近似成“整数10出现过一次”。
字符串被映射成10的概率为p=2-10=1/1024，从而，一次映射即两点分布：

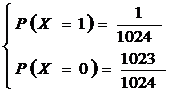
从而n个字符串的映射，即二项分布：

二项分布的期望为：

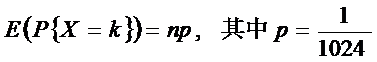
而期望表示n次事件发生的次数，当前问题中发生了1次，从而：

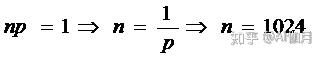
30.质因数的分解

解析：

题目描述
给定一个整数x， 满足|x| > 1，求满足条件的整数a, b使得x = a^b (a的b次方), 显然b最小为1，因为a= x, b =1是一组可能的解。请求出最大可能的b。
函数签名 int maxPower(int x);

分析与解法
简单来说，就是对x做质因数分解。
把x写成pk11pk22⋯pknn

那么k1,k2,⋯,kn的最大公约数就是对于x来说最大的可能的b。也即
x=(pk1b1pk2b2⋯pknbn)b
int maxPower(int x)
{
int a = abs(x);
std::map pf; //计算x的绝对值的质因数分解
for (int i = 2; i <= a / i; i++)
{
while (a % i == 0)
{
pf[i]++;
a /= i;
}
}
if (a > 1) pf[a]++;
int mp = 32; //int长度表示整数为-2^31 - 2^31-1，所以mp最大为32
for (; mp >= 1; mp--) //计算质因数分解中所有指数的最大公约数
{
bool valid = true;
for (auto it = pf.begin(); it != pf.end(); ++it)
{
if (it->second % mp != 0)
{
valid = false;
break;
}
}
if (valid && (x > 0 || mp % 2 == 1)) //当x为负值时，需要保证mp为奇数
break;
}
return mp;
}

31.在一个严格单调递增的整数数组中找到a[x] == x的位置？

解析：

分析与解法
设整数x1>x2，并且有x1=x2+d。由于数组a是一个严格单调递增的整数数组，所以必然有a[x1]⩾a[x2]+d。
两边同时减去x1，即a[x1]−x1⩾a[x2]+d−x2−d=a[x2]−x2。所以f(x)=a[x]−x 也是一个单调递增的函数。

那么原问题寻找a[x]=x的位置也就变成了查找单调递增函数f(x)=0时对应的x。这样就可以直接使用二分查找来做了，时间复杂度为O(logn)
void find(int a[], int l, int r)
{
if (l > r)
return -1;
int k = (l + r) / 2;
if (a[k] == k)
return k;
else if (a[k] > k)
return find(a, l, k - 1);
else
return find(a, k + 1, r);
}

32.机器人行走路径

解析：

题目描述
二维平面上有一个机器人，初始面朝北(N)。有一个字符串代表它的指令序列commend，它只包含4种字符,LRFB。表示朝左转90度、朝右转90度，前进一个单位和退后一个单位。但是机器人是循环执行指令的，即执行完这个字符串后，再从第一个字符开始再执行一次，如此下去，不断执行。
问机器人运动的轨迹（无限运动）是否是有限的？ 即是否有一个足够大的圆可以包围机器人所能走到的区域？


分析与解法
连续模拟那个commend 至多5次，必然有两次朝向一样的，分析这两次，实际上有一个位移，如果这个位移是0，说明他在转圈，否则就相当于它不断沿着这个向量方向再走，直到无穷远……

33.Two Sum

解析：

题目描述
给定一个整数sum,从有N个有序元素的数组中寻找元素a,b,使得a+b的结果最接近sum,最快的平均时间复杂度是多少？


分析与解法
答案：O(n)
思想类似于两端向中间扫描
1、设定两个指针P1、P2，分别指向数组开始和结尾，即P1指向最小值，P2指向最大值；
2、计算 *P1+*P2 的值为 SUM，与 sum 比较，记录它们的差值 DIF 和 SUM，若 SUM < sum，P1++，若 SUM > sum，P2--;
3、重复以上过程直到DIF最小

但如果数组是无序的呢？
如果数组是无序的，先排序（n*logn），然后用两个指针i，j，各自指向数组的首尾两端，令i=0，j=n-1，然后i++，j--，逐次判断a[i]+a[j]?=sum，如果某一刻a[i]+a[j]>sum，则要想办法让sum的值减小，所以此刻i不动，j--，如果某一刻a[i]+a[j] < sum，则要想办法让sum的值增大，所以此刻i++，j不动。所以，数组无序的时候，时间复杂度最终为O（n*logn+n）=O（n*logn）。

当然，如果原数组是有序的，则不需要事先的排序，直接O（n）搞定，且空间复杂度还是O（1）。
所以，如果有序，直接两个指针两端扫描，时间O（N），如果无序，先排序后两端扫描，时间O（N*logN+N）=O（N*logN），空间始终都为O（1）。

换言之，不论原序列是有序还是无序，解决这类题有以下三种办法：
1、对每个a[i]，二分查找sum-a[i]是否也在原始序列中，若无序，则先排序后二分，时间复杂度总为O（n*logn），空间复杂度为O（1）；
2、扫描一遍X-S[i] 映射到一个数组或构造hash表，时间复杂度为O（n），空间复杂度为O（n）；
3、两个指针两端扫描（若无序，先排序后扫描），时间复杂度最后为：有序O（n），无序O（n*logn+n）=O（n*logn），空间复杂度都为O（1）。
所以，要想达到时间O（N），空间O（1）的目标，除非原数组是有序的（指针扫描法），不然，当数组无序的话，就只能先排序，后指针扫描法或二分（时间n*logn，空间O（1）），或映射或hash（时间O（n），空间O（n））。时间或空间，必须牺牲一个，自个权衡。

综上，若是数组有序的情况下，优先考虑两个指针两端扫描法，以达到最佳的时（O（N）），空（O（1））效应。否则，如果要排序的话，时间复杂度最快当然是只能达到N*logN，空间O（1）则是不在话下。

//代码一
//O（N）
Pair findSum(int *s,int n,int x)
{
//sort(s,s+n); 如果数组非有序的，那就事先排好序O（N*logN）

int *begin=s;
int *end=s+n-1;

while(begin < end) //俩头夹逼，或称两个指针两端扫描法，很经典的方法，O（N）
{
if(*begin+*end>x)
{
--end;
}
else if(*begin+*end < x)
{
++begin;
}
else
{
return Pair(*begin,*end);
}
}

return Pair(-1,-1);
}

//或者如下编写，
//代码二
//copyright@ zhedahht && yansha
//July、updated，2011.05.14。
bool find_num(int data[], unsigned int length, int sum, int& first_num, int& second_num)
{
if(length < 1)
return true;

int begin = 0;
int end = length - 1;

while(end > begin)
{
long current_sum = data[begin] + data[end];

if(current_sum == sum)
{
first_num = data[begin];
second_num = data[end];
return true;
}
else if(current_sum > sum)
end--;
else
begin++;
}
return false;
}

34.二分查找的实现

解析：

题目描述
下面是折半查找的实现，data是按升序排列的数据，x是查找下标，y是查找的上标，
v是查找的数值，返回v在data的索引，若没找到返回-1。代码不正确是____。

分析与解法
解析：上下标没有写清楚，题目所指的应该是[x,y),这样5应该是m-1
而在下标为[x,y]的情况下，1,4,5都是有问题的。。。。正确版本应该是这样吧
while(x<=y) {
m = x + (y-x)/2; //2
if(data[m] == v) return m; //3
else if(data[m] > v) y = m-1; //4
else x = m+1; //5
}

补充：这里下标是个坑，记住上限有没有包含就可以对付1,4,5处的问题（熟记理解两个版本的代码区别），然后是2，写成x+(y-x)/2是防止xy都很大的情况下x+y越界。这样的话应对二分查找应该够了

35.有序数组的查找(二分查找)

解析：

题目描述
给定一个排好序的数组，查找某个数是否在这个数组中，请编程实现。


分析与解法
一看到数组本身已经有序，直观的反应可能是用二分查找算法，毕竟二分查找算法的适用条件就是要求数组是有序的。那么什么是二分查找呢？

二分查找可以解决已排序数组的查找的问题，即只要数组中包含 T（要查找的值），那么通过不断缩小包含T的数据范围，就可以最终找到要找的数T。其算法流程如下。

（1）一开始，数据范围覆盖整个数组。
（2）将数组的中间项与T进行比较，如果T比数组的中间项小，则到数组的前半部分继续查找，反之，则到数组的后半部分继续查找。
（3）这样，每次查找都可以排除一半元素，相当于范围缩小一半。这样反复比较，反复缩小范围，最终会在数组中找到T，或者确定T不在此数组中。

对于包含n个元素的数组，整个查找过程大约要经过log n次比较。

此时，可能有读者心里想，不就二分查找嘛，太简单了。但是，《编程珠玑》的作者Jon Bentley曾在贝尔实验室做过一个实验，即给一些专业的程序员几个小时的时间，用任何一种语言编写二分查找的程序（写高级伪代码也可以），结果参与编写的一百多个人中，90%的程序员写的程序中有bug（没发现bug的代码不代表就正确）。也就是说，在足够的时间内，只有大约10%的专业程序员可以把二分查找写对。此外，高德纳在《计算机程序设计的艺术 第3卷：排序和查找》的6.2.1节的“历史与参考文献”中指出，虽然早在1946年就有人将二分查找的方法公诸于世，但直到1962年才有人写出没有bug的二分查找程序。

实际上，要想编写出正确的二分查找程序，必须注意到两点：一点是判断循环体是否终止的语句的编写，另外一点是边界值left、right和区间值这三个地方要保持一致。

关于第二点再详细说明一下。例如，如果令right=n−1，则while循环的循环条件为left <= right，从而更新右边界位置的时候为right=middle−1；而如果令right=n，则while循环的循环条件为left < right，从而更新右边界位置的时候为right=middle。同时，middle的计算不能写在while循环外，否则无法得到更新。

以下是一份参考实现：

int BinarySearch(int array[], int n, int value)
{
int left = 0;
int right = n - 1;
// 如果上面这句是int right = n的话，则下面有两处地方需要修改，以保证一一对应：
// 1. 循环的条件是while(left < right)；
// 2. 循环内，当array[middle] > value的时候，right = mid。

while (left <= right) // 循环条件，适时而变
{
// 求中间位置，使用移位的方法是为了防止溢出，同时也更高效。注意，每次循环都需要更新
int middle = left + ((right - left) >> 1);
if (array[middle] > value)
{
right = middle - 1; // right赋值，适时而变
}
else if (array[middle] < value)
{
left = middle + 1;
}
else
{
// 可能会有读者认为刚开始时就要判断相等，但其实无关紧要，毕竟数组中不相等的情况更多
return middle;
}
}
return -1;
}

36.音乐播放器的随机播放

解析：

题目描述
假设张三的mp3里有1000首歌，现在希望设计一种随机算法来随机播放。与普通随机模式不同的是，张三希望每首歌被随机到的概率是与一首歌的豆瓣评分（0~10分）成正比的，如朴树的《平凡之路》评分为8.9分，逃跑计划的《夜空中最亮的星》评分为9.5分，则希望听《平凡之路》的概率与《夜空中最亮的星》的概率比为89:95。

现在我们已知这1000首歌的豆瓣评分：
（1）请设计一种随机算法来满足张三的需求。
（2）写代码实现自己的算法。


分析与解法
#include
#include
#include
using namespace std;

int findIdx(double songs[],int n,double rnd){
int left=0;
int right=n-1;
int mid;
while(left<=right){
mid=(left+right)/2;
if((songs[mid-1]<=rnd) && (songs[mid]>=rnd))
return mid;
if(songs[mid]>rnd)
right=mid-1;
else
left=mid+1;
}
// return mid;
}

int randomPlaySong(double sum_scores[],int n){
double mx=sum_scores[n-1];
double rnd= rand()*mx/(double)(RAND_MAX);
return findIdx(sum_scores,n,rnd);
}

int main()
{
srand(time(0));
double scores[]={5.5,6.5,4.5,8.5,9.5,7.5,3.5,5.0,8.0,2.0};
int n=sizeof(scores)/sizeof(scores[0]);
double sum_scores[n];
sum_scores[0]=scores[0];

for(int i=1;i

37.最小分割数

解析：

题目描述
给 n 个正整数 a_1,…,a_n， 将 n 个数顺序排成一列后分割成 m 段，每一段的分数被记为这段内所有数的和，该次分割的分数被记为 m 段分数的最大值。问所有分割方案中分割分数的最小值是多少？

输入描述：
第一行依次给出正整数 n, m。
第二行依次给出n 个正整数 a1,...,ana1,...,an。

示例：

输入
5 3
1 4 2 3 5
输出
5
说明
分割成 1 4 | 2 3 | 5 的时候三段的分数都为 5，得到分割分数的最小值。

备注：
对于所有的数据，有 m <= n <= 100000,0 <= aiai <= 2^39。


分析与解法
将 n 个数划分为 n 段，分割分数即为 n 个正整数的最大值；
将 n 个数划分为 1 段，分割分数即为 n 个正整数的和；
若分为 m 段，则分割分数一定介于最大值与和之间。因此采用二分查找，每次取一个值对序列进行划分，若能划分出
m 段，使得每段的和都小于这个数值，则满足划分，反之不满足，直至找到一个最小的满足划分的值为止。

代码实现如下：

#include
using namespace std;

int Judge(int data[], int sum, int m, int n);
int Binary_Search(int data[], int left, int right, int m, int n);


int main()
{
int n = 0, m = 0;
cin >> n >> m;

int data[n];
int max_num = 0;
int sum = 0;

int i = 0;

for(i = 0; i < n ; i++)
{
cin >> data[i];
if (data[i] > max_num)
{
max_num = data[i];
}
sum += data[i];
}

cout << Binary_Search(data, max_num, sum, m, n);

return 0;
}

int Binary_Search(int data[], int left, int right, int m, int n)
{
int mid = 0;

while (left < right)
{
mid = left + (right - left) / 2;
if (Judge(data, mid, m, n)) //满足划分，继续向左寻找
{
right = mid;//不减是因为无法确保减一之后的数是否满足划分
}
else //不满足划分，继续向右寻找
{
left = mid + 1;
}
}

return left;
}

int Judge(int data[], int mid, int m, int n)
{
int cnt = 0;
int sum = 0;

for (int i = 0; i < n; i++)
{
if (sum + data[i] > mid) //累加和大于 mid，进行一次划分
{
sum = data[i];
cnt++;
if (cnt > m - 1) //划分次数大于 m-1,不满足划分
{
return 0;
}
}
else
{
sum += data[i];
}
}

return 1;
}

38.最长回文子串

解析：

题目描述
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1：
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：
输入: "cbbd"
输出: "bb"


分析与解法
最容易想到的办法是枚举所有的子串，分别判断其是否为回文。这个思路初看起来是正确的，但却做了很多无用功，如果一个长的子串包含另一个短一些的子串，那么对子串的回文判断其实是不需要的。

解法一

那么如何高效的进行判断呢？我们想想，如果一段字符串是回文，那么以某个字符为中心的前缀和后缀都是相同的，例如以一段回文串“aba”为例，以b为中心，它的前缀和后缀都是相同的，都是a。

那么，我们是否可以可以枚举中心位置，然后再在该位置上用扩展法，记录并更新得到的最长的回文长度呢？答案是肯定的，参考代码如下：

int LongestPalindrome(const char *s, int n)
{
int i, j, max,c;
if (s == 0 || n < 1)
return 0;
max = 0;

for (i = 0; i < n; ++i) { // i is the middle point of the palindrome
for (j = 0; (i - j >= 0) && (i + j < n); ++j){ // if the length of the palindrome is odd
if (s[i - j] != s[i + j])
break;
c = j * 2 + 1;
}
if (c > max)
max = c;
for (j = 0; (i - j >= 0) && (i + j + 1 < n); ++j){ // for the even case
if (s[i - j] != s[i + j + 1])
break;
c = j * 2 + 2;
}
if (c > max)
max = c;
}
return max;
}
代码稍微难懂一点的地方就是内层的两个 for 循环，它们分别对于以 i 为中心的，长度为奇数和偶数的两种情况，整个代码遍历中心位置 i 并以之扩展，找出最长的回文。

解法二、O(N)解法

在上文的解法一：枚举中心位置中，我们需要特别考虑字符串的长度是奇数还是偶数，所以导致我们在编写代码实现的时候要把奇数和偶数的情况分开编写，是否有一种方法，可以不用管长度是奇数还是偶数，而统一处理呢？比如是否能把所有的情况全部转换为奇数处理？

答案还是肯定的。这就是下面我们将要看到的Manacher算法，且这个算法求最长回文子串的时间复杂度是线性O(N)的。

首先通过在每个字符的两边都插入一个特殊的符号，将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。

此外，为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

以字符串12212321为例，插入#和$这两个特殊符号，变成了 S[] = "$#1#2#2#1#2#3#2#1#"，然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左或向右扩张的长度（包括S[i]）。

比如S和P的对应关系：

S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
可以看出，P[i]-1正好是原字符串中最长回文串的总长度，为5。

接下来怎么计算P[i]呢？Manacher算法增加两个辅助变量id和mx，其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。得到一个很重要的结论：

如果mx > i，那么P[i] >= Min(P[2 * id - i], mx - i)
C代码如下：

//mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)
//故谁小取谁
if (mx - i > P[2*id - i])
P[i] = P[2*id - i];
else //mx-i <= P[2*id - i]
P[i] = mx - i;
下面，令j = 2*id - i，也就是说j是i关于id的对称点。

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于i和j对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有P[i] = P[j]；

当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，再具体匹配。

此外，对于 mx <= i 的情况，因为无法对 P[i]做更多的假设，只能让P[i] = 1，然后再去匹配。

综上，关键代码如下：

//输入，并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++)
{
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
while (s[i + p[i]] == s[i - p[i]])
p[i]++;
if (i + p[i] > mx)
{
mx = i + p[i];
id = i;
}
}
//找出p[i]中最大的
此Manacher算法使用id、mx做配合，可以在每次循环中，直接对P[i]的快速赋值，从而在计算以i为中心的回文子串的过程中，不必每次都从1开始比较，减少了比较次数，最终使得求解最长回文子串的长度达到线性O(N)的时间复杂度。

参考： http://www. felix021.com/blog/read. php?2040 。另外，这篇文章也不错： http:// leetcode.com/2011/11/lo ngest-palindromic-substring-part-ii.html 。

39.字符串包含

解析：

题目描述
给定两个分别由字母组成的字符串A和字符串B，字符串B的长度比字符串A短。请问，如何最快地判断字符串B中所有字母是否都在字符串A里？

为了简单起见，我们规定输入的字符串只包含大写英文字母，请实现函数bool StringContains(string &A, string &B)

比如，如果是下面两个字符串：
String 1：ABCD
String 2：BAD
答案是true，即String2里的字母在String1里也都有，或者说String2是String1的真子集。

如果是下面两个字符串：
String 1：ABCD
String 2：BCE
答案是false，因为字符串String2里的E字母不在字符串String1里。

同时，如果string1：ABCD，string 2：AA，同样返回true。


分析与解法
题目描述虽长，但题意很明了，就是给定一长一短的两个字符串A，B，假设A长B短，要求判断B是否包含在字符串A中。

初看似乎简单，但实现起来并不轻松，且如果面试官步步紧逼，一个一个否决你能想到的方法，要你给出更好、最好的方案时，恐怕就要伤不少脑筋了。

解法一

判断string2中的字符是否在string1中?最直观也是最简单的思路是，针对string2中每一个字符，逐个与string1中每个字符比较，看它是否在String1中。

代码可如下编写：

bool StringContain(string &a,string &b)
{
for (int i = 0; i < b.length(); ++i) {
int j;
for (j = 0; (j < a.length()) && (a[j] != b[i]); ++j)
;
if (j >= a.length())
{
return false;
}
}
return true;
}
假设n是字符串String1的长度，m是字符串String2的长度，那么此算法，需要O(n*m)次操作。显然，时间开销太大，应该找到一种更好的办法。

解法二

如果允许排序的话，我们可以考虑下排序。比如可先对这两个字符串的字母进行排序，然后再同时对两个字串依次轮询。两个字串的排序需要(常规情况)O(m log m) + O(n log n)次操作，之后的线性扫描需要O(m+n)次操作。

关于排序方法，可采用最常用的快速排序，参考代码如下：

//注意A B中可能包含重复字符，所以注意A下标不要轻易移动。这种方法改变了字符串。如不想改变请自己复制
bool StringContain(string &a,string &b)
{
sort(a.begin(),a.end());
sort(b.begin(),b.end());
for (int pa = 0, pb = 0; pb < b.length();)
{
while ((pa < a.length()) && (a[pa] < b[pb]))
{
++pa;
}
if ((pa >= a.length()) || (a[pa] > b[pb]))
{
return false;
}
//a[pa] == b[pb]
++pb;
}
return true;
}
解法三

有没有比快速排序更好的方法呢？

我们换一种角度思考本问题：

假设有一个仅由字母组成字串，让每个字母与一个素数对应，从2开始，往后类推，A对应2，B对应3，C对应5，......。遍历第一个字串，把每个字母对应素数相乘。最终会得到一个整数。

利用上面字母和素数的对应关系，对应第二个字符串中的字母，然后轮询，用每个字母对应的素数除前面得到的整数。如果结果有余数，说明结果为false。如果整个过程中没有余数，则说明第二个字符串是第一个的子集了（判断是不是真子集，可以比较两个字符串对应的素数乘积，若相等则不是真子集）。

思路总结如下：

按照从小到大的顺序，用26个素数分别与字符'A'到'Z'一一对应。
遍历长字符串，求得每个字符对应素数的乘积。
遍历短字符串，判断乘积能否被短字符串中的字符对应的素数整除。
输出结果。
如前所述，算法的时间复杂度为O(m+n)的最好的情况为O(n)（遍历短的字符串的第一个数，与长字符串素数的乘积相除，即出现余数，便可退出程序，返回false），n为长字串的长度，空间复杂度为O(1)。

//此方法只有理论意义，因为整数乘积很大，有溢出风险
bool StringContain(string &a,string &b)
{
const int p[26] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,61, 67, 71, 73, 79, 83, 89, 97, 101};
int f = 1;
for (int i = 0; i < a.length(); ++i)
{
int x = p[a[i] - 'A'];
if (f % x)
{
f *= x;
}
}
for (int i = 0; i < b.length(); ++i)
{
int x = p[b[i] - 'A'];
if (f % x)
{
return false;
}
}
return true;
}
此种素数相乘的方法看似完美，但缺点是素数相乘的结果容易导致整数溢出。

解法四

如果面试官继续追问，还有没有更好的办法呢？计数排序？除了计数排序呢？

事实上，可以先把长字符串a中的所有字符都放入一个Hashtable里，然后轮询短字符串b，看短字符串b的每个字符是否都在Hashtable里，如果都存在，说明长字符串a包含短字符串b，否则，说明不包含。

再进一步，我们可以对字符串A，用位运算（26bit整数表示)计算出一个“签名”，再用B中的字符到A里面进行查找。

// “最好的方法”，时间复杂度O(n + m)，空间复杂度O(1)
bool StringContain(string &a,string &b)
{
int hash = 0;
for (int i = 0; i < a.length(); ++i)
{
hash |= (1 << (a[i] - 'A'));
}
for (int i = 0; i < b.length(); ++i)
{
if ((hash & (1 << (b[i] - 'A'))) == 0)
{
return false;
}
}
return true;
}
这个方法的实质是用一个整数代替了hashtable，空间复杂度为O(1)，时间复杂度还是O(n + m)。

举一反三

1、变位词

如果两个字符串的字符一样，但是顺序不一样，被认为是兄弟字符串，比如bad和adb即为兄弟字符串，现提供一个字符串，如何在字典中迅速找到它的兄弟字符串，请描述数据结构和查询过程。

40.字符串转换成整数

解析：

题目描述
输入一个由数字组成的字符串，把它转换成整数并输出。例如：输入字符串"123"，输出整数123。
给定函数原型int StrToInt(const char *str) ，实现字符串转换成整数的功能，不能使用库函数atoi。


分析与解法
本题考查的实际上就是字符串转换成整数的问题，或者说是要你自行实现atoi函数。那如何实现把表示整数的字符串正确地转换成整数呢？以"123"作为例子：

当我们扫描到字符串的第一个字符'1'时，由于我们知道这是第一位，所以得到数字1。
当扫描到第二个数字'2'时，而之前我们知道前面有一个1，所以便在后面加上一个数字2，那前面的1相当于10，因此得到数字：1*10+2=12。
继续扫描到字符'3'，'3'的前面已经有了12，由于前面的12相当于120，加上后面扫描到的3，最终得到的数是：12*10+3=123。
因此，此题的基本思路便是：从左至右扫描字符串，把之前得到的数字乘以10，再加上当前字符表示的数字。

思路有了，你可能不假思索，写下如下代码：

int StrToInt(const char *str)
{
int n = 0;
while (*str != 0)
{
int c = *str - '0';
n = n * 10 + c;
++str;
}
return n;
}
显然，上述代码忽略了以下细节：

空指针输入：输入的是指针，在访问空指针时程序会崩溃，因此在使用指针之前需要先判断指针是否为空。
正负符号：整数不仅包含数字，还有可能是以'+'或'-'开头表示正负整数，因此如果第一个字符是'-'号，则要把得到的整数转换成负整数。
非法字符：输入的字符串中可能含有不是数字的字符。因此，每当碰到这些非法的字符，程序应停止转换。
整型溢出：输入的数字是以字符串的形式输入，因此输入一个很长的字符串将可能导致溢出。
上述其它问题比较好处理，但溢出问题比较麻烦，所以咱们来重点看下溢出问题。

一般说来，当发生溢出时，取最大或最小的int值。即大于正整数能表示的范围时返回MAX_INT：2147483647；小于负整数能表示的范围时返回MIN_INT：-2147483648。

我们先设置一些变量：

sign用来处理数字的正负，当为正时sign > 0，当为负时sign < 0
n存放最终转换后的结果
c表示当前数字
而后，你可能会编写如下代码段处理溢出问题：

//当发生正溢出时，返回INT_MAX
if ((sign == '+') && (c > MAX_INT - n * 10))
{

n = MAX_INT;
break;
}
//发生负溢出时，返回INT_MIN
else if ((sign == '-') && (c - 1 > MAX_INT - n * 10))
{
n = MIN_INT;
break;
}
但当上述代码转换" 10522545459"会出错，因为正常的话理应得到MAX_INT：2147483647，但程序运行结果将会是：1932610867。

为什么呢？因为当给定字符串" 10522545459"时，而MAX_INT是2147483647，即MAX_INT(2147483647) < n*10(1052254545*10)，所以当扫描到最后一个字符‘9’的时候，执行上面的这行代码：

c > MAX_INT - n * 10
已无意义，因为此时(MAX_INT - n * 10)已经小于0，程序已经出错。

针对这种由于输入了一个很大的数字转换之后会超过能够表示的最大的整数而导致的溢出情况，我们有两种处理方式可以选择：

一个取巧的方式是把转换后返回的值n定义成long long，即long long n；
另外一种则是只比较n和MAX_INT / 10的大小，即：
若n > MAX_INT / 10，那么说明最后一步转换时，n*10必定大于MAX_INT，所以在得知n > MAX_INT / 10时，当即返回MAX_INT。
若n == MAX_INT / 10时，那么比较最后一个数字c跟MAX_INT % 10的大小，即如果n == MAX_INT / 10且c > MAX_INT % 10，则照样返回MAX_INT。
对于上面第一种方式，虽然我们把n定义了长整型，但最后返回时系统会自动转换成整型。咱们下面主要来看第二种处理方式。

对于上面第二种方式，先举两个例子说明下：

如果我们要转换的字符串是"2147483697"，那么当我扫描到字符'9'时，判断出214748369 > MAX_INT / 10 = 2147483647 / 10 = 214748364（C语言里，整数相除自动取整，不留小数），则返回MAX_INT；
如果我们要转换的字符串是"2147483648"，那么判断最后一个字符'8'所代表的数字8与MAX_INT % 10 = 7的大小，前者大，依然返回MAX_INT。
一直以来，我们努力的目的归根结底是为了更好的处理溢出，但上述第二种处理方式考虑到直接计算n * 10 + c 可能会大于MAX_INT导致溢出，那么便两边同时除以10，只比较n和MAX_INT / 10的大小，从而巧妙的规避了计算n*10这一乘法步骤，转换成计算除法MAX_INT/10代替，不能不说此法颇妙。

如此我们可以写出正确的处理溢出的代码：

c = *str - '0';
if (sign > 0 && (n > MAX_INT / 10 || (n == MAX_INT / 10 && c > MAX_INT % 10)))
{
n = MAX_INT;
break;
}
else if (sign < 0 && (n > (unsigned)MIN_INT / 10 || (n == (unsigned)MIN_INT / 10 && c > (unsigned)MIN_INT % 10)))
{
n = MIN_INT;
break;
}
从而，字符串转换成整数，完整的参考代码为：

int StrToInt(const char* str)
{
static const int MAX_INT = (int)((unsigned)~0 >> 1);
static const int MIN_INT = -(int)((unsigned)~0 >> 1) - 1;
unsigned int n = 0;

//判断是否输入为空
if (str == 0)
{
return 0;
}

//处理空格
while (isspace(*str))
++str;

//处理正负
int sign = 1;
if (*str == '+' || *str == '-')
{
if (*str == '-')
sign = -1;
++str;
}

//确定是数字后才执行循环
while (isdigit(*str))
{
//处理溢出
int c = *str - '0';
if (sign > 0 && (n > MAX_INT / 10 || (n == MAX_INT / 10 && c > MAX_INT % 10)))
{
n = MAX_INT;
break;
}
else if (sign < 0 && (n >(unsigned)MIN_INT / 10 || (n == (unsigned)MIN_INT / 10 && c > (unsigned)MIN_INT % 10)))
{
n = MIN_INT;
break;
}

//把之前得到的数字乘以10，再加上当前字符表示的数字。
n = n * 10 + c;
++str;
}
return sign > 0 ? n : -n;
}
举一反三

实现string到double的转换
分析：此题虽然类似于atoi函数，但毕竟double为64位，而且支持小数，因而边界条件更加严格，写代码时需要更加注意。