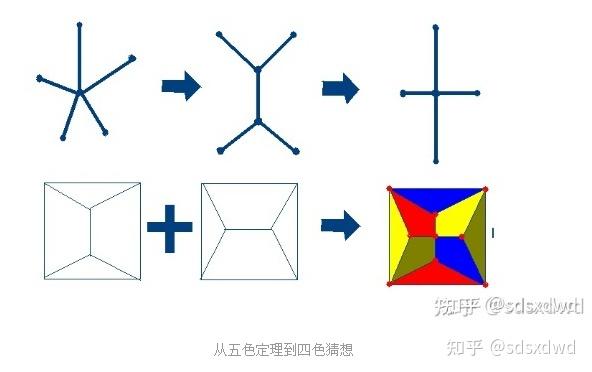
“四色问题”的平面着色游走“最短路径”解析

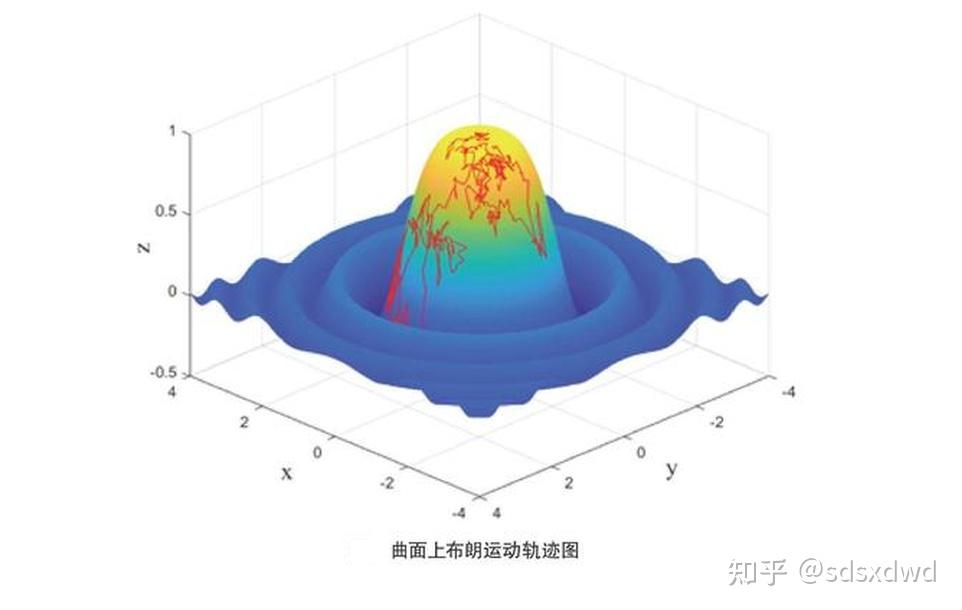
归一区间颜色的平面量子波,平均值为u,标准差为σ时,正态分布函数如下:
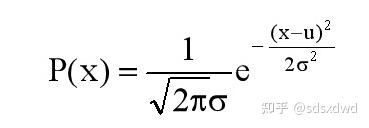
四色猜想 u=4 , \sigma=1 ,
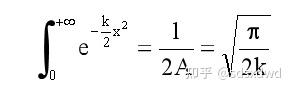
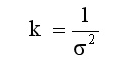
——欧拉恒等式 e^(iπ)+1=0 的证明 - 知乎
正态分布推导过程 - 知乎
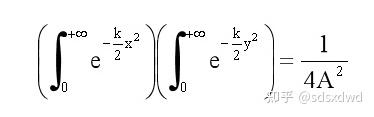
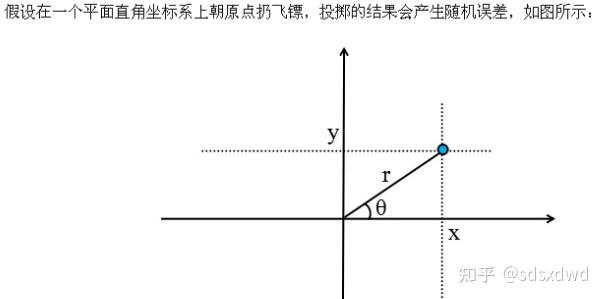
长期的论证表明,四种颜色够用(有特例),三种颜色是不够用的(有特例),五种颜色肯定够用(有逻辑证明),还证明,

二维平面内无法构造五个或五个以上两两相邻区域。
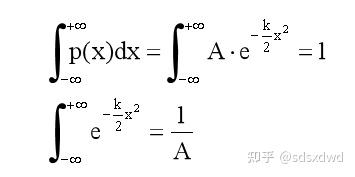
用数学语言来说就是,将平面任意地细分为不相重叠的区域,一张地图只需四种颜色来标记就行。
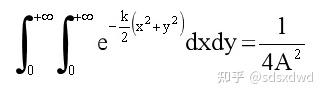
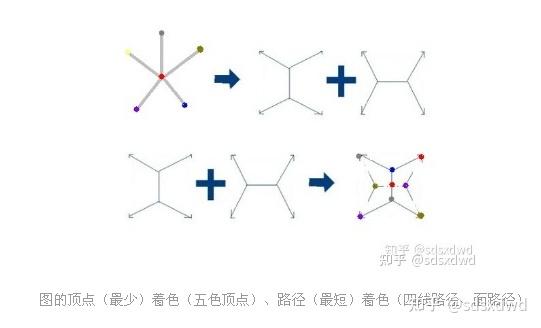
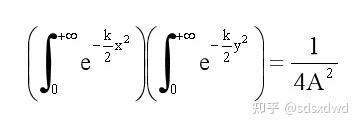
1.定义: 四色猜想,一面积图周围有 n 面积小图,
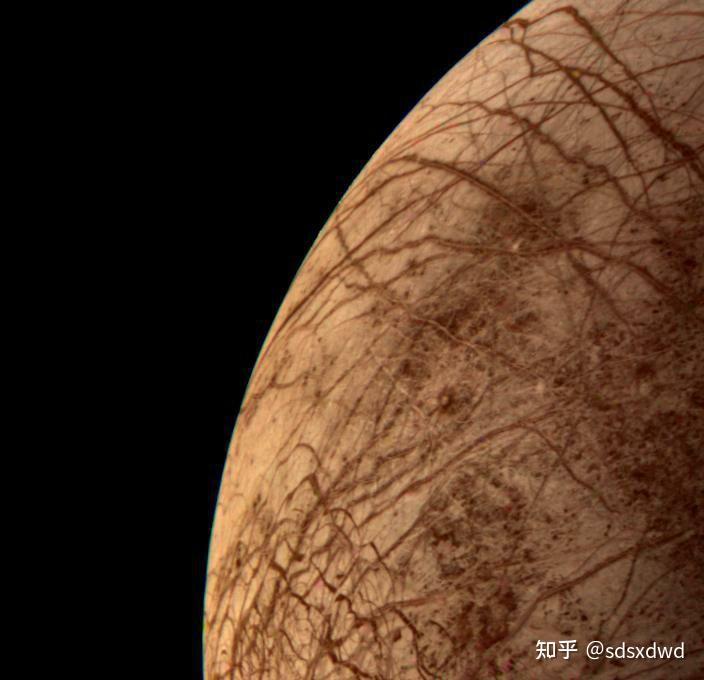
它们的颜色区分,颜色不重,
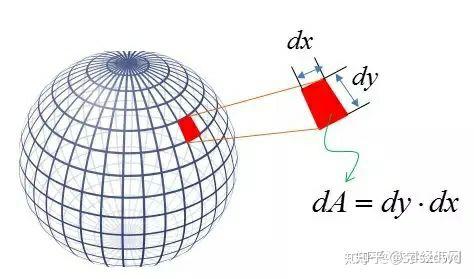
显然,四色猜想,面积填色的最短路径;

颜色对于地图区域的概率分布,当平均值为0,标准差为1时,标准正态分布函数如下:
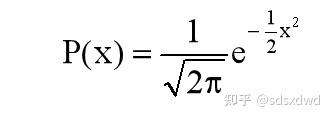
(色)散度,(图)旋度的垂直填充(堆积)
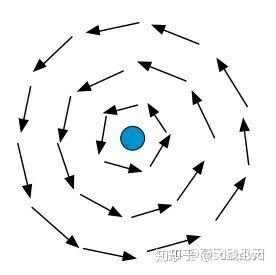
——填色,图的“散度”行为;定理证明,图的“旋度”行为 ——
2.最大面积最小周长区分最少颜色,面积图最小周长的最大面积,
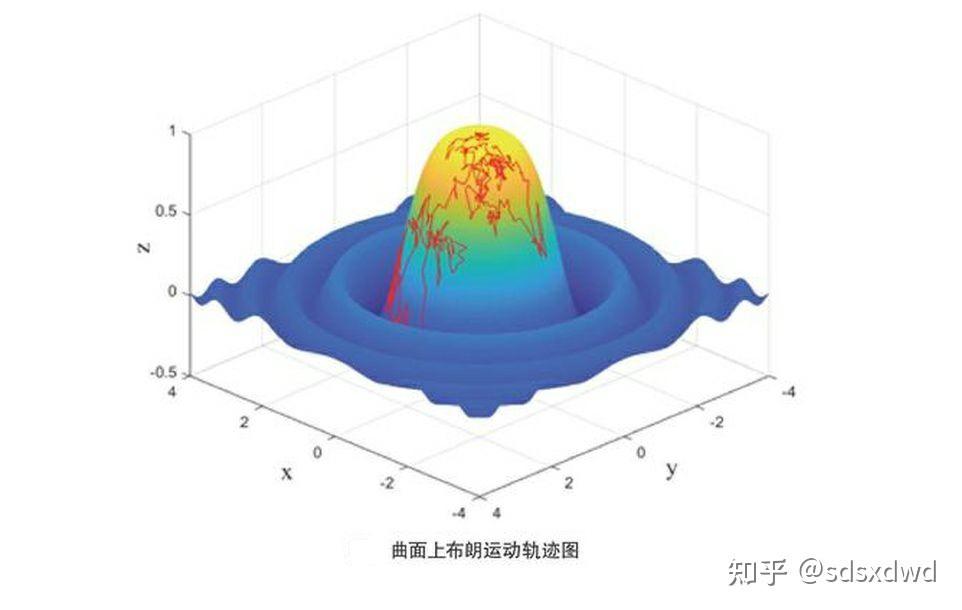
周径(面积图周长上的单样颜色 径弦平均 长)比等于颜色数;
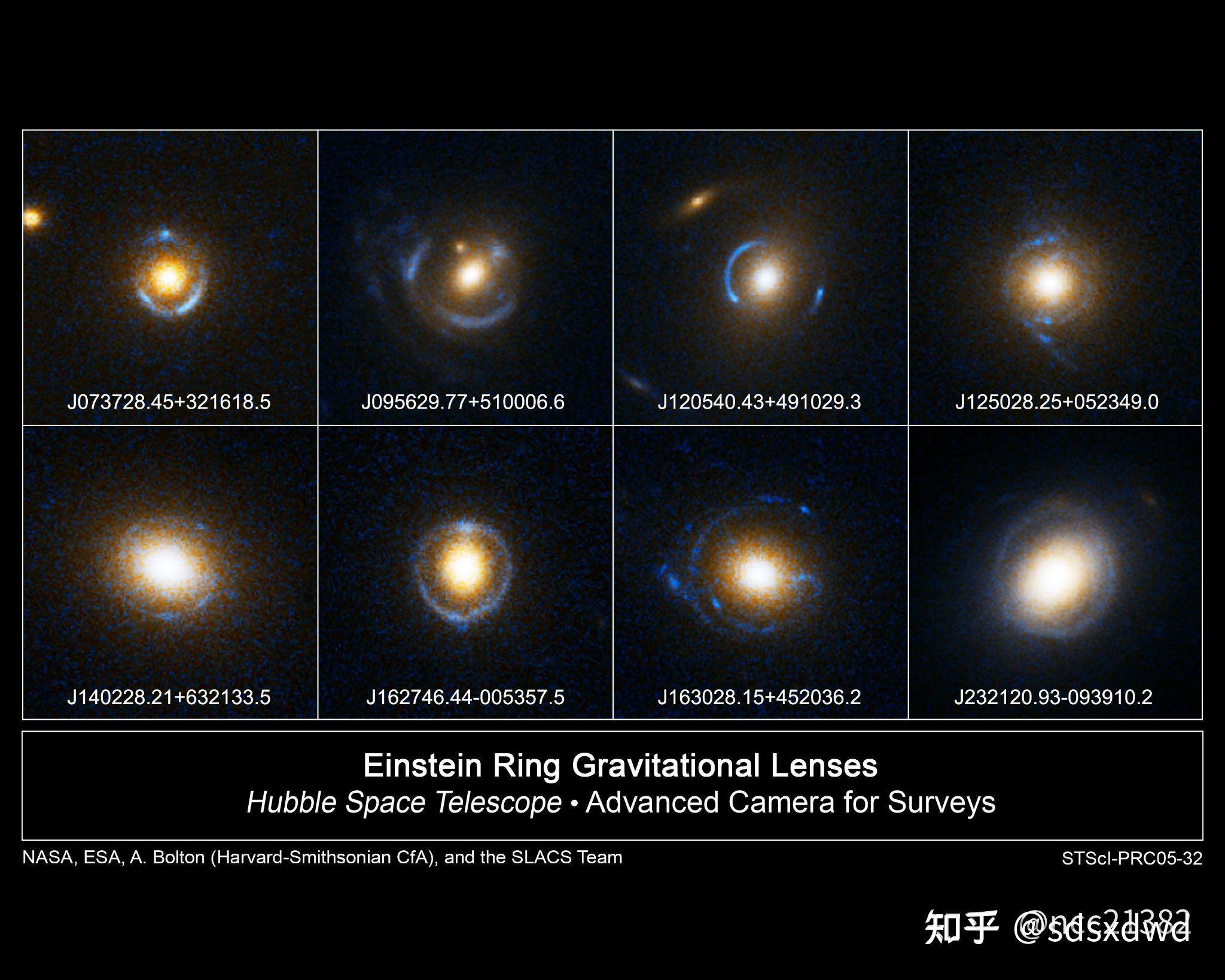
3.周长比任意短径,颜色数大于最少,周长比最大径长,最少颜色;
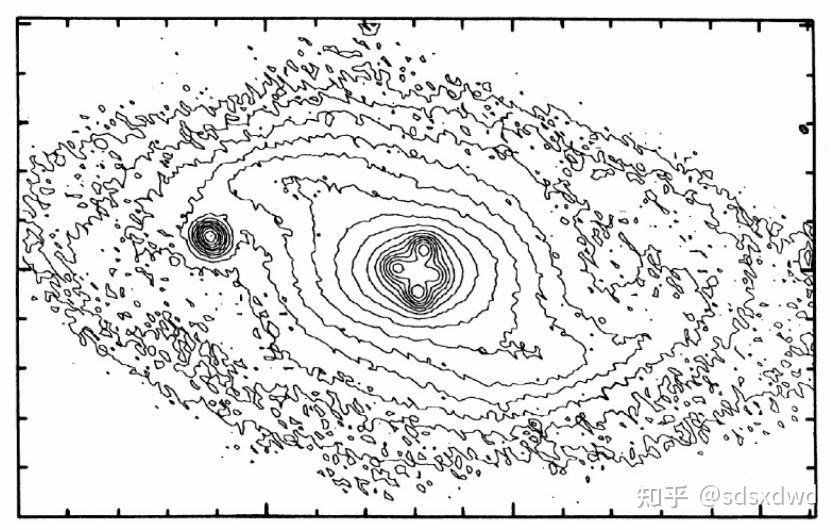
——如何看出平均曲率可以写成散度形式? - 知乎

4.于是有:圆周长比直径最小,最少颜色;周长比直径等于 \pi , \left[ \pi\right]\simeq4 ;
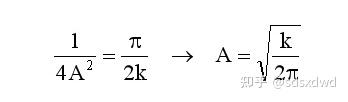
中心面积图(径长 \phi=\sum_{0}^{n}{T^{i}(\pi ^{i})} , T^{i} ,短径长, i=n )拓扑为点圆, G 4\sim 着色成立 .

当圆周外围被不等于0的小线段分割, \pi=4 .

5.对于非最大面积最小周长区分最少颜色,假设正方形为面积单元,有最短路径——
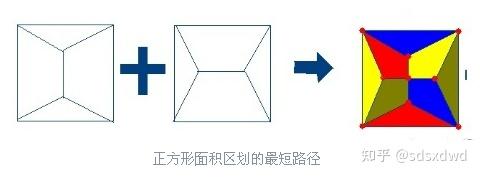

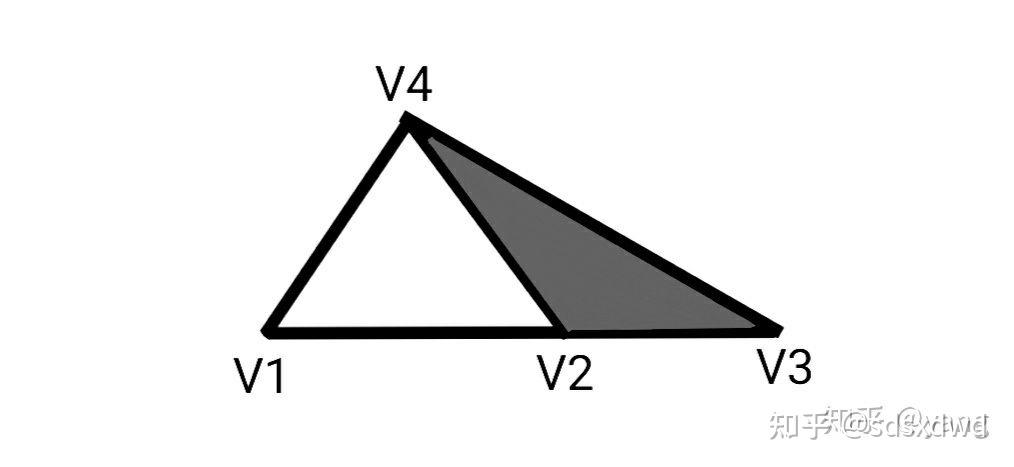
(1)对于二维平面的最基本图形是三角形 任何图形都可分为内部三角形的形式,三个相邻的三角形构成大三角形,三个图形有一个角相邻形成封闭
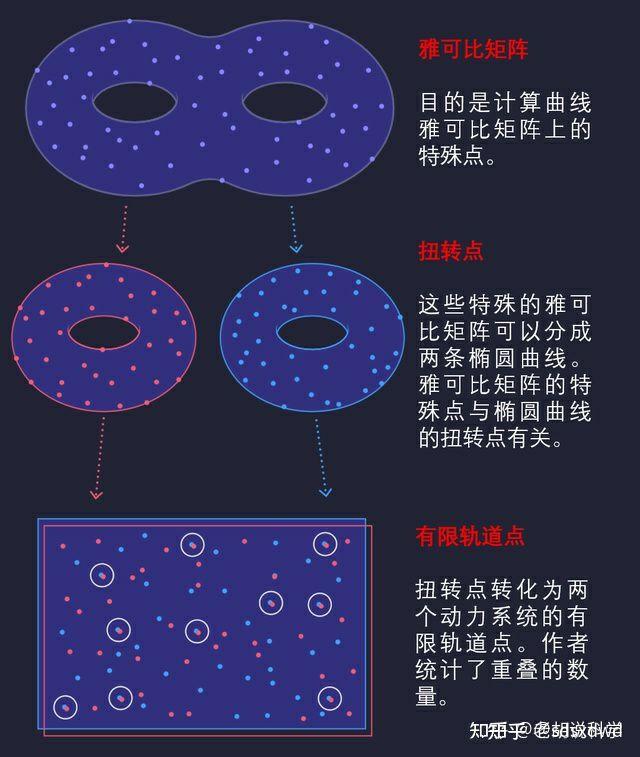
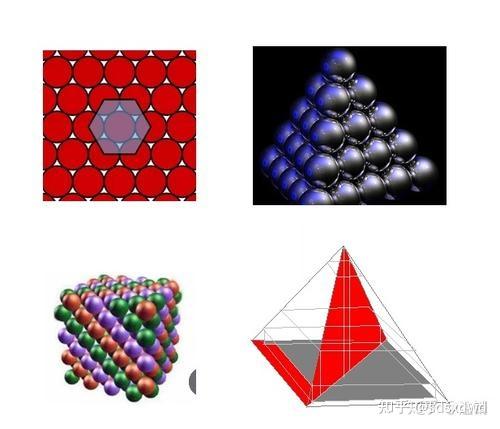
(前面说了任何图形都能转化为三角形,三角形是几何图的最密堆积,
所以这个大三角就是一个三角形,中间有一个点连着三个角)——
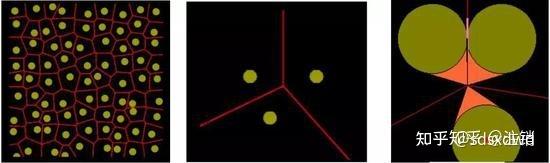
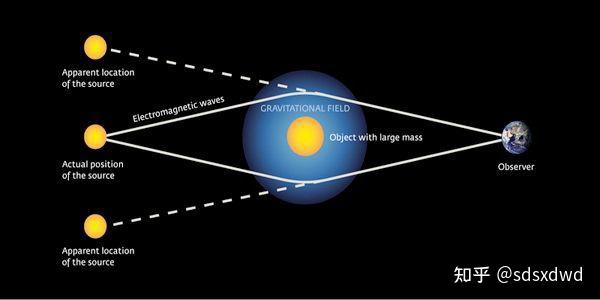
(2)这样的两个面积路径图形组合一起——长方形、四边形面积图区划最短路径:

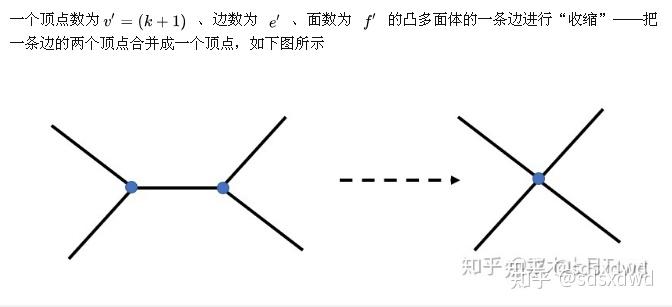
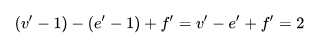
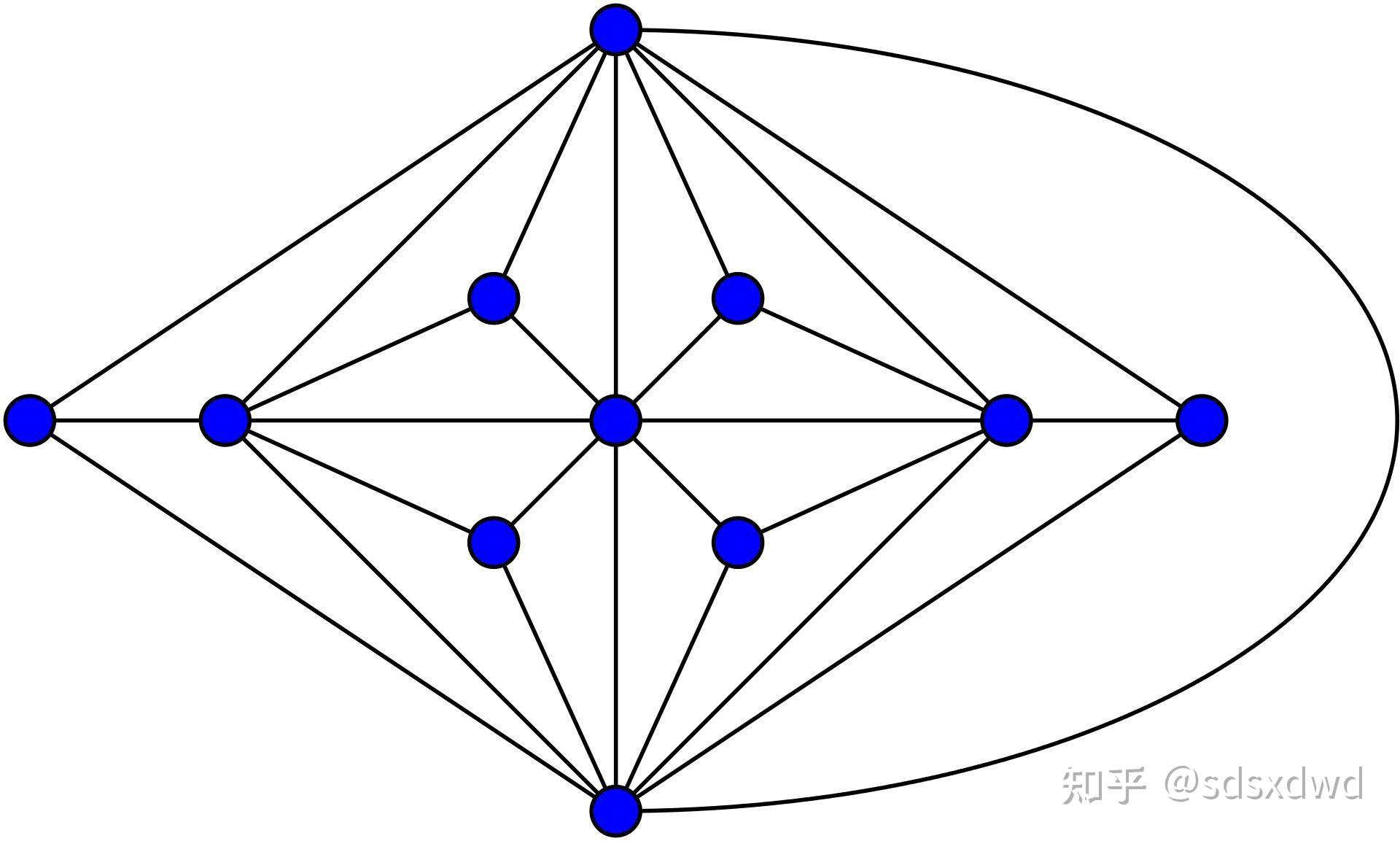
(3)于是有着色等价变换——从五色定理到四色猜想: