【度量和评分】sklearn 量化预测质量评估

BPCM

正在发芽的豆苗

sklearn有三种不同的API用于评估模型预测的质量：

估计器评分方法： 估计器有一种评分方法，为他们设计要解决的问题提供默认的评估标准。这一点在本次没有讨论，可以通过浏览每个估价器的文档进行学习。

评分参数： 使用交叉验证等模型评估工具（如model_selection.cross_val_score和model_slection.GridSearchCV）的内部评分策略。通过scoring参数设置指定评估工具。

度量函数： sklearn.metrics模块实现用于特定目的的预测误差评估功能。这些度量在分类度量、多标签排名度量、回归度量和聚类度量部分中有详细说明。

最后，虚拟估值器有助于获得随机预测的这些指标的基线值。

3.3.1.评分参数：定义模型评价规则

使用model_selection等工具进行模型选择和评估。model_selection.GridSearchCV 和 model_selection. cross_val_score中使用一个scoring参数来控制它们应用于评估的估计器的度量。

class sklearn.model_selection.GridSearchCV(estimator, param_grid, *, scoring=None, 
n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score=nan, 
return_train_score=False)
sklearn.model_selection.cross_val_score(estimator, X, y=None, *, groups=None, scoring=None, 
cv=None, n_jobs=None, verbose=0, fit_params=None, pre_dispatch='2*n_jobs', error_score=nan）

3.3.1.1.常见案例：预定义值

对于最常见的用例，您可以使用scoring参数指定一个评分器对象；下表显示了所有可能的值。所有评估器对象都 遵循较高返回值优于较低返回值的约定 。因此，度量模型与数据之间距离的度量，例如：metrics.mean_squared_error，可以用neg_mean_squared_error返回度量的负值，以满足上面的基本约定。

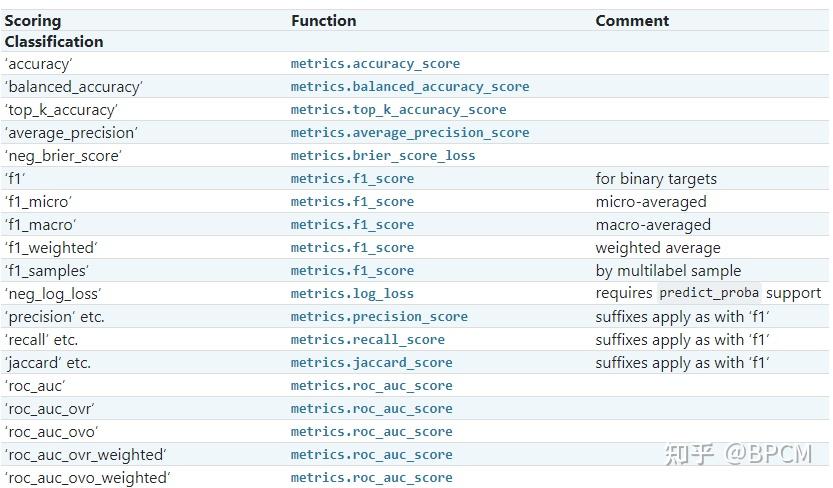
案例：

from sklearn import svm, datasets
from sklearn.model_selection import cross_val_score
X, y = datasets.load_iris(return_X_y=True)
clf = svm.SVC(random_state=0)
cross_val_score(clf, X, y, cv=5, scoring='recall_macro')
# array([0.96666667, 0.96666667, 0.96666667, 0.93333333, 1.        ])

3.3.1.2. 根据度量函数定义评分策略

sklearn.metrics模块还公开了一组简单的函数，用于测量给定原始数据和预测的预测误差：

以_score结尾的函数返回一个要最大化的值，越高越好。
以_error或_loss结尾的函数返回一个要最小化的值，越低越好。使用make_scorer转换为scorer对象时，请将greater_is_better参数设置为False（默认为True；请参阅下面的参数描述）。

以下各节详细介绍了各种机器学习任务的可用指标。

许多指标没有指定名称用作评分值，有时因为它们需要额外的参数，例如fbeta_score。在这种情况下，您需要生成适当的评分对象。生成可调用对象进行评分的最简单方法是使用make_scorer。该函数将度量转换为可用于模型评估的可调用项。

一个典型的用例是将库中的现有度量函数包装为其参数的非默认值，例如fbeta_score函数的beta参数：

from sklearn.metrics import fbeta_score, make_scorer
from sklearn.model_selection import GridSearchCV
from sklearn.svm import LinearSVC
# 将度量转换为可用于模型评估的可调用项
ftwo_scorer = make_scorer(fbeta_score, beta=2)
grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
                   scoring=ftwo_scorer, cv=5)

第二个用例是使用make_scorer从一个简单的python函数构建一个完全自定义的scorer对象，它可以接受几个参数：

您想要使用的python函数（在下面的示例中为my_custom_loss_func）
python函式是返回一个分数（greater_is_better=True，默认值）还是一个损失（greater _is_better=False）。如果是loss，python函数的输出将被scorer对象取负值，这符合scorers为更好的模型返回更高值的交叉验证约定。
仅用于分类度量：您提供的python函数是否需要连续的决策确定性（needs_threshold=True）。默认值为False。
任何其他参数，例如f1score中的beta或labels。

以下是构建自定义记分器和使用greater_is_better参数的示例：

import numpy as np
from sklearn.dummy import DummyClassifier
def my_custom_loss_func(y_true, y_pred):
    diff = np.abs(y_true - y_pred).max()
    return np.log1p(diff)
score = make_scorer(my_custom_loss_func, greater_is_better=False)
X = [[1], [1]]
y = [0, 1]
clf = DummyClassifier(strategy='most_frequent', random_state=0)
clf = clf.fit(X, y)
my_custom_loss_func(y, clf.predict(X))
# 输出：0.6931471805599453
score(clf, X, y)
# 输出：-0.6931471805599453

3.3.1.3.自定义自己的评分对象

您可以通过从头构建您自己的计分对象，而无需使用make_scorer工厂来生成更灵活的模型评分器。对于可调用的记分器，它需要满足以下两个规则指定的协议：

可以使用参数（estimator，X，y）调用它，其中estimator是应该评估的模型，X是验证数据，y是X的标签（在受监督的情况下）或None（在无监督的情况中）；
它返回一个浮点数，用于量化X上的估计器预测质量（参考y）。同样，按照惯例，数字越大越好，因此如果您的记分器返回损失，则该值应为负值。

3.3.1.4.使用多指标评估

Scikit learn还允许在GridSearchCV、RandomizedSearchCVs和cross_validate中使用多种评估指标。

有三种方法可以为scoring参数指定多个评分指标：

字符串度量指标构成的列表：

scoring = ['accuracy', 'precision']

score名称和score函数构成的字典

from sklearn.metrics import accuracy_score
from sklearn.metrics import make_scorer
scoring = {'accuracy': make_scorer(accuracy_score),
          'prec':'precision'}

注意，dict值可以是scorer函数或预定义的度量字符串之一。

作为返回分数字典的可调用函数：

from sklearn.model_selection import cross_validate
from sklearn import datasets
from sklearn.metrics import confusion_matrix
from sklearn.svm import LinearSVC
X, y = datasets.make_classification(n_classes=2, random_state=0)
svm = LinearSVC(random_state=0)
def confusion_matrix_scorer(clf, X, y):
    y_pre = clf.predict(X)
    cm = confusion_matrix(y, y_pre)
    return {'tn': cm[0, 0], 'fp': cm[0, 1],
            'fn': cm[1, 0], 'tp': cm[1, 1]
cv_result = cross_validate(svm, X, y, cv=5, scoring=confusion_matrix_scorer)
print(cv_result)
{'fit_time': array([0.0045774 , 0.00227857, 0.00192642, 0.00206995, 0.00172496]),
 'score_time': array([0.00096321, 0.00078726, 0.0006187 , 0.00059295, 0.00057411]),
 'test_tn': array([ 5,  9,  8,  6, 10]),
 'test_fp': array([5, 1, 2, 4, 0]),
 'test_fn': array([0, 1, 2, 3, 2]),
 'test_tp': array([10,  9,  8,  7,  8])}

3.3.2.分类指标

sklearn.metrics模块实现了几个损失、得分和效用函数来衡量分类性能。某些度量可能需要正类的概率估计、置信值或二进制决策值进行概率估计。大多数实现都允许每个样本通过sample_weight参数提供对总分的加权贡献。

在下面的小节中，我们将描述这些函数中的每一个，前面是一些关于通用API和度量定义的注释。

3.3.2.1.从二分类到多类和多标签

一些度量基本上是为二分类任务定义的（例如f1_score、roc_auc_score）。在这些情况下，默认情况下，只计算正值标签，假设正值类的标签为1（尽管可以通过pos_label参数进行配置）。

在将二分类度量扩展到多类或多标签问题时，数据被视为二分类问题的集合，每个类一个。然后有多种方法可以跨类集合平均二进制度量计算，每种方法在某些情况下都可能有用。如果可用，应使用average参数从中选择。

“macro”只计算二分类度量的平均值，为每个类赋予相等的权重。在不经常出现的类仍然很重要的问题中，宏观平均可能是突出其性能的一种方法。另一方面，认为所有类都同等重要的假设往往是不正确的，因此宏平均会过分强调不常见类的通常低性能。
“weighted”通过计算二分类度量的平均值来解释类不平衡，其中每个类的分数根据其在真实数据样本中的存在进行加权。
“micro”使每个样本类对对总体指标的贡献相等（样本权重的结果除外）。这不是对每个类的指标求和，而是对组成每个类指标的股息和除数求和，以计算总商。在多标签设置中，可能首选微平均，包括忽略大多数类别的多类别分类。
“samples”仅适用于多标签问题。它不计算每类度量，而是计算评估数据中每个样本的真实类和预测类的度量，并返回它们的（sample_weight-weighted）平均值。
选择average=None将返回一个数组，其中包含每个类的分数。
虽然像二分类目标一样，多类数据作为类标签数组提供给度量，但多标签数据被指定为指示符矩阵，在该矩阵中，如果样本i具有标签j，单元格[i，j]的值为1，否则为0。

3.3.2.2.准确度得分（Accuracy score）

accuracy_score函数计算准确度，即正确预测的分数（默认值）或计数（normalize=False）。

在多标签分类中，函数返回子集精度。如果样本的整个预测标签集与真实标签集严格匹配，则子集精度为1.0；否则为0.0。

如果 \tilde{y} 是第 i 样本的预测值，并且 y_{i} 是相应的真值，则 n_{samples} 正确预测的分数定义为:

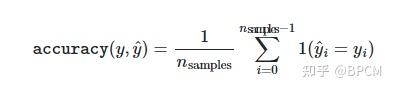
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)  # 输出： 0.5
accuracy_score(y_true, y_pred, normalize=False)  # 输出：2

3.3.2.3.Top-k准确度得分

top_k_accuracy_score函数是accuracy_score的泛化。区别在于，只要真实标签与k个最高预测分数中的一个相关联，预测就被认为是正确的。accuracy_score是k=1的特例。

该函数涵盖二分类和多类分类情况，但不包括多标签情况。

如果 \bar{f}_{i, j} 是对应于第 i 个最大预测分数的第 j 个样本的预测等级，并且是对应的真值，则正确预测的分数超过 n_{samples} 的部分定义为:

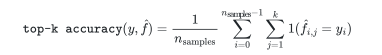
其中 k 是允许的猜测次数， 1(x) 是指示符函数。

import numpy as np
from sklearn.metrics import top_k_accuracy_score
y_true = np.array([0, 1, 2, 2])
y_score = np.array([[0.5, 0.2, 0.2], 
                    [0.3, 0.4, 0.2], 
                    [0.2, 0.4, 0.3], 
                    [0.7, 0.2, 0.1]])
top_k_accuracy_score(y_true, y_score, k=2)  # 0.75
top_k_accuracy_score(y_true, y_score, k=2, normalize=False) # 3

3.3.2.4.平衡精度分数（Balanced_accuracy_score）

Balanced_accuracy_score函数计算平衡精度，避免对不平衡数据集进行夸大的性能估计。它是每个类别的召回分数的宏观平均值，或者相当于原始准确度，其中每个样本根据其真实类别的反向流行率进行加权。

因此，对于平衡数据集，分数等于准确度。

在二元情况下，平衡准确度等于灵敏度（真阳性率）和特异性（真阴性率）的算术平均值，或具有二元预测而非分数的ROC曲线下的面积：

如果分类器在任何一类上都表现得同样好，则该术语会降低到常规精度（即，正确预测数除以预测总数）。

3.3.2.5. 分类报告（Classification report）

classification_report函数构建一个显示主要分类指标的文本报告。下面是一个自定义target_names和推断标签的小例子:

from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 1, 0]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
# 输出：
               precision    recall  f1-score   support
     class 0       0.67      1.00      0.80         2
     class 1       0.00      0.00      0.00         1
     class 2       1.00      0.50      0.67         2
    accuracy                           0.60         5
   macro avg       0.56      0.50      0.49         5
weighted avg       0.67      0.60      0.59         5

3.3.2.9 精度、召回率和 f-measures（Precision, recall and F-measures）

在二元分类任务中，术语“正”和“负”指的是分类器的预测，术语“真”和“假”指的是该预测是否与外部判断(有时称为“观察”)相对应。

在一个数据集检测中，会产生四类检测结果：

TP、TN、FP、FN：

T --- true 表示正确

F --- false 表示错误

P --- positive 表示积极的，看成正例

N --- negative 表示消极的，看成负例。

在TP、TN、FP、FN中P/N分别代表预测结果的类型为正例或负例，那么：

TP --表示：预测是正例，并且预测正确了（ 真阳性 ）；

TN --表示：预测是负例，并且预测正确了（ 真阴性 ）；

FP --表示：预测是正例，但是预测错误了（ 假阳性 ）；

FN --表示：预测是负例，但是预测错误了（ 假阴性 ）；

TP+FP+TN+FN：表示样本总数；

TP+FN：表示正样本数；

TP+FP：表示预测结果是正样本的总数，包括预测正确的和预测错误的。

FP+TN：实际负样本总数；

TN+FN：预测结果为负样本的总数，包括预测正确的错误的。

（1）精确率（Precision）

表示预测为正样本中有多少是真正的正样本（找的对）。预测结果中真正的正例的比例。

用途：评估检测成功基础上的正确率

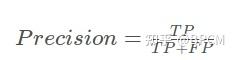
（2）召回率（Recall）

表示样本中正例有多少被预测正确了（找的全），所有正例被正确预测出来的比例。

用途：评估对所有检测目标的检测覆盖率

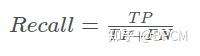
（3） F-measures

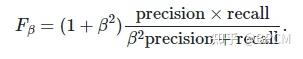
from sklearn import metrics
y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]
metrics.f1_score(y_true, y_pred)  # 0.6666666666666666
metrics.fbeta_score(y_true, y_pred, beta=1)  # 0.6666666666666666
metrics.fbeta_score(y_true, y_pred, beta=0.5)  # 0.8333333333333334

（4）多分类任务

在多类和多标签分类任务中，精度、召回率和f -度量的概念可以独立应用于每个标签。有几种跨标签组合结果的方法，由average_precision_score(仅多标签)、f1_score、fbeta_score、precision_recall_fscore_support、precision_score和recall_score函数的平均参数指定，如上所述。请注意，如果包括所有标签，“micro”平均在多类设置将产生精度，召回率和F所有相同的准确性。还要注意，“weighted” 平均可能产生一个F-score，不是在精度和回忆之间。

3.3.2.12. Log loss

对数损失，也称为逻辑回归损失或交叉熵损失，是在概率估计上定义的。它通常用于(多项)逻辑回归和神经网络，以及在期望最大化的一些变体中，并可用于评估分类器的概率输出(predict_proba)，而不是它的离散预测。

对于 y\in \left\{ 0, 1 \right\} 二分类任务:

from sklearn import metrics
y_true = [0, 1, 0, 1]
y_pred = [[.9, .1],[.8, .2], [.3, .7], [.01, .99]]