可用于大规模点云表面重建的深度学习算法

整理人：袁赣张秦，付前程，张琛，廖新耀

论文：

[1] Zhengxin Mi, Yiming Luo, Wenbing Tao*. SSRNet: Scalable 3D Surface Reconstruction Network. CVPR 2020.

[2] Yiming Luo, Zhengxin Mi, Wenbing Tao*. DeepDT: Learning Geometry From Delaunay Triangulation for Surface Reconstruction. AAAI 2021.

SSTNet 代码链接：

https:// github.com/wenbingtao/S SRNet

DeepDT 文章及代码链接：

https:// arxiv.org/abs/2101.1035 3

https:// github.com/wenbingtao/D eepDT

背景

从3D点云中重建易于表达和操作的三角网格表面，是三维建模及渲染、虚拟现实和增强现实等领域应用的重要基础，是计算机视觉和图形学中的重要研究问题。传统的几何重建方法一般可以分为两类：一种是基于隐式函数的表面重建，另一种是基于徳劳内三角化的表面重建。

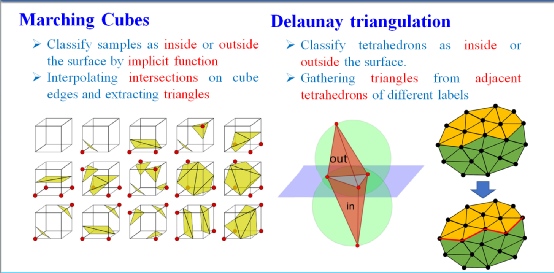
隐式函数的表面重建以Matching Cubes(MC)算法为基础（如图1左边），采用八叉树来表达点云数据。通常都是利用已知的点云数据估计一个潜在曲面的隐式表达函数，然后利用该函数对八叉树节点的顶点进行分类，分别标记为曲面的里面和外面，最后采用MC方法提取三角网格表面。这类方法又分为局部和全局的方法，局部方法有符号距离法（SDF）、截断符号距离法（TSDF）以及最小二乘法等，而全局方法最有代表性的是泊松表面重建方法，也是目前三维表面重建中使用最为广泛的方法之一。

基于徳劳内三角化的表面重建是基于空间点云的四面体表达（如图1右边）。首先将空间点云进行德劳内三角化，然后将空间四面体集合转化为一个图结构，每个四面体对应图的一个节点，相邻的节点用边连接起来，利用先验的可见性信息(visibility information)计算每个节点的数据项，进而采用Graph cuts算法对图节点进行二分类，二分类后的空间边界即为重建的三角网格表面。

问题

在最近两年，深度学习开始用于解决表面重建问题，并取得了一些进展，如Deep Marching Cubes(CVRP18)、ONet(CVPR19)、Deepsdf(CVPR19)等。这些方法基本的设想是基于点云数据学习一个类似隐式函数的分类器，对八叉树的顶点进行分类，然后采用MC方法提取表面。但是这些方法面临以下几个方面的问题：

1）处理的数据规模有限，大都仅能处理几千到几万的小规模点云数据，而且大多数情况下需要对原始点云数据进行降采样，进一步减少数据的规模，如ONet(CVPR19)会把原始点云降采样到800个点进行处理，否则由于太大的内存消耗算法很难有效工作。

2）对结构复杂细节丰富的点云数据表面重建效果不佳。这是由于算法采用的特征大都是借鉴点云语义识别的特征，而这类特征主要关注与语义相关的点云形状信息，而非点与其潜在曲面之间的空间位置关系，因而使得重建的表面细节表达能力不足。另一个原因是现有的表面重建网络处理大规模点云数据的能力不足，因而很多情况对原始点云进行了过多的降采样，如ONet会将原始点云降采样到800点进行处理，这就使得数据本身就丢失很多细节信息，自然导致细节重建能力较弱。

3）网络在训练时要求的样本量较大，如ONet在ShapeNet数据集上使用4/5的样本进行训练，并且训练得到的模型泛化能力较差，对没有充分训练的形状重建效果不佳。其主要原因也是由于采用的特征偏重于学习点云的形状结构，而非点和潜在曲面的关系，因而使得算法要求的训练样本较大，且对未经训练的形状模型泛化能力不足。

贡献

针对以上问题，来自华中科技大学的研究人员提出了可扩展的三维表面重建网络SSRNet和基于深度学习的徳劳内三角化表面重建网络DeepDT，分别在CVPR20和AAAI21上发表。算法不仅能够有效地恢复具有噪声和复杂拓扑结构的输入数据的几何细节，从而获得高完整性的三维模型，而且能够适用于大规模点云数据的表面重建。算法在公开的三维重建评测数据集ShapeNet、DTU和Stanford 3D数据集上进行测评获得优异的性能，效果不仅优于当前的基于深度学习表面重建算法，而且达到甚至超过了经典的德劳内三角化表面重建和泊松表面重建等方法。

这些工作的贡献可概括如下：

1）SSRNet采用局部区域点云的符号距离作为初始特征输入进行编码，网络重点学习的是点和潜在曲面的内外关系，而不关心点云的形状表达，这使得学习到的网络模型与点云数据的形状无关，因而具有很好的泛化性能，对未训练过的形状也能很好的重建。

这种与形状无关的特性也使网络只需要较少的样本训练就能达到好的性能，且网络参数较少。SSRNet所需要的训练数据只有ONet的1/10，模型大小为ONet的1/27，但是性能大大优于ONet方法，能够达到与经典的泊松表面重建方法相当的效果。而以往的基于深度学习的表面重建方法（如ONet、DMC等）都远不如经典的泊松表面重建方法，后面的实验结果也清楚的说明了这一点。

2）SSRNet是首个可以应用到实际大规模点云数据表面重建的深度学习重建方法，可对数百万甚至更大规模的点云数据进行分块并行重建。

之前的深度学习表面重建算法大都只能用于几千到几万规模点云数据的表面重建，甚至对这样规模的点云都需要进行降采样才能够处理（如ONet）。所以之前的深度学习表面重建算法基本上都只能在ShapeNet数据集进行评测（每个点云数据一般为几千到几万），而无法在DTU和Stanford数据集上进行评测（每个点云数据一般包含几十万到几百万个点）。

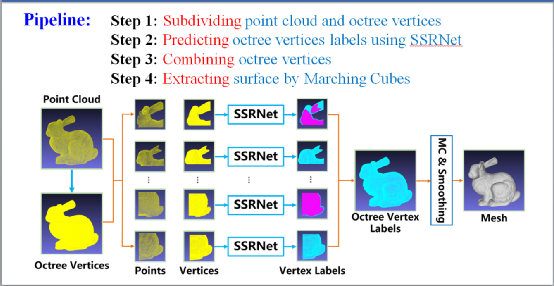
SSRNet采用的是局部特征，每个点的特征仅依赖于邻域点的符号距离，且网络的卷积操作也局限于局部，这使得SSRNet在表面重建时具有很好的扩展性。在处理大规模点云数据时，由于内存和显存的限制，数据不可能一次性装入内存和显存进行重建，而SSRNet的扩展性使得对大规模的点云数据，可以采用分块并行的方式完成重建（SSRNet重建流程如图2）。

3）首次将深度学习应用到徳劳内三角化表面重建中，提出了基于深度学习的徳劳内三角化表面重建算法DeepDT。

徳劳内三角化在划分空间时可以自适应的调整点云的采样密度，在点云越稠密的地方四面体越精细，因此能够平衡内存消耗与分辨率的关系。并且采用徳劳内三角化表面重建方法分块重建后的结果能够有效的进行拼接，因而在实际的大场景表面重建问题中被广泛应用。

使用徳劳内三角化进行表面重建的优点是显而易见的，但是传统的基于徳劳内三角化的方法需要利用可见性信息，无法处理任意点云。即使有可见性信息，其效果也并不理想。在实际的DTU数据的评测中，传统的徳劳内三角化表面重建算法效果均不如泊松表面重建算法（ShapeNet和Stanford数据由于缺乏可见性信息无法对徳劳内三角化表面重建算法进行评测）。其在实际大场景重建中能够广泛使用的主要原因是其具有可以接受的性能并且能够分块重建进行拼接。在小规模点云数据的重建中则很少使用德劳内三角化表面重建算法。

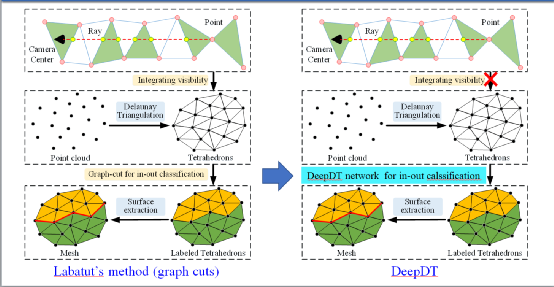
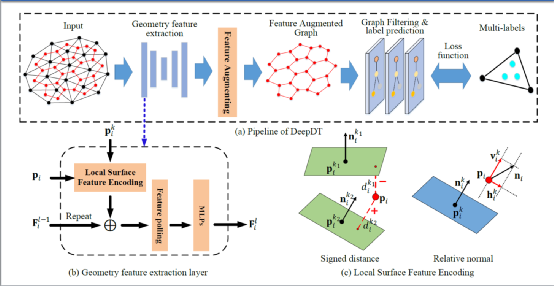
研究人员提出了基于深度学习的徳劳内三角化表面重建算法DeepDT（如图3所示）来解决以上问题。算法基于徳劳内三角化的优势，有着点云密度的自适应性以及高效率的特点。但相比传统的徳劳内表面重建方面而言，DeepDT并不需要可见性信息，能够处理任意点云，且重建效果良好，在ShapeNet、DTU和Stanford等数据上的评测效果达到甚至超过了泊松表面重建算法，大大优于传统的基于Graph cuts和德劳内三角化的表面重建算法。

SSRNet算法

SSRNet算法可以将输入的数据分块后分别重建，图2为算法的整体流程图。点云和构造出的对应八叉树的顶点被分块送入到SSRNet 网络里预测八叉树顶点的内、外，将所有的八叉树顶点分类后，使用MC算法与一个后平滑处理完成表面重建。

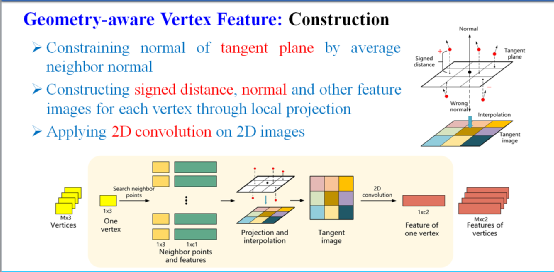
为了使网络增加对八叉树顶点分类准确度，又同时可以具有良好的泛化能力，点云及八叉树顶点的特征构造十分重要，研究人员提出利用点云和八叉树顶点周围的邻域点的特征来构造出一种具备几何感知能力的特征表达方法（如图4所示）。

SSRNet首先对点云中的每个点选取一个局部邻域，根据所有邻域点的法向计算一个主法向，以该点为中心做一个垂直于主法向的切平面，计算所有邻域点到该平面的符号距离，并通过插值将该邻域映射为一3*3的平面区域。由于特征已经映射成了二维平面特征，因而可以采用平面卷积进行编码处理。

在对点云的特征进行有效编码之后，同样为每个八叉树顶点构造一个切平面，这个切平面由八叉树顶点与其邻域点云确定。然后将邻域点云的特征投影到这个切平面上，计算有符号距离。此时这个切平面被认为蕴含了八叉树顶点分类所需要的局部几何信息，之后网络使用平面卷积进行进一步的特征处理，最后对八叉树的顶点进行分类。

使用图4的几何感知的顶点特征有如下好处：

1）直接学习度量点与面的空间关系的局部表面几何特征，更有利于准确判断点与曲面的相对位置关系，进而对顶点进行内/外分类。而过去的深度学习表面重建方法大都是借鉴点云语义识别方面的特征，因而更倾向于学习到点云的语义形状结构信息，反而不利于对顶点进行曲面的内/外分类；

2）由于特征具有局部性，在实际中每个点的特征构造只与邻域的点云相关，这使得输入点云数据具有可分性，容易扩展到处理大规模的点云数据；

3）切平面的构造可以预先并行计算，并且采用的2D卷积使得网络具有简洁高效的特点，相比其它深度学习表面重建算法，具有更高的效率，因而能够处理大规模数据。

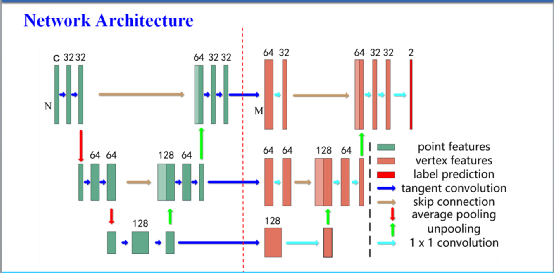
SSRNet 的网络结构如图5所示。它主要包含两个部分，左侧部分用于点特征提取，右侧用于顶点特征构建和顶点的标签预测，右侧顶点通过一个切平面卷积包含周围的点特征信息，完成特征的构建。网络的左侧部分编码输入点云的 个点的特征，它是具有跳跃连接的全卷积U形网络。网络的右侧部分是算法的核心，它首先用切平面卷积从对应尺度下的点云点特征中构造八叉树顶点的几何感知特征。然后使用1×1卷积和反池化操作编码更抽象的顶点特征，并预测每个顶点的标签。

DeepDT算法

经典的徳劳内三角化表面重建算法能够在划分空间时自适应调整点云的采样密度，在点云越稠密的地方四面体越精细，因此能够平衡储存计算量与分辨率的关系。且由于不俗的性能及高效易于拼接的特性因而在工程中广泛使用。

相比于传统的基于graph cuts的德劳内三角化表面重建方法，研究人员使用深度学习网络直接从点云及其徳劳内三角化中来预测徳劳内四面体的内外标签，不需要点云的可视性信息，避免了因可视性信息不足导致分类错误而产生的复杂多层表面的问题，能够应用于没有可视性信息的任意点云。传统的徳劳内表面重建方法与DeepDT的对比如图3所示。

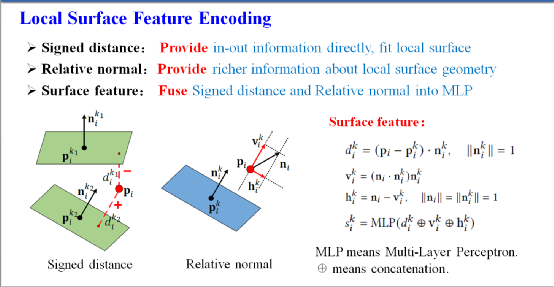
研究人员首先设计了几何特征提取模块，利用局部k近邻来为每个点编码局部几何特征。具体来说，对k近邻中每个点作一个垂直其法向的切平面，计算当前点到这k个平面的符号距离。在此基础上，将点云法向分解成邻域点切平面的相对法向作为输入，以提供表面更丰富的局部几何信息（如图6所示）。

在提取点的特征之后将其聚合到经徳劳内三角化后的图模型节点中，进而构造出一个特征增广图模型，图的节点与边分别对应着四面体以及相邻四面体之间的三角面。四面体的特征通过注意力机制从四面体四个顶点的特征中构造。

这样，通过聚集几何特征构建的图模型中的原始四面体特征就编码了四面体的内部/外部信息。基于经典图割的方法已经证明了图中的局部邻域平滑约束对于图节点的鲁棒标签预测是重要的。因此，在构建图特征之后，将多层图卷积网络应用到图中，以便集成更多的局部图结构约束（如图7所示）。

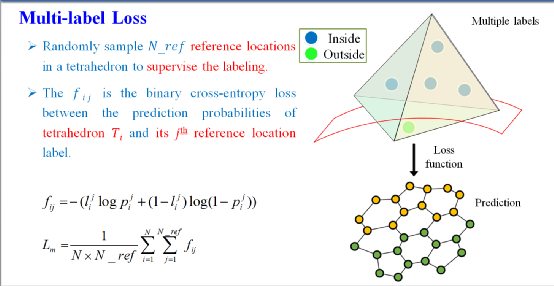
此外，研究人员在进行四面体的分类训练时，针对因四面体与表面之间的空间关系复杂、无法直接从ground truth表面生成四面体ground truth标签的问题，提出了一种多标签监督策略，能够在没有四面体ground truth标签或者可视性信息的情况下训练高质量的模型。在最后计算分类损失函数时设置了邻域一致性损失作为正则化损失，有助于建立更加平滑的表面（如图8所示）。

实验数据

研究人员在ShapeNet、DTU及Stanford 3D等三个数据集上对SSRNet和DeepDT算法进行评测。需要指出的是，过去的深度学习表面重建算法一般都只在ShapeNet上进行评测，而无法在规模比较大的DTU和Stanford 3D上进行评测。

ShapeNet上包含了45k个点云数据，均为封闭曲面，每个数据大约包含几千到几万个点云。DTU包含有106个点云数据，每个数据大约几百万个点云，大都为开曲面数据。Stanford 3D为比较早的点云数据集，仅包含3个点云数据。

SSRNet算法的实验结果

图9为SSRNet在ShapeNet上的实验结果，分别与几种最新的深度学习表面重建算法进行对比，也与经典的泊松表面重建算法(后面简称为PSR)进行了对比。从表中的结果可以看出，SSRNet算法的性能与PSR方法接近，大大优于其它的深度学习表面重建算法。特别与典型的ONet方法对比，SSRNet的训练样本只有ONet的1/10，模型参数为0.49M，而ONet的模型参数有13.4M。从显示的视觉效果来看，也可以看出，对于较为复杂的形状结果，ONet基本上重建失败，而SSRNet可以达到与PSR方法视觉效果相当的性能。

图10为SSRNet在DTU上的实验结果。DTU的数据大都为开曲面，目前的深度学习表面算法如ONet等只能重建闭曲面。泊松表面重建算法在重建开曲面的时候仍然会得到一个闭曲面，然后采用trimming方法进行处理得到相应的开曲面。SSRNet对开曲面和闭曲面均可以重建，针对闭曲面，SSRNet对八叉树顶点进行内/外分类，针对开曲面，则是对八叉树顶点进行前/后分类。SSRNet选取DTU的106个数据中的6个进行训练，模型的重建结果及与PSR的对比结果如图10所示。从视觉效果来看，SSRNet与PSR的结果没有差异，而从最终的评价指标来看，SSRNet在DTU上的结果甚至略优于PSR方法。主要原因是PSR方法在重建开曲面时仍然是生成一个封闭的曲面，然后进行裁剪得到开曲面，这会导致PSR结果出现轻微的扭曲，而SSRNet则是直接得到开曲面。因此，SSRNet方法在重建开曲面时具有比泊松表面重建更明显的优势。

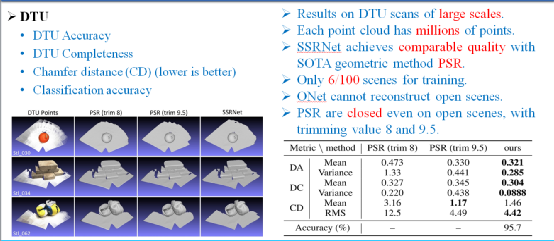
图11为SSRNet在Stanford 3D上的实验结果。Stanford 3D仅包含3个数据，如图11所示，因此无法在上面进行训练，这里采用SSRNet在ShapeNet和DTU上训练好的模型直接在Stanford数据上进行测试，两种模型得到的结果接近，均具有与PSR算法相当的效果。这也表明SSRNet方法良好的泛化性能。

DeepDT算法的实验结果

图12为DeepDT在ShapeNet上的实验结果，跟SSRNet一样，仍然采用其中4/50的数据进行训练，得到的模型参数为0.36M，甚至比SSRNet也略小，远小于ONet的13.4M。从结果来看，无论是视觉效果，还是评测数据，DeepDT都达到与PSR和SSRNet相当的性能。而传统的基于graph cuts和德劳内三角化的表面重建算法（后面简称为L-Method）由于ShapeNet数据集缺乏可见性信息，无法在这上面进行评测。

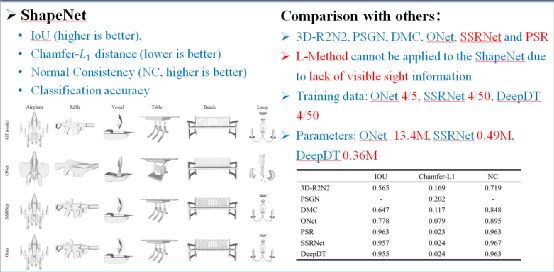
图13为DeepDT在DTU上的实验结果。DTU为实际扫描得到的数据，具有可见性信息，因而L-Method可以在上面进行评测。但是无论是从视觉效果，还是从实际的评测数据来看，L-Method的性能远不如DeepDT方法。DeepDT方法在上面仍然可以达到与PSR和SSRNet方法相当的性能。

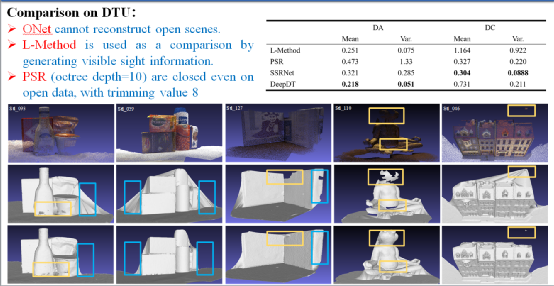
图13为DeepDT在Stanford数据集上的实验结果，Stanford没有足够的数据进行训练，因此采用ShapeNet上训练好的模型在上面进行测试。由于Stanford数据集缺乏可见性信息，L-Method无法在上面进行测试。这里仍然与ONet、PSR和SSRNet进行对比，从结果中可以看出，DeepDT在Stanford数据集上的效果仍然达到了PSR和SSRNet相当的性能。

结语

研究人员对经典的两大类型表面重建算法——基于隐式函数的表面重建和基于徳劳内三角化的表面重建——均采用深度学习方法进行了研究，提出了两种能够适用于实际的大规模点云数据表面重建的深度学习表面重建算法——SSRNet和DeepDT，效果超过了传统的L-Method方法，达到了经典的PSR算法的性能，未来有望在实际中广泛使用。

ACMH, ACMM, ACMP算法代码也已开源，欢迎大家下载测试：

[1] Qingshan Xu, Wenbing Tao*, Multi-Scale Geometric Consistency Guided Multi-View Stereo, In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 16-20，2019，Long Beach, CA, USA.

[2] Qingshan Xu, Wenbing Tao*, Planar Prior Assisted PatchMatch Multi-View Stereo, AAAI Conference on Artificial Intelligence (AAAI), Feb. 07-14, 2020, New York, USA.

https:// github.com/wenbingtao/A CMH

https:// github.com/wenbingtao/A CMM

https:// github.com/wenbingtao/A CMP

END