SPSSPRO只是娱乐娱乐，快速建模初步看看，发文章还得回归python呀。
直接丢出代码了哈：

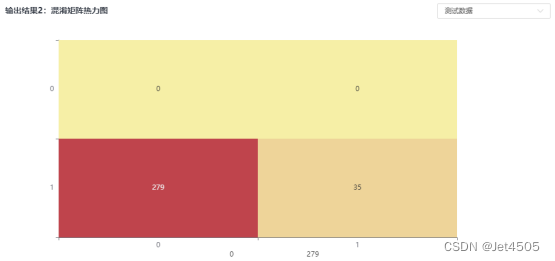
（A）混淆矩阵及其可视化：

y_pred = classifier.predict(X_test)
y_testprba = classifier.predict_proba(X_test)[:,1] 
y_trainpred = classifier.predict(X_train)
y_trainprba = classifier.predict_proba(X_train)[:,1]
from sklearn.metrics import confusion_matrix
cm_test = confusion_matrix(y_test, y_pred)
cm_train = confusion_matrix(y_train, y_trainpred)
print(cm_train)
print(cm_test)
#绘画测试集混淆矩阵
classes = list(set(y_test))
classes.sort()
plt.imshow(cm_test, cmap=plt.cm.Blues)
indices = range(len(cm_test))
plt.xticks(indices, classes)
plt.yticks(indices, classes)
plt.colorbar()
plt.xlabel('guess')
plt.ylabel('fact')
for first_index in range(len(cm_test)):
    for second_index in range(len(cm_test[first_index])):
        plt.text(first_index, second_index, cm_test[first_index][second_index])
plt.show()
#绘画训练集混淆矩阵
classes = list(set(y_train))
classes.sort()
plt.imshow(cm_train, cmap=plt.cm.Blues)
indices = range(len(cm_train))
plt.xticks(indices, classes)
plt.yticks(indices, classes)
plt.colorbar()
plt.xlabel('guess')
plt.ylabel('fact')
for first_index in range(len(cm_train)):
    for second_index in range(len(cm_train[first_index])):
        plt.text(first_index, second_index, cm_train[first_index][second_index])
plt.show()  
（B）灵敏度、特异度等数值型指标：
 
import math
from sklearn.metrics import confusion_matrix,roc_auc_score,auc,roc_curve
cm = confusion_matrix(y_test, y_pred)    
cm_train = confusion_matrix(y_train, y_trainpred)
#测试集的参数
a = cm[0,0]
b = cm[0,1]
c = cm[1,0]
d = cm[1,1]
acc = (a+d)/(a+b+c+d)
error_rate = 1 - acc
sen = d/(d+c)
sep = a/(a+b)
precision = d/(b+d)
F1 = (2*precision*sen)/(precision+sen)
MCC = (d*a-b*c) / (math.sqrt((d+b)*(d+c)*(a+b)*(a+c)))
auc_test = roc_auc_score(y_test, y_testprba) 
#训练集的参数
a_train = cm_train[0,0]
b_train = cm_train[0,1]
c_train = cm_train[1,0]
d_train = cm_train[1,1]
acc_train = (a_train+d_train)/(a_train+b_train+c_train+d_train)
error_rate_train = 1 - acc_train
sen_train = d_train/(d_train+c_train)
sep_train = a_train/(a_train+b_train)
precision_train = d_train/(b_train+d_train)
F1_train = (2*precision_train*sen_train)/(precision_train+sen_train)
MCC_train = (d_train*a_train-b_train*c_train) / (math.sqrt((d_train+b_train)*(d_train+c_train)*(a_train+b_train)*(a_train+c_train)))
auc_train = roc_auc_score(y_train, y_trainprba) 
保姆级解读




    
 
 
1、还记得怎么通过混淆矩阵计算灵敏度、特异度等指标么？
 
 首先获得a、b、c、d，怎么搞呢？a是不是第一行第一列，对于python来说：就是第零行第零列（a = cm[0,0]），以此类推，读取b、c、d。
 然后根据a、b、c、d包打天下，例如：
 灵敏度是真实值是1中，模型预测也为1的正确比例：sen = d/(d+c)；
 特异度是真实值是0中，模型预测也为0的正确比例：sep = a/(a+b)；
 其他的计算方式就不演示了。
 
 
2、此外，AUC的计算不依赖于a、b、c、d，而是根据这个代码：
 auc_test = roc_auc_score(y_test, y_testprba)
 roc_auc_score的参数呢，包括两个：y_test是实际值，y_testprba是预测的概率（注意，是概率，而不是分类，要和y_pred做区别），来看看代码：
 
y_pred = classifier.predict(X_test)
y_testprba = classifier.predict_proba(X_test)[:,1] 
 
来，一个是predict，一个是predict_proba，输出的如图所示。
 
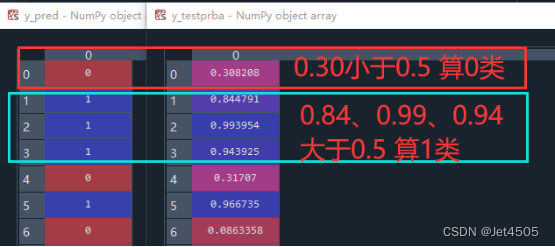
 一目了然了吧，就是根据0.5为阈值进行分类的。我们也可以根据这个表，找出被误判的样本，这个后面再说了。
 
 
3、对了，小白估计不知道这些参数去哪里看，还是多说一句吧：
 
 
 
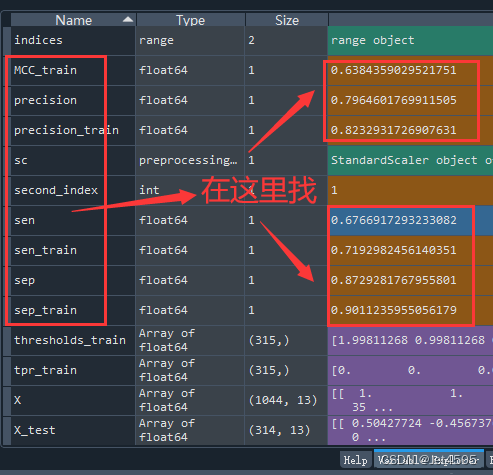
（C）ROC曲线：
 
#绘画训练集ROC曲线
fpr_train, tpr_train, thresholds_train = roc_curve(y_train, y_trainprba, pos_label=1, drop_intermediate=False)  
plt.plot([0, 1], [0, 1], '--', color='navy')     
plt.plot(fpr_train, tpr_train, 'k--',label='Mean ROC (area = {0:.4f})'.format(auc_train), lw=2,color='darkorange')
plt.xlim([-0.01, 1.01])  
plt.ylim([-0.01, 1.01])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate') 
plt.title('Please replace your title')
plt.legend(loc="lower right")
plt.show()
#绘画测试集ROC曲线
fpr_train, tpr_train, thresholds_train = roc_curve(y_test, y_testprba, pos_label=1, drop_intermediate=False) 
plt.plot([0, 1], [0, 1], '--', color='navy')     
plt.plot(fpr_train, tpr_train, 'k--',label='Mean ROC (area = {0:.4f})'.format(auc_test), lw=2,color='darkorange')
plt.xlim([-0.01, 1.01]) 
plt.ylim([-0.01, 1.01])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate') 
plt.title('Please replace your title')
plt.legend(loc="lower right")
plt.show()
保姆级解读
 
 
1、还记得ROC曲线的绘制原理么？传送门
 简单复习一下要点：指定一个阈值为90%，那么只有第一个样本（90%）会被归类为正例，而其他所有样本都会被归为负例，因此，对于90%这个阈值，我们可以计算出FPR为0，TPR为0.1（因为总共10个正样本，预测正确的个数为1），那么曲线上必有一个点为(0, 0.1)。依次选择不同的阈值（或称为“截断点”），画出全部的关键点以后，再连接关键点即可最终得到ROC曲线。
 所以要绘制ROC曲线，必须要获得三个数据：假阳性率（fpr），真阳性率（tpr）, 阈值（thresholds），python有一个代码直接给出结果：
 
fpr_train, tpr_train, thresholds_train = roc_curve(y_train, y_trainprba, pos_label=1, drop_intermediate=False)
 
也就是roc_curve函数，需要的参数有y_train（真实值）, y_trainprba（预测的概率，没错是概率，否则就是三个点的图），pos_label=1（告诉软件正类我们赋值为1），drop_intermediate=False就不用管他了。
 
 
2、我们来看一看具体输出了啥：
 
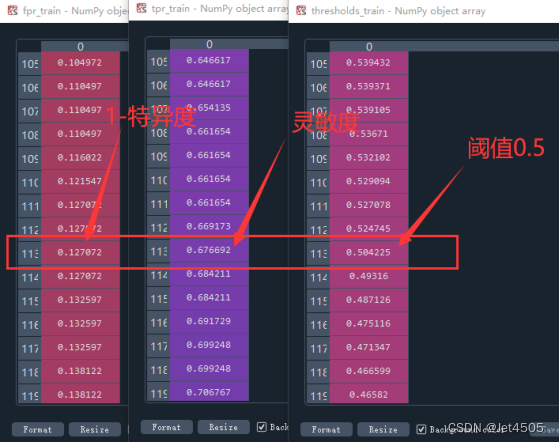
 来看看当阈值为0.5时，灵敏度是0.676692，特异度是1-0.127072=0.872928，是不是呢？我们找一下之前计算的结果（这里都是算测试集的哈）：
 
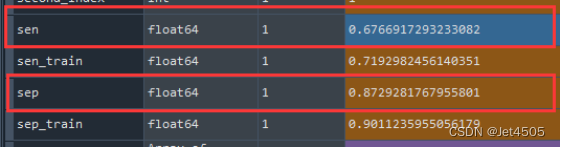
 没错吧，这都对应上了，进一步验证我们的代码和结果应该是没错的。
 
（D）PR曲线：
 上代码：
 
#绘画测试集PR曲线
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve, average_precision_score
precision_1, recall_1, thresholds = precision_recall_curve(y_test, y_testprba)
plt.step(recall_1, precision_1, color='darkorange', alpha=0.2,where='post')
plt.fill_between(recall_1, precision_1, step='post', alpha=0.2,color='darkorange')
plt.figure("P-R Curve")
plt.title('Precision/Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.plot(recall_1,precision_1)
plt.show()
AP_test = average_precision_score(y_test, y_testprba, average='macro', pos_label=1, sample_weight=None)
#绘画训练集PR曲线
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve, average_precision_score
precision_1, recall_1, thresholds = precision_recall_curve(y_train, y_trainprba)
plt.step(recall_1, precision_1, color='darkorange', alpha=0.2,where='post')
plt.fill_between(recall_1, precision_1, step='post', alpha=0.2,color='darkorange')
plt.figure("P-R Curve")
plt.title('Precision/Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.plot(recall_1,precision_1)
plt.show()
AP_train = average_precision_score(y_train, y_trainprba, average='macro', pos_label=1, sample_weight=None)
保姆级解读
 
 
为何要PR曲线？简单来说，对于不平衡数据，PR曲线是敏感的，随着正负样本比例的变化，PR会发生强烈的变化。而ROC曲线是不敏感的，其曲线能够基本保持不变。“在negative instances的数量远远大于positive instances的数据集里，PR更能有效衡量分类器的好坏。”
 具体区别和原理见此网站科普：
 https://blog.csdn.net/weixin_31866177/article/details/88776718
 统一在这里放出输出：
 
 
 
 
 
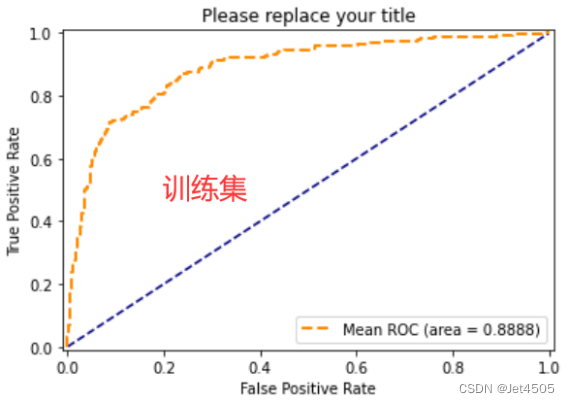
各位好好消化~
函数传入测试集，predict_proba的返回值是一个矩阵，矩阵的index是对应第几个样本，columns对应第几个标签，矩阵中的数字则是第iii个样本的标签为jjj的概率值。区别于predict直接返回标签值。
[1 1 2]
的意思是：第一组样本标签值为1、第二...
				
logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为"是"或"否"，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
同其他统计方法一样，二阶聚类也有严苛的适用条件，它要求模型中的变量独立，类别变量是多项式分布，连续变量须是正态分布。
步骤：1.预聚类，即对案例进行初步归类，也允许最大类别数由使用者决定；2.正式聚类，将步骤1的出局类别在进行聚类，并确定最终的聚类方案，并会根据一定的统计标准确定聚类的类别数量。
可以对变量或案例进行聚类，变量可以为
				
Logistic回归建模
       Logistic回归属于概率型非线性回归，对于二分类的Logistic回归，因变量y只有“是、否”两个取值，记为“是、否“两个取值，记为0和1。假设在自变量想，x1,x2.......,xp  作用下，y取“是”的概率是p，则取“否”的概率是1-p，研究的是当y取“是”发生的概率p与自变量x1,x2,x3……, xp
Logistic
				
评估指标是针对模型性能优劣的一个定量指标。一种评价指标只能反映模型一部分性能，如果选择的评价指标不合理，那么可能会得出错误的结论，故而应该针对具体的数据、模型选取不同的的评价指标。
针对不同类型的学习任务，我们有不同的评估指标，这里我们来介绍最常见的分类算法的一些评估指标。常用的分类任务评价指标有准确率（Accuracy）、精确率（Precision）、召回率（Recall）、Macro F1、Micro F1、P-R曲线（Precision-Recall Curve）、ROC、AUC、MCC、Cohen
				
本文首发于馆主君晓的博客，链接地址为：混淆矩阵及其相关评价指标
在机器学习或者深度学习领域，我们常常会用到混淆矩阵，以及与之相关的一些评价指标，今天就稍微总结一下什么是混淆矩阵以及里面的一些评价指标及其相关含义。
  混淆矩阵又叫做误差矩阵，是表示精度评价的一种标准格式，常常用n行n列的矩阵来表示，而通常在二分类的任务中，我们常常用下面的矩阵来表示混淆矩阵。
  上图是一个二分类混淆矩阵的标准形式，在二分类中0我们称之为负类，也就是negative，而1我们称之为正类，也就是positive
				
今天做数学建模2017B的时候用到了logistics分析来估计任务是否完成，给大家分享一下
二元logistics回归分析适用于因变量的结果只有两个的情况，例如任务的完成与否（0或1），通过对任务是否完成的影响因素可以估计出任务为完成或未完成的预测概率。
例如2017B中对任务是否完成的因素有任务所在地的用户密度和到城市中心的距离以及订单定价，我们通过SPPS二元逻辑分析来得出预测概率