Python数据分析实例-绕不过的假设检验(A/B测试)
在 上一篇文文章中 ,我们利用了模拟实验结合统计学常用分布函数泊松分布和正态分布解决了”奶茶店是否招人“的商业问题。除了利用模拟实验外我们还可以利用统计学中的 假设检验 回答商业问题。对假设检验不是很了解的同学可以参考 猴子的解释 。 本文涉及例子和数据纯属虚构,如有雷同纯属巧合。
本文会使用假设检验在商业中的应用 A/B测试 来回答问题:这次广告活动是否促进了购买?
我在一家主营欧洲市场的海外电商公司做数据分析师,在分析去年历史销售数据时发现在某一天的公司主营商品浏览量很高尤其是 英国市场 。在进行分析后发现当天是 英国的某一节日 ,所以我建议在 今年节日当天对英国市场的客户进行广告活动比如送消费券 ,以促进购买并提高客户转化率,从而利用节日当天流量大的优势提高销售额。
文章主要分为以下几个部分。
- 分析、理解问题
-
实验设计
2.1 确定实验组与对照组
2.2 确定分析指标
2.3 形成假设
2.4 确定需要收集的数据
2.5 流量分配设计
2.6 实验时间、与样本量
2.7 部署数据收集并确保实验功能和数据录入正常运行 - 实验分析
-
分析总结与建议
1. 分析、理解问题
主要目的:分析是否广告活动促进了英国市场节日当天的购买量。 回答这个问题显然不能简单地对比去年同期的购买量,因为不同时间的影响因素太多,即使投入广告活动导致了购买量增加,也可能是因为其他因素导致的购买量增加。
所以我们希望通过一个实验可以对比两个同时发生的组,一个组的用户可以看到广告活动,而另一个组看不到广告活动。这样就可以排除其他变量而只关注是否广告活动可以促进购买量。这个实验就是商业中广泛应用的A/B测试。
2. 实验设计
2.1 确定实验组与对照组
对比广告活动是否对购买行为有影响,我们只需要控制一个变量,所以只需把流量分成2组:
- 实验组(test group)-实验组参与广告活动
- 对照组(control group)-对照组用户无任何广告活动
2.2 确定分析指标
A/B测试指标一般分为以下几类:
- 各数或总和--比如总浏览人数,销售额等
- 均值、中位数或众数等--比如人均时长,平均页面载入时间等
- 比率类--如点击率,留存率,转化率等
广告活动的目的是为了让更多人购买产品,所以顾客看到广告后 是否促进了购买 是我们关心的。我们可以选择选择购买人数,或者转化率(购买率)作为指标。在本次实验中我选择了 转化率 (conversion rate,即购买人数/总人数)作为分析指标,因为实验中实验组和对照组的人数不一定同,用比率可以直观对比两组购买情况。
2.3 形成假设
A/B测试的基本思想是小概率反证法思想 。小概率思想是指小概率事件(P<0.01或P<0.05)在一次试验中基本上不会发生。反证法思想是先提出假设(零假设),再用适当的统计方法确定假设成立的可能性大小,如可能性小,则认为假设不成立,若可能性大,则还不能认为假设不成立。
接下来我们要针对问题提出假设,包括零假设( Null hypothesis ),和对立假设( Alternative hypothesis )。
- 零假设 :实验组与对照组的转化率没有差异(cr_t - cr_c = 0)
- 对立假设 :实验组与对照组的转化率有显著差异(cr_t - cr_c ≠ 0)
2.4 确定需要收集的数据
确定假设和指标后,我们需要决定实验要收集的数据。一般实验数据可以通过 数据埋点 、web服务器日志收集、网站分析工具(如Google Analytics)收集用户数据,针对此次实验的目的我们可以收集以下数据,同时我们也收集一些相关收据方便分析购买行为:
- 用户ID:用户登录名
- CookieID:当用户没有登录可以使用 CookieID 识别唯一用户
- 时间:进入页面时间
- 购买时间:用户下单时间
- 使用设备:使用何种设备登录网站
- 浏览器语言:浏览器使用的语言,比如英国的客户基本都使用英语,而西班牙的客户可能使用西班牙语。
- 使用浏览器类型:浏览器类型,比如Fox, Chrome等。
- 是否购买:用户购买标记为1,不够买则标记为0。这个数据是我们分析的重点。
- 分组:根据用户登录的信息按一定比例分为对照组A,实验组B。
- 其他数据等
我们需要排除同一用户的重复购买行为去除复购对实验的影响,所以只把唯一用户第一次浏览记录作为实验数据。此外为了简化,这里数据使用Python模拟数据,并只模拟 1)是否购买,2)分组数据 。数据表格每一行代表唯一用户第一次浏览记录。
2.5 流量分配设计
在实验中我们只需要对英国市场的顾客进行实验。此外,对于所有英国市场的顾客我们也需要决定哪些顾客是实验组,而哪些是对照组。对于流量分配的讨论 这个回答 写的不错,大家可以阅读下。
对于此次实验我们考虑经费有限,最终决定只对 10% 的英国市场的顾客进行广告活动。分流策略可以总结为以下图片。
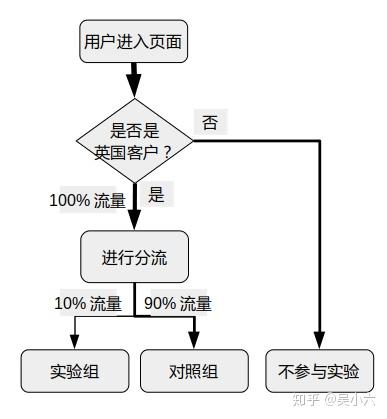
2.6 实验时间、与样本量
下一步要确定实验的样本量,因为实验是伴随着成本的,我们要用尽量小的成本去得到可靠的实验结果。如何计算需要的实验样本量,我们要了解一个知识点-功效分析( Power Analysis )。对于功效分析这里不再展开,我们只需要知道功效分析有4个指标,确定任意三个指标后就能推算第四个指标。这四个指标是:
效应值
简单来说就是一个衡量实验组和对照组均值差异的量度,效应值越大两组均值差异越大。我们可以通过最小改善程度(
Minimum Detectable Effect
)计算效应值。最小改善程度是指实验中希望看到的
相对于
指标参考值的最小提高值。比如一般转化率为5%,如果最小改善程度设置为1%,那实现期望观察到的转化率为5.05%。需要注意的是最小改善值指的是最小能够通过实验发现的提高,比如设置为1%,我们也能发现3%,10%甚至更高的提高。另外一个重要的点是,最小改善程度值设置越小,需要的实验数据也就越多。基于以上说明,
我们把最小改善程度设置为5%
,并使用Python包
statsmodels中proportion_effectsize
计算效应值。想要了解更多相关只是的同学可以看
这篇文章
。
统计学功效 是指当对立假设为真时正确地拒绝零假设的概率。统计学功效越高,出现 第二类错误 的概率越小。对于第二类错误不清楚的同学可以看下 知乎的问题讨论 。根据 这篇文章提到的论文 ,一般统计学功效设置为 80% 。
显著水平 可以解释对零假设的拒绝域,用α表示,一般选择0.01,0.05,0.10。对于显著水平和p值有疑惑的同学可以阅读下 知乎的这个问题讨论 。这里我们设定为 0.05 。需要注意的是我们的假设是 双尾检验 (因为我们不确定广告活动会提高还是降低转化率),所以计算得到p值后,p值需要小于0.025才能拒绝零假设。
对于第一类错误和第二类错误这里额外讨论下,因为理解这两类错误对于A/B测试是十分重要的。根据我们设置的显著水平和统计学功效,第一类错误和第二类错误的概率分别是5%(α)和20%(β)。第一类错误这里指错误地反驳了零假设,也就是说其实广告活动并不会带来大的转化率改变,而第一次错误使得我们接收零假设认为广告活动是有效的。 这有可能使公司花费人力财力,但其实是没有带来任何收益提升 。第二类错误是指错误地接受了零假设,即广告活动是有效的,但是我们认为他无效而没有投入广告。 这类错误并不会给公司带来额外损失 。因此,对第一类错误的控制需要更严格。
接下来我们利用Python三方包statsmodels中的来计算下需要的样本大小。
from statsmodels.stats.power import TTestIndPower
from statsmodels.stats.proportion import proportion_effectsize
effect = proportion_effectsize(.05, .0525) #平时转化率为5%,希望观察到的最小改善程度设置为5%,即5.25%。
alpha = .05 # .05双尾检验,每边为0.025
power = .80
ratio = 9 # 对照组是实验组流量的9倍。
# 计算实验组的样本量
test_size = TTestIndPower().solve_power(effect_size = effect,
power = power,
alpha = alpha,
ratio = ratio)
test_size = round(test_size)
control_size = test_size*9
print(f'对照组需要样本:{control_size},实验组需要样本:{test_size},总样本量:{test_size*10}')对照组需要样本:610533,实验组需要样本:67837,总样本量:678370
此外,根据去年节日流量的统计,当日此首推产品在英国市场的每小时平均流量达到了20万每小时。所以根据需要的样本总量除以小时流量,我们只需要 3.5小时 就可以收集到足够样本。
2.7 部署数据收集并确保实验功能和数据录入正常运行
实验设计的最后一步是部署数据收集并测试每个环节运行正常,以确保实验可以收集到正确的数据。比如:
- 在不同平台下(手机,电脑端等)是否正常工作
- 用户数据录入是否正常
- 数据分流是否正常
- 用户是否可以正确看到广告活动等。
3. 实验分析
收集到实验数据后,我们利用Python进行分析数据并确定是否拒绝零假设(认为广告活动会对顾客购买行为有较大影响)。
# 导入必要的包
from scipy.stats import bernoulli, ttest_ind, t
import numpy as np
import random
import pandas as pd
from math import sqrt模拟实验数据,因为本文主要目的是分享A/B测试的实现步骤,所以只使用了Python模拟数据。
def generate_data(n_t, n_c, cr_t = .0518, cr_c = .05, random_state = 123):
生成实验数据。
Params:
n_t(int):实验组数据数量。
n_c(int):对照组数据数量。
cr_t(float):实验组转化率(conversion rate)。
cr_c(float):对照组转化率。
Returns:
df(DataFrame): 生成的实验数据。
test = bernoulli.rvs(cr_t, size = n_t, random_state = 123)
df_test = pd.DataFrame({'group': ['test']*n_t,
'converted': test})
control = bernoulli.rvs(cr_c, size = n_c, random_state = 123)
df_control = pd.DataFrame({'group': ['control']*n_c,
'converted': control})
df = pd.concat([df_test, df_control])
df = df.sample(frac=1).reset_index(drop=True)
return df
# 每小时流量20万,测试3.5小时
t_size = int(200000 * 3.5 * 0.10)
c_size = int(200000 * 3.5 * 0.90)
df_data = generate_data(t_size, c_size)得到了实验数据df_data,先简单看下数据的基本信息。
# 查看数据前5行
df_data.head(5)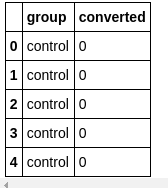
# 数据基本情况
df_data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 700000 entries, 0 to 699999
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 group 700000 non-null object
1 converted 700000 non-null int64
dtypes: int64(1), object(1)
memory usage: 10.7+ MB
数据每一行代表一个唯一顾客第一次的浏览数据,group说明了顾客是实验组(test group)还是对照组(control group),converted代表了顾客的购买情况(1表示购买,0表示没有购买)。
我们先看下实验组和对照组转化数量,转化率的对比。
# 统计转化数量和转化率
df_temp = df_data.pivot_table(values = 'converted', index = 'group', aggfunc = 'sum')
df_temp['total'] = df_data.pivot_table(values = 'converted', index = 'group', aggfunc = 'count')
df_temp['rate'] = df_temp['converted'] / df_temp['total']
cr_t = df_temp.loc['test', 'rate']
cr_c = df_temp.loc['control', 'rate']
print(f'实验组比对照组的转化率高{(cr_t - cr_c)/cr_c:.2%}')
df_temp实验组比对照组的转化率高4.11%
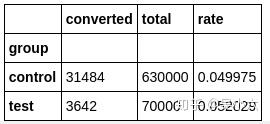
到这里你也许会有疑问,既然都算出来实验组的转化率比对照组的高,为什么不能说广告促进了购买呢?如果你有这个疑问,你需要明确收集到的数据是 样本 ,所以从样本计算出来的转化率并不一定代表总体的转化率。因此我们需要通过统计学的假设检验方法去计算p值并判断两个样本转化率 是否差异具有显著性 (p<0.025)。
接下来我们要选择一个检验类型。一般在对比两组差异时常用检验方法有t检验、z检验、卡方检验、方差分析等。对于本例数据是比较特殊的情况(是否转化可以理解为成功概率,每次顾客流量可以看成一次独立实验,因此符合 二项分布 ,并且实验次数大,可以近似看成正态分布),我们可以使用t检验,z检验或者卡方检验。
这里我选择使用t检验。
# 定义函数生成t检验报告
def t_report_two_tailed(data_t, data_c, h0, h1, alpha = .05):
进行双尾t检验并生成实验结果。
Params:
data_t(Series):实验组是否购买(转化)的Series。
data_c(Series):对照组是否购买(转化)的Series。
h0(str):零假设。
h1(str):对立假设。
alpha(float):显著水平数0.05。
Returns:
t_size = len(data_t)
c_size = len(data_c)
# 双尾t检验
t_value, p_value = ttest_ind(data_t, data_c)
# 自由度
degree_f = t_size + c_size -2
# 计算标准差
std_t = data_t.std()
std_c = data_c.std()
std_tc = sqrt(((t_size - 1)*(std_t)**2 + (c_size - 1)*(std_c)**2) / degree_f)
# 实验组和对照组转化率差值
diff_mean = data_t.mean() - data_c.mean()
# 计算误差范围,用于计算置信区间
margin_of_error = t.ppf(1-(alpha/2), degree_f) \
* std_tc * sqrt(1/t_size + 1/c_size)
ci_lower = diff_mean - margin_of_error
ci_upper = diff_mean + margin_of_error
print('A/B测试结果/n')
print('='*50)
print(f'零假设:{h0}')
print(f'对立假设:{h1}')
print('检验类型为:双尾检验')
print('显著水平为(alpha):0.05\n')
print(f'实验组样本数:{t_size},对照组样本数{c_size}')
print(f't检验结果为: \n\tt值 = {t_value:.5f}\n\tp值 = {p_value:.5f}')
print(f'\n实验组转化率为{data_t.mean():.5f},对照组转化率为{data_c.mean():.5f},两组差异为 {diff_mean:.5f}({diff_mean/data_c.mean():.2%})。')
print(f'两组差异的{1-alpha:1.0%}置信区间为[{ci_lower:.5f}({ci_lower/data_c.mean():.2%}) to {ci_upper:.5f}]({ci_upper/data_c.mean():.2%}))')
if p_value < (alpha/2):
print(f'p < {alpha/2}, 拒绝零假设,实验组与对照组有显著差异。')
else:
print(f'p > {alpha/2}, 不能拒绝零假设,不能说明实验组与对照组有显著差异。')
# 进行t检验
