如果需要计算Gamma函数,至少需要一台可以计算定积分的科学计算器。
根据Gamma函数的定义: \Gamma(s)=\int_{0}^{+\infty}\mathrm{e}^{-x}x^{s-1}\mathrm{d}x\ \ (s>0) ,这个积分因为涉及无穷上限,显然无法在科学计算器上直接计算,因此将积分变量 x 用 \mathrm{tan}\ x 进行换元,得到:
\Gamma(s)=\int_{0}^{\frac{\pi}{2}}\mathrm{e}^{-\mathrm{tan}\ x}(\mathrm{tan}\ x)^{s-1}(1+\mathrm{tan}^2x)\mathrm{d}x\ \ (s>0)
参考文章:
上式可以近似为:
\Gamma(s)=\int_{0}^{\frac{\pi}{2}-1\times10^{-10}}\mathrm{e}^{-\mathrm{tan}\ x}(\mathrm{tan}\ x)^{s-1}(1+\mathrm{tan}^2x)\mathrm{d}x\ \ (s>1)
把计算器的角度单位设为弧度,给 s 指定合适的值,输入上式即可进行计算。
这里以卡西欧的fx-991CN X为例进行计算:
\Gamma(1.3)\approx0.8974706963
\Gamma(2.5)\approx1.329340388
\Gamma(4.6)\approx13.38128587
\Gamma(6.7)\approx413.4075168
fx-991CN X计算出来的结果如下:

可以看到,这些结果在10位有效数字内都是精确的。
然而,限于科学计算器的计算范围,用上面的方法计算 0<s\leq1 的 \Gamma(s) ,科学计算器会报数学错误。这时候需要把公式改为:
\Gamma(s)=\int_{1\times10^{-10}}^{\frac{\pi}{2}-1\times10^{-10}}\mathrm{e}^{-\mathrm{tan}\ x}(\mathrm{tan}\ x)^{s-1}(1+\mathrm{tan}^2x)\mathrm{d}x\ \ (0<s<1)
例如计算:
\Gamma(0.5)=\sqrt{\pi}\approx1.772453851
\Gamma(0.6)=1.489192249
按照上面的算式则有:
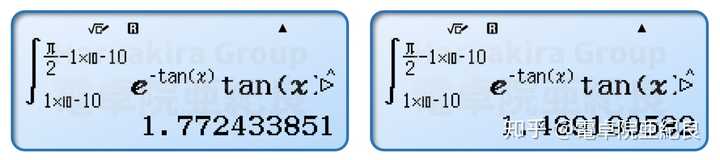
这里我们注意到在 0<s<1 的时候可能会出现较小的误差,那么我们还可以根据Gamma函数的性质 \Gamma(s+1)=s\Gamma(s) ,按照前面的方法来计算 0<s<1 时候的Gamma函数。
例如计算 \Gamma(0.6) ,先计算 \Gamma(1.6) ,然后再计算 \frac{\Gamma(1.6)}{0.6} :

这样就得到更精确的结果了。
