Attention+积分梯度=归因解释新方法：AAAI2021 Best Paper Runners Up

在上面的文章中，我们认为： 相比attention score作为输入归因，使用梯度信息或者擦除对预测的影响作为输入归因在理论和实践中都有更好的表现。

没有想到这么快就有新的结论了——这一篇来自AAAI2021的Best Paper Runners Up就使用了attention相关的归因方法（ 当然，重点在于attention的显著性信息 ）：

全文小结

这篇文章提出的 注意力归因图 （Attention Attribution Graph）方法为transformer的注意力层求梯度显著性作为注意力归因，然后将不同层的注意力归因作为带权边构造词依赖图：

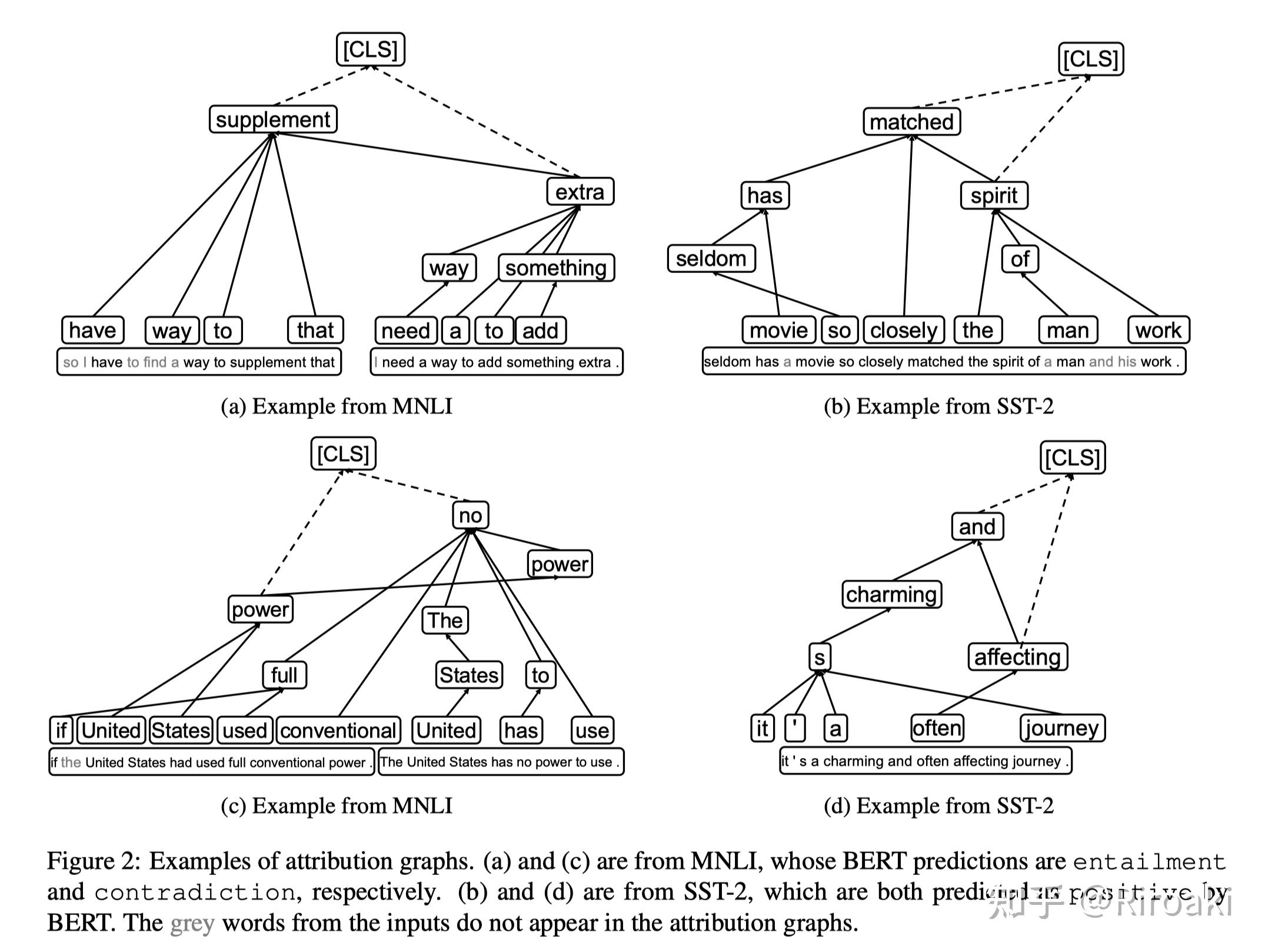
在提出了方法的基础上，作者进行了验证和拓展实验有：

1. 剪枝attention head ：并通过将attention heads按attribution sum作为重要性剪枝，和现有模型剪枝方法进行比较，经验性地证明了这一方法获得的归因图最好地保留了模型的信息流动；
2. 错误模式挖掘 ：通过归因图的可视化，可以发现模型对某些pattern的异常依赖——这些模式可以用于生成 对抗 样本，结合对抗样本，可以展示模型预测中的问题并针对性训练以调整之，从而提高模型的泛化能力。

总体而言，个人认为本文的亮点在于 提出了新方法，整合了注意力解释和显著性解释两个方法的优势：

• Attention由于属于模型的一部分，可以通过修改和剪枝对模型预测过程进行 主动干预 ，从而验证重要性的判断，这一点对于显著性方法这种事后解释而言是难以实现的；
• Attention可以 建模输入词对彼此的交互和依赖关系 ，当然，局部的依赖是没有什么意义的，因此作者考虑了全部层的attention attribution，并且构建了 全局的依赖图 ；
• 由于attention score被证明无法提供输入的重要性解释，采用了积分梯度这一显著性方法，它克服了简单梯度的饱和（saturation）现象，能够很好地反映输入（即attention） 对输出的影响程度 而不受其值影响，这一点作为归因图的边权重。

以下内容将介绍本文的算法和实验结果，文末有个人对本文的详细评价（指挑刺）。

注意力归因

我们之前的文章（上面的链接）提到，注意力权重不能反映输入重要性，而基于梯度的显著性信息能够反映重要性却无法表示输入的交互依赖。于是本文就提出了一种结合二者的方案：对每一层的注意力权重求梯度显著性，这就是注意力归因（Attention Attribution，ATTATTR）。

首先，我们回顾一下transformer中的多头注意力机制（multi-head attention）。

单头注意力的计算为：

H_{h}=\text { AttentionHead }(X)=A_{h} V_{h}=\operatorname{softmax}\left(\frac{Q_{h} K_{h}^{\top}}{\sqrt{d_{k}}}\right)V_{h}.(1)

那么多头注意力的计算为：

\operatorname{MultiH}(X)=\left[H_{1}, \cdots, H_{|h|}\right] W^{o}.(2)

其中 |h| 表示注意力头的个数， [\cdot] 表示向量拼接， W^{o} \in \mathbb{R}^{|h| d_{v} \times d_{x}} 。

接下来，我们按照积分梯度的方法，对第 h 个注意力头，按如下计算其归因矩阵（积分梯度即对输入在基线值到当前值的路径上求梯度的积分，在之前的文章中有介绍）：

\begin{aligned} A &=\left[A_{1}, \cdots, A_{|h|}\right] \\ \operatorname{Attr}_{h}(A) &=A_{h} \odot \int_{\alpha=0}^{1} \frac{\partial \mathrm{F}(\alpha A)}{\partial A_{h}} d \alpha \in \mathbb{R}^{n \times n} \end{aligned}.(3)

其中 \odot 为点乘， A_h \in \mathbb{R}^{n \times n} 表示第 h 个注意力头的注意力权重矩阵（同式（1））， \alpha 代表线性插值的权重，当其值为0时代表所有token间的attention权重为0。这样一来，计算结果既考虑了attention权重，同时也包含了输出对这一层attention权重的敏感程度。

当然，我们无法直接计算积分，只能用黎曼和近似求解归因值矩阵：

\operatorname{Attr}_{h}(A)=\frac{A_{h}}{m} \odot \sum_{k=1}^{m} \frac{\partial \mathrm{F}\left(\frac{k}{m} A\right)}{\partial A_{h}}.(4)

其中 m 为近似的步数，文章中设置为20。

下面可以看到，单个注意力归因图显然比其权重图更加稀疏：

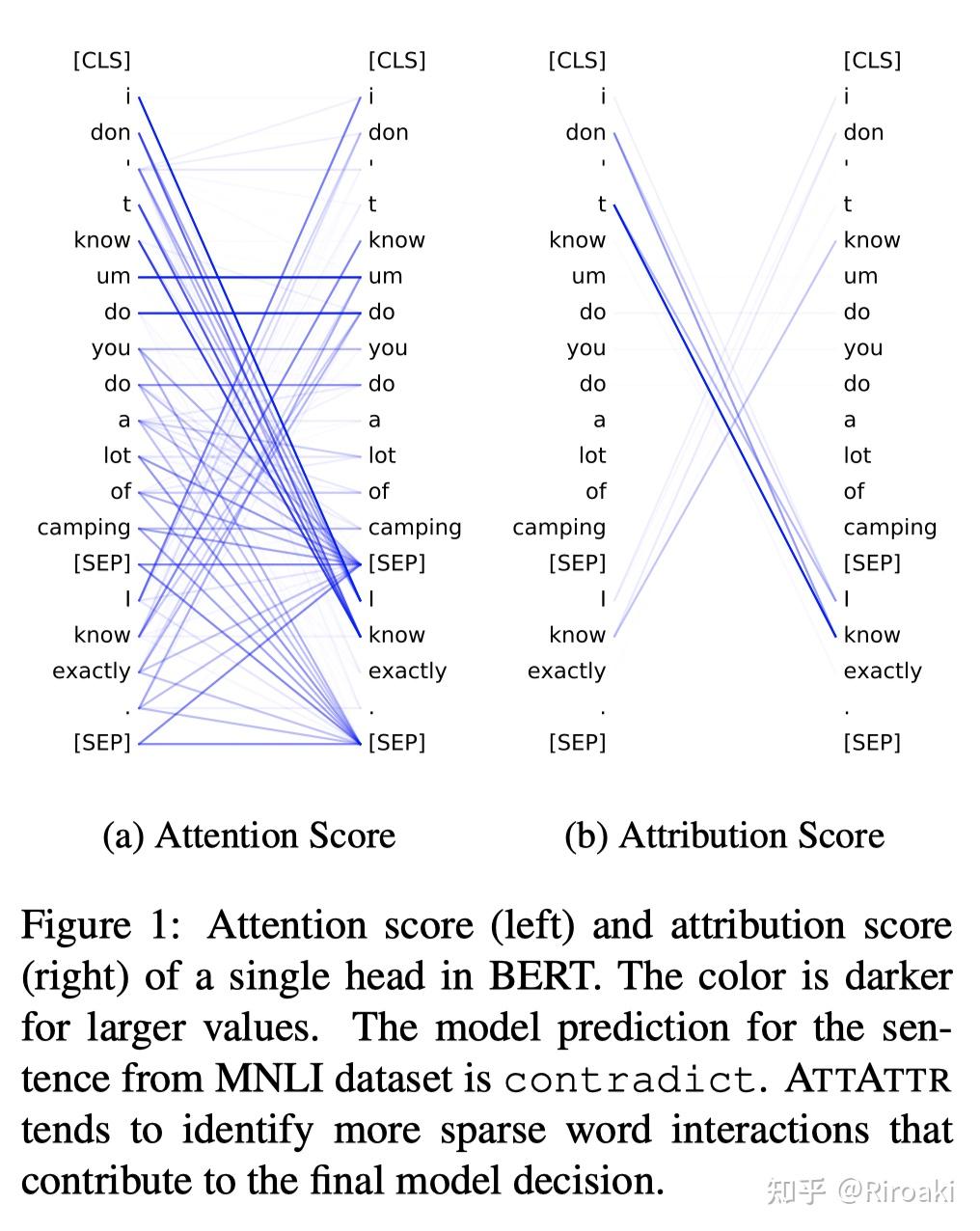
归因图构造算法

在计算单层的注意力权重归因以后，本文设计了一种注意力归因图构造算法，将各层的注意力归因作为词依赖边的权重，进行图的构造，并使用构造的图作为一种可视化方法来分析模型学到的句子内词的依赖关系。

具体思路和过程如下：

1. 将各层的注意力归因按头相加作为该层的注意力归因： \operatorname{Attr}\left(A^{l}\right)=\sum_{h=1}^{|h|} \operatorname{Attr}_{h}\left(A^{l}\right)=\left[a_{i, j}^{l}\right]_{n \times n}.(5) ；
2. 按照（1）最大化归因图中边权重的和，以及（2）最小化归因图中边的数量进行图的构造。这一目标形式上表达为： \text { Graph }=\underset{\left\{E^{l}\right\}_{l=1}^{|l|}}{\arg \max } \sum_{l=1}^{|l|} \sum_{(i, j) \in E^{l}} a_{i, j}^{l}-\lambda \sum_{l=1}^{|l|}\left|E^{l}\right|,\\ E^{l} \subset\left\{(i, j) \mid \frac{a_{i, j}^{l}}{\max \left(\operatorname{Attr}\left(A^{l}\right)\right)}>\tau\right\}.(6)
1. 其中 |E^l| 为第 l 层的边数量， \lambda 为两个目标取舍的权重， \tau 用于过滤出相对较大的注意力归因值，实验中为0.4。
3. 由于上面的组合优化问题难以解决，这里采用一种启发式的自顶向下的方法来构造图，基于以下几个 原则 ：
1. 按从后往前构造图，即层数从大到小；
2. 每个节点都有自连边，因为transformer中有残差连接；
3. 信息流动中，重复边和反向边应该被去除；
4. 如果[SEP]为叶节点（即，没有出现从[SEP]出发指向其它token的边），就在图中忽略它，毕竟这个token只是一个特殊标记而不包含语义信息。

根据上面的原则，设计了如下算法：

概括一下，就是从最后一层注意力归因出发，在每层找到权重较大的边（通过阈值 \tau 进行过滤，并去除已有的边和与已有边反向的边），最终合并各层的边形成完整的图。

看看效果图吧：

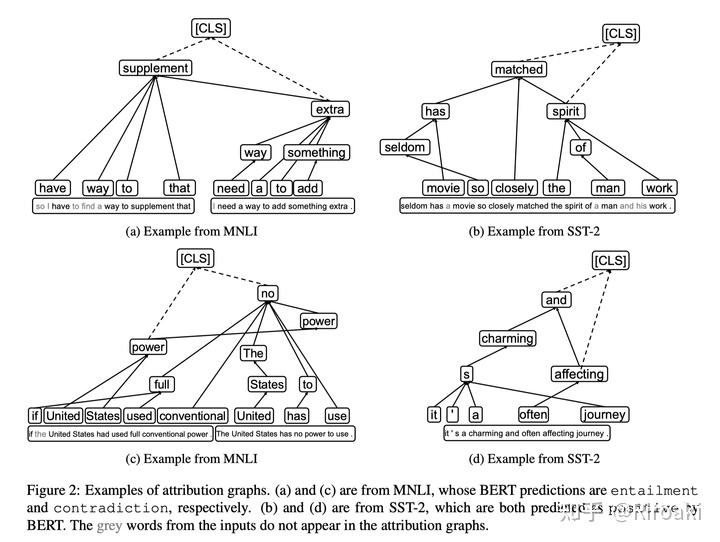
设计了归因图以后，自然需要验证它是否真的有效。case study就不必多言，文章中还通过注意力头剪枝的方法证明了注意力的归因值与其对模型预测的影响的相关性，以及ATTATTR方法的有效性。

有效性验证——注意力头剪枝（1）

这里主要分为两点。

首先是按归因值大小（降序或者升序）对各层注意力头进行剪枝，下图中可以看到按归因值升序剪枝中间竟然出现了效果提升的现象？图中也按注意力值升序和降序进行剪枝实验，结论显然是：注意力值大小对模型预测没什么影响。

对这个剪枝我有点疑惑，是对所有测试样本统一的剪枝方式吗？还是对每个样本针对性地剪枝不同的注意力头呢……而且按归因值升序剪枝，acc竟然不降反升？有必要验证一下……

第二点，探究不同层attention attribution反映出的感受野（Receptive Field）。这一部分没有得出什么结论，更高的层具有更大的感受野，这是显然的……

有效性验证——注意力头剪枝（2）

本文进一步细化了剪枝的实验，提出了按重要性剪枝的方法。注意力头重要性的定义如下：

I_{h}=E_{x}\left[\max \left(\operatorname{Attr}_{h}(A)\right)\right].(7)

其中， x 来自验证集， \max (\operatorname{Attr}_{h}(A)) 表示该头最大的注意力归因值。

这里，作为参考进行比较的还有基于精确度差（accuracy difference）和泰勒展开（Taylor Expansion）作为重要性的剪枝方法（参考：2019，arxiv，《Are sixteen heads really better than one?》）。

按重要性从低到高剪枝，对模型表现的影响如下：

看起来，基于ATTATTR归因的重要性更能保留模型中重要的信息流动（其实和泰勒展开差不多……）。

那么，对于不同任务和数据集（或者说领域domain），这种重要性是否一致？本文也进行了相关性分析，从下图中可以看到，RTE、MRPC和MNLI都具有很大的相关性，RTE、MRPC和SST-2相关性很低，而RTE、MRPC和MNLI都是2句分类的任务，区别在于一个和MNLI是同领域，一个不同，而SST-2是单句分类任务。

这说明，基于归因值的注意力头重要性只跟 任务类型 有关，和数据是否同领域无关。

ATTATTR方法提供了层次化的归因解释，从解释中我们可以发现模型判断的非正常依赖——这一点表现在对某些重复出现的句子特征的记忆等，对于真正理解语义是有害的。我们可以借此构造对抗样本来训练和提升模型的泛化性能。

对抗样本生成

这里通过每个句子中最大的归因值找出有明显依赖的词对，并将此用于构造对抗性触发词（Adversarial Triggers），将其插入到正常文本中干扰原始预测，生成对抗样本，如下图：

这里构造trigger的方式参考了2019，EMNLP，《Universal adversarial triggers for attacking and analyzing NLP.》

具体的实验设计中，从3k句子中抽取了trigger，每个trigger包含不超过5个token，并且具有一个分数，即其中每个token的归因值平均值。在SST-2中，注意避开了具有明显情感倾向的词（具体做法是列黑名单～）

我有两点疑惑：（1）这里显然插入了两个不同的词对（trigger）才成功实现了attack。是不是说明只插入一对词的影响不大呢？（2）这里的插入位置具体是怎么确定的呢？总不会是人工确认吧……这一部分在文章里也没有详细介绍：（

实验结果如下：

结论

• 本文提出了一种基于注意力归因（ATTATTR）的解释方法，这一方法可以解释transformer模型内部的信息交互，并使得注意力方法具有更好的解释性。
• 本文进一步提出了注意力归因图的构造算法，归因图展示了模型内部的信息流动。
• 然后文章提出了量化的分析方法验证ATTATTR算法的有效性，并用它标记出了重要的注意力头，提出了一种新的剪枝方法。
• 最后，本文提出了一种对抗方法，根据注意力归因发现的重要依赖构造对抗性的trigger，构造新的对抗样本。

个人评价（姑妄言之）

本文的思路上，采用剪枝方法验证经验上的合理性，实现了自圆其说（目前领域内对生成的解释还没有比较合理的指标）；应用上，提出模型对模式（指trigger）的依赖和构造对抗样本，属于锦上添花，对后续工作具有一定的指导意义。

个人认为本文存在的不足之处有：

• 实验细节存在缺失 ——剪枝部分内容有一些细节没有详细阐述，对抗样本生成的过程也比较简单， 但是这部分本该是需要详细说明，并且和其他方法进行对比的 。
• 归因图的构造算法比较依赖直觉 ——如果像《Axiomatic Attribution for Deep Networks》中提出公理并给出数学证明一样那将绝杀，可惜换不得；
• 基于阈值的方法比较经验 ，文章里没有说 \tau=0.4 是怎么取的，为什么不取0.3，0.5或者其他数值；
• 实验可以更全面 ，看完全文似乎主要只对文本分类（SST-2，MRPC）和文本推理（MNLI，RTE），但这不影响本文的质量，属于后续工作。
• transformer模型除了multi-head attention部分以外，还有feed-forward network部分，因而归因图其实没有覆盖模型内全部的信息流动。当然，这一点实验效果说了算：）

后记

• 不能再偷懒了……摸鱼好几个月都没有产出
• 新一年考研形势如此激nei烈juan，似乎已经看到自己两年后毕业即失业的惨状LOL