使用JS实现图（1）——概述

1 年前 · 来自专栏使用JavaScript描述数据结构

柯醪德

我马上就要从那一团乱麻中出来了

图的算法难度较大，对于图的不同存储结构，其将对程序的效率产生相当大的影响，所选的存储结构应适合于要求解的问题。无论是有向图还是无向图，图的主要存储结构都有两种：邻接矩阵和邻接表。

邻接表属于图的链式存储结构，本系列实现图的算法时采用的存储结构就是它。

邻接表对图中每个顶点都建立一个单链表，第 i 个单链表中的节点表示依附于顶点 Vi 的边，对于有向图则是以顶点 Vi 为尾的弧，这个单链表就成为顶点 Vi 的边表。所以在邻接表中存在两种节点：顶点表节点和边表节点。

顶点表节点结构如下：

// 顶点表节点
class Vertex {
    constructor(data) {
        this.data = data; // 顶点域
        this.firstEdge = null; // 指向第一个邻接边的指针
        this.outNum = 0;  // 在无向图中表示与顶点邻接的边的数量，在有向图中为出度
        this.inNum = 0;  // 在有向图中为顶点的入度

data记录顶点节点的数值，firstEdge则指向当前顶点的边表中的第一个节点。outNum在无向图中表示的是与顶点邻接的边的数量，在有向图中则是出度。inNum在无向图中没有意义，在有向图中表示顶点的入度。

边表节点结构如下：

// 边表节点
class Edge {
    constructor(data, weight = 0, nextEdge = null) {
        this.data = data; // 邻接点域
        this.nextEdge = nextEdge; // 指向下一条邻接边
        this.weight = weight;  // 权重

data为数据域，nextEdge则是指向与顶点 Vi 相邻的下一个节点。weight表示顶点 Vi 到当前节点的权重。

举例如下：

若有无向图

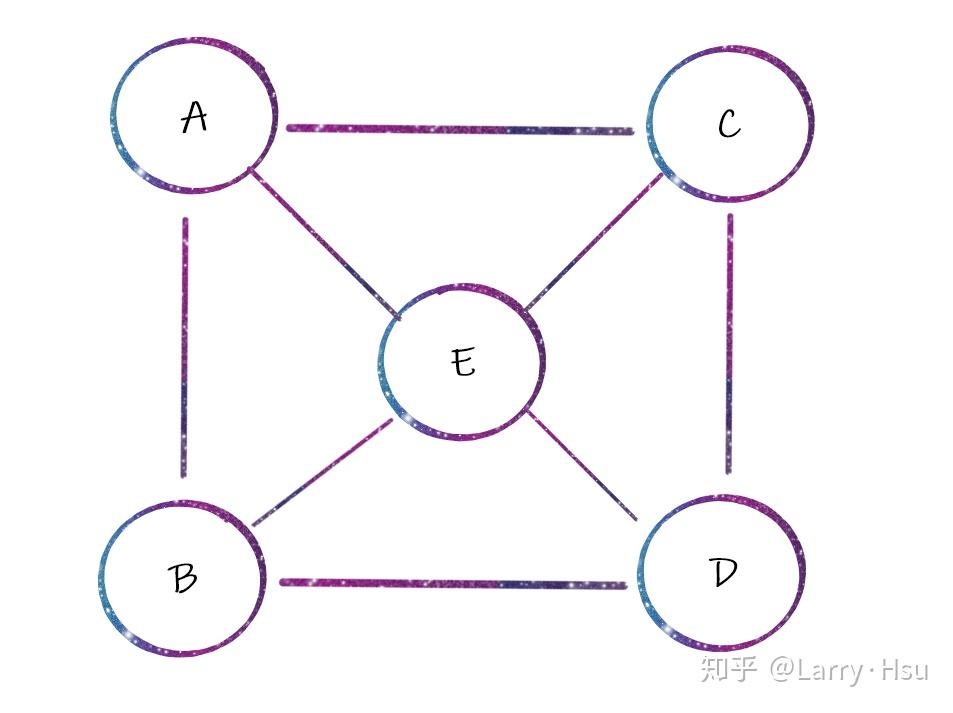
则该图的邻接表表示如下：

对图的重要的操作都有：

insertVertex(x)  // 向图中插入新的顶点
allNeightbors(x)  // 与顶点x邻接的所有节点
addEdge(x, y, w = 0)  // 向图中插入边(x, y)
removeEdge(x, y)  // 在图中删除边(x, y)
deleteVertex(x)  // // 从图中删除顶点x
hasEdge(x, y)  // 判断是否存在边(x,y)或者<x, y>
getAllEdge()  // 获取图中所有的边
getEdgeWeight(x, y)  // 获取边(x, y)或<x, y>对应的权值
getMaxEdgeWeight()  // 获得图中最大的权值
getMinEdgeWeight() // 获得图中最小的权值
setEdgeWeight(x, y, w)  // 设置边(x, y)或<x, y>的权值
BFSTraverse(x)  // 广度优先遍历
DFSTraverse(x)  // 深度优先遍历