List<int> insertionSort(List<int> list) {
if (list.length < 2) return list;
for (var i = 1; i < list.length; i++) {
for (var j = i; j > 0 && list[j] > list[j - 1]; j--) {
swap(list, j, j - 1);
return list;
原理:构建一个已经排序的序列,然后从未排序的序列里依次取出元素并插入到已排序序列的合适位置。
运作过程:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5
总结:不占用额外的内存空间,但是由于在插入元素时,为了给新元素提供空间,需要不断的扫描已排序序列并将元素依次移动。
插入排序 VS 选择排序
插入排序和选择排序很像,从第一个元素开始,都是先排出一个有序序列,然后从后面无序序列里取出元素。不同点在于:
选择排序仰仗”比较“,插入排序更受制于“交换”:选择排序是遍历无序序列,并从中取出最大或最小的元素(不断的比较);插入排序是遍历有序序列,将无序序列的第一个元素插入到有序序列的合适位置(不断的交换元素)。
插入排序是稳定的(如果a原本在b前面,而a=b,排序之后a仍然在b的前面)。
由于插入排序是将元素插入到有序序列的合适位置,一旦找到了合适位置,就可以结束当前循环(越是有序的序列,它所需要的时间越少)。而选择排序是从无序序列里寻找最大(最小)的元素,必须完整的遍历序列。所以,在原始序列就比较有序的情况下,插入排序相比于选择排序效率会高很多。
插入排序和比较排序谁更优?
同等条件优先选择插入排序
如果比较开销>>交换开销:选择插入排序
如果比较开销<<交换开销:选择选择排序
其他情况两者差别不大,但一般情况下,插入排序确实优于选择排序
List<int> shellSort(List<int> list) {
if (list.length < 2) return list;
for (var gap = list.length ~/ 2; gap > 0; gap ~/= 2) {
for (var i = gap; i < list.length; i++) {
for (var j = i; j >= gap && list[j] > list[j - gap]; j -= gap) {
swap(list, j, j - gap);
return list;
原理:希尔排序可以理解为是一种优化后的插入排序。上一节插入排序VS选择排序,我们可知道,如果一个数组本来就相对比较有序,那么插入排序的销量会提高很多。而希尔排序正是利用这一特性。使用一个增量对序列进行分组,并分别使用插入排序,然后不断的循环缩减增量,直至增量为1,而此时,序列已经是一个相对比较有序的序列了。
总结:由于增量序列的存在,它不再是稳定的。但是其销量有了质的提升。
List<int> mergeSort(List<int> list) {
if (list.length < 2) return list;
var left = list.sublist(0, list.length ~/ 2);
var right = list.sublist(list.length ~/ 2);
return _mergeSortMerge(mergeSort(left), mergeSort(right));
List<int> _mergeSortMerge(List<int> left, List<int> right) {
var merge = List<int>(left.length + right.length);
var leftIndex = 0;
var rightIndex = 0;
var mergeIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] >= right[rightIndex]) {
merge[mergeIndex++] = left[leftIndex++];
} else if (left[leftIndex] < right[rightIndex]) {
merge[mergeIndex++] = right[rightIndex++];
while (leftIndex < left.length) {
merge[mergeIndex++] = left[leftIndex++];
while (rightIndex < right.length) {
merge[mergeIndex++] = right[rightIndex++];
return merge;
原理:一种建立在归并操作上的排序,是一个典型的分治算法。将数组不断的分割,直至只有一个元素,此时该数组是有序的。然后将有序的数组不断合并。
运作过程:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
总结:是一种稳定的排序算法,性能远胜于选择排序,但是需要额外的内存空间。
在看快速排序之前,看一下一个分组排序:
List<int> groupSort(List<int> list) {
if (list.length < 2) return list;
var chosenNum = list[Random().nextInt(list.length)];
var small = <int>[];
var same = <int>[];
var large = <int>[];
for (var i = 0; i < list.length; i++) {
if (list[i] > chosenNum) {
large.add(list[i]);
} else if (list[i] < chosenNum) {
small.add(list[i]);
} else {
same.add(list[i]);
if (small.isNotEmpty) {
small = groupSort(small);
if (large.isNotEmpty) {
large = groupSort(large);
return large..addAll(same)..addAll(small);
原理:通过选定一个目标值,然后将小于、等于它以及大于它的元素分别放在三个不同的数组里,然后不断的遍历数组,直至最后无元素可遍历后在合并数组。
快速排序正式利用这一原理——选定一个目标值,找到所有比它大(小)的元素,就能确定目标值在数组中所处的位置(index)。但是这个排序明显需要引入额外的内存空间。
将它优化后就是快速排序
List<int> quickSort(List<int> list) {
if (list.length < 2) return list;
_quickPartition(list, 0, list.length - 1);
return list;
int _pivotIndex(int min, int max) {
var i = min + Random().nextInt(max - min);
return i;
void _quickPartition(List<int> list, int low, int height) {
if (low < height) {
swap(list, _pivotIndex(low, height), height);
var pivot = list[height];
var i = (low - 1);
for (var j = low; j < height; j++) {
if (list[j] >= pivot) {
swap(list, i, j);
var targetPoint = i + 1;
swap(list, targetPoint, height);
_quickPartition(list, low, i);
_quickPartition(list, i + 2, height);
原理:通过一次遍历,根据目标值将数组分成两个部分。分割完毕后可确定目标值的位置,然后再分别对分割后的两个部分进行排序。
总结:也是一种分治策略,是一种不稳定的排序。
List<int> heapSort(List<int> list) {
if (list.length < 2) return list;
var len = list.length - 1;
var beginIndex = list.length~/2 - 1;
for (var i = beginIndex; i >= 0; i--) {
_maxHeapify(i, len, list);
for (var i = len; i > 0; i--) {
swap(list,0, i);
_maxHeapify(0, i - 1,list);
return list;
void _maxHeapify(int index, int len, List<int> list) {
var li = 2*index + 1;
var ri = li + 1;
var cMin = li;
if (li > len) return;
if (ri <= len && list[ri] < list[li]) {
cMin = ri;
if (list[cMin] < list[index]) {
swap(list, cMin, index);
_maxHeapify(cMin, len, list);
原理:一种利用堆进行排序的算法,堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
通常通过一维数组来实现堆。在数组起始位置为0的情形中:
父节点i的左子节点在位置2i+1
父节点i的右子节点在位置2i+2
子节点i的父节点在位置(i-1)/2
运作过程:
最大堆调整:将堆的末端子节点作调整,使得子节点永远小于父节点
创建最大堆:将堆中的所有数据重新排序
堆排序:移除位在第一个数据的根节点,并做最大堆调整的递归运算
更详细的堆排序请参考详解二叉堆和堆排序
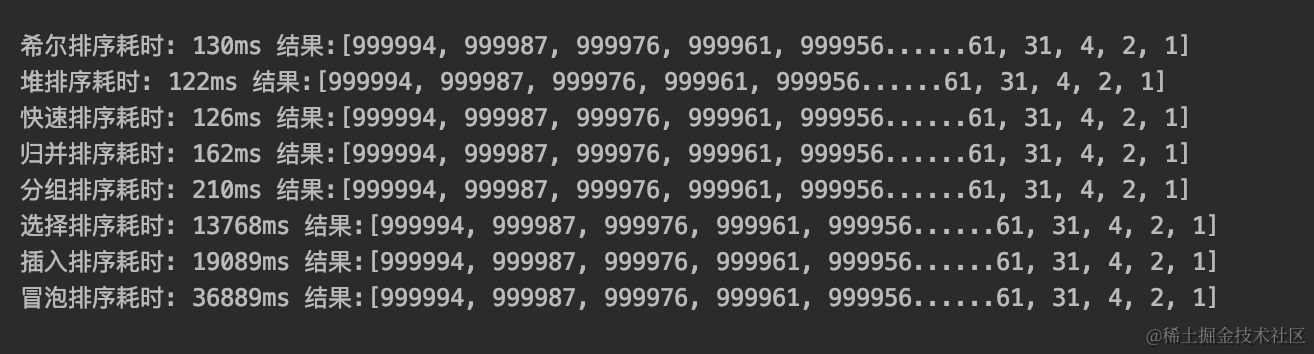
源码和效果展示
Dart排序算法
运行代码:
void main() {
var rng = Random();
var originalList = List<int>(99999);
for (var i = 0; i < originalList.length; i++) {
originalList[i] = rng.nextInt(999999
);
Isolate.spawn(execution, MethodMessage('冒泡排序', bubbleSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('选择排序', selectionSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('插入排序', insertionSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('希尔排序', shellSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('归并排序', mergeSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('分组排序', groupSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('快速排序', quickSort, List.of(originalList)));
Isolate.spawn(execution, MethodMessage('堆排序', heapSort, List.of(originalList)));
while (true) {}