[Notes]用pomegranate进行贝叶斯网络结构学习
译自 Bayesian Network Structure Learning
author: Jacob Schreiber
contact: jmschreiber91@gmail.com
由于两个主要原因,学习贝叶斯网络的结构可能很复杂:(1)推断因果关系的困难和(2)数据集中超指数的有向边可能性。 当结构学习算法仅考虑相关性或其他共现度量来确定边(edge)是否应该存在时,就会出现第一个问题。 第一点是值得深思的挑战,但与 pomegranate 的实现无关;本教程将重点关注如何用pomegranate实现快速贝叶斯网络结构学习。它还将涵盖一个称为“约束图”的新概念,该概念可用于大幅加速结构搜索,同时使因果关系分配更加合理。
一句话总结
# 从数据中学习结构
model = BayesianNetwork.from_samples(X)
# 可选参数:
# algorithm,选择优化算法,'exact-dp'最短路径算法,'exact'A*算法,默认贪婪搜索,'chow-liu'Chow-Liu树算法,
# constraint_graph, 传入networkx.DiGraph对象作为约束图加速优化
# weights,默认1,可置任意非负数,为各样本加权
# pseudocount,默认0,起平滑作用?
# max_parents, 最大父节点数贝叶斯网络结构学习简述
大多数贝叶斯网络结构学习(BNSL)方法可以归为以下三类之一:
(1) 搜索和评分(Search and Score):
最直观的方法是“搜索和评分”,其中搜索所有可能的有向无环图 (DAG) 的空间,并确定最小化某个目标函数的那个。典型的目标函数试图平衡给定模型的数据的对数概率(似然)与模型的复杂性,以鼓励更稀疏的模型。这种搜索的幼稚实现随着变量的数量在时间上是超指数的,并且在考虑不到十几个变量时变得不可行。然而,动态规划可以有效地消除许多重复计算,并将其减少为简单的时间指数。这允许精确的 BNSL 扩展到 ~25-30 个变量。此外,A* 算法可用于智能搜索空间并通过甚至不考虑所有可能的网络来进一步减少计算时间。
(2) 约束学习(Constraint learning):
这些方法通常涉及计算一些相关性或共现的度量,以识别可能存在的无向边主干,然后系统地修剪这些边,直到达到 DAG。一种常见的方法是迭代所有三元组变量以识别指定边缘存在和方向的条件独立性。该算法比搜索和评分算法渐近(时间上是二次的),但它没有简单的概率解释。
(3) 近似算法(Approximate algorithms):
在许多现实世界的例子中,人们希望将搜索和评分方法的可解释性与在宇宙结束之前完成任务的吸引力相结合。为此,已经开发了几种具有不同属性的启发式方法,以在合理的时间内产生良好的结构。这些方法包括 Chow-Liu 树构建算法、爬山算法和最优重新插入,但还有其他方法。
pomegranate中的结构学习
Exact learning(Search and Score)
【case01】从samples建立贝叶斯网
pomegranate中的结构学习是使用 from_samples 方法完成的。 您传入的只是(1)样本;(2)权重;(3)算法;它将使用动态规划实现为您学习网络。 让我们看一个示例,以确保找到合适的连接。 让我们在变量 1、3、6 和变量 0 和 2 以及变量 4 和 5 之间添加连接。
from pomegranate import BayesianNetwork
import seaborn
import numpy as np
seaborn.set_style('whitegrid')
# pomegranate自带的model.plot()方法有问题,需要自己重新写一个
def plot(model):
import pygraphviz
import tempfile
import matplotlib.pyplot as plt
import matplotlib.image as matimg
G = pygraphviz.AGraph(directed=True)
for state in model.states:
G.add_node(state.name, color='red', shape='circle')
for parent, child in model.edges:
G.add_edge(parent.name, child.name)
with tempfile.NamedTemporaryFile() as tf:
G.draw(tf, format='png', prog='dot')
img = matimg.imread(tf)
plt.imshow(img)
plt.axis('off')
plt.show()
# 构造一个200行7列的samples,列0、2相关,列1、3、6相关,列4、5相关
X = np.random.randint(2, size=(200, 7))
X[:,3] = X[:,1]
X[:,6] = X[:,1]
X[:,0] = X[:,2]
X[:,4] = X[:,5]
# 从samples建立贝叶斯网
model = BayesianNetwork.from_samples(X, algorithm='exact')
# 结构打出来看下,画个节点图
print(model.structure)
plot(model)
输出为
((), (), (0,), (1,), (), (4,), (3,))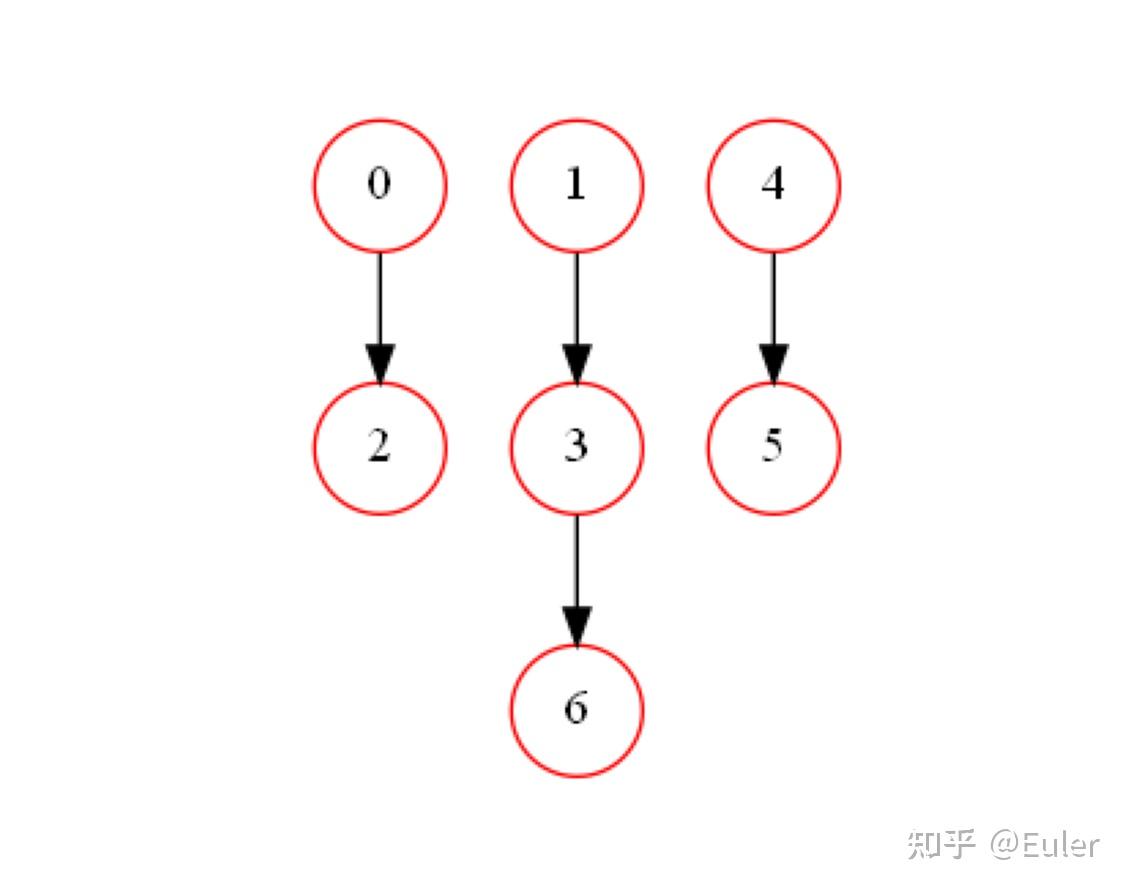
结构属性返回一个二维tuple,其中每个内部元组对应于节点,该内部元组中的数字对应于该节点的父节点。此输出的含义是,节点 3 有节点 1 作为父节点,节点 2 有节点 0 作为父节点,依此类推。该结果切实地重新捕获了数据中的底层依赖关系。
【case02】算法效率比较:Shortest Path VS A* Search
有两种执行搜索和评分的算法,传统的 最短路径算法 和 A* 算法 。这两者的工作原理都是将贝叶斯网络结构学习问题转化为有序图上的最短路径问题。这个顺序图是由来自 BNSL 问题的变量集层组成的格子,根节点没有变量,叶节点有所有变量,格子中的层 i 具有大小为 i 的变量的所有子集。每条从根到叶的路径代表变量的某种拓扑排序,最短路径对应最优拓扑排序和贝叶斯网络。详细信息可以在 这里 找到。传统的最短路径算法在找到最短路径之前计算顺序格中所有边的值,而A*算法只搜索顺序格的一个子集并立即开始搜索。这两种方法都会产生 最佳的 贝叶斯网络结构。
传统最短路径算法中出现的一个主要问题是有序图的大小随着变量的数量呈指数增长,并且会使具有其他合理计算时间的任务变得不可行。A* 算法在计算上更快,且使用更少的内存,因为它不探索全部有序图,因此可以应用于更大规模的问题。
为了在实践中看到这些算法之间的差异,让我们转向在手写数字集(MNIST)上学习贝叶斯网络的任务。数字数据集由超过一千张 8x8 的手写数字图片组成。为简单起见,我们将值二值化为“开”或“关”:
from pomegranate import BayesianNetwork
from sklearn.datasets import load_digits
import numpy as np
import matplotlib.pyplot as plt
import time
X, y = load_digits(n_class=10, return_X_y=True)
X = X > np.mean(X)
plt.figure(figsize=(14, 4))
plt.subplot(131)
plt.imshow(X[0].reshape(8, 8), interpolation='nearest')
plt.grid(False)
plt.subplot(132)
plt.imshow(X[1].reshape(8, 8), interpolation='nearest')
plt.grid(False)
plt.subplot(133)
plt.imshow(X[2].reshape(8, 8), interpolation='nearest')
plt.grid(False)
plt.show()
并尝试学习像素之间的依赖关系:
# 取了每张图像的前18个像素学习其依赖关系,这个例子其实没啥实际意义
X = X[:, :18]
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact-dp')
t1 = time.time() - tic
p1 = model.log_probability(X).sum()
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact')
t2 = time.time() - tic
p2 = model.log_probability(X).sum()
print("Shortest Path")
print("Time (s): ", t1)
print("P(D|M): ", p1)
print()
print("A* Search")
print("Time (s): ", t2)
print("P(D|M): ", p2)运行结果:
Shortest Path
Time (s): 42.78771615028381
P(D|M): -8267.950447476833
peak memory: 2234.61 MiB, increment: 1932.45 MiB
A* Search
Time (s): 25.080483198165894
P(D|M): -8267.950447476833
peak memory: 860.71 MiB, increment: 552.22 MiB这些结果表明,与传统算法相比,A* 算法在计算上更快,而且需要的内存要少得多,使其成为“精确”算法的更好默认值。 BNSL 进程使用的内存量在“增量”下,而不是“峰值内存”,因为“峰值内存”返回所有内容使用的总内存,而增量显示函数运行前后峰值内存的差异。
【case03】算法比较:Approximate Learning: Greedy Search (pomegranate default)
当非贪婪算法太慢时,一种自然的启发式方法是考虑贪婪版本。这个简单的例子迭代地找到要添加到不断增长的拓扑排序的最佳变量,允许新变量仅从拓扑排序中的变量中提取。 这是 pomegranate 的默认设置,因为它在生成好的(通常是最佳的)图形和具有较小的计算成本和内存占用之间取得了很好的平衡。 但是,不能保证这会产生全局最优图。在上一问题中,其表现如下:
tic = time.time()
model = BayesianNetwork.from_samples(X) # << Default BNSL setting
t = time.time() - tic
p = model.log_probability(X).sum()
print("Greedy")
print("Time (s): ", t)运行结果:
Greedy
Time (s): 1.4977431297302246
P(D|M): -8434.745069065655
peak memory: 216.68 MiB, increment: 0.07 MiB【case04】算法比较:Approximate Learning: Chow-Liu Trees
然而,甚至存在贪婪启发式太慢的情况,例如数百个变量。 BNSL 的最好的启发式方法之一是 Chow-Liu 树,它从数据中学习最佳树。本质上它计算所有变量对之间的互信息,然后找到最大生成树。必须输入根节点才能将基于互信息的无向边转换为贝叶斯网络的有向边。该算法是 $O(d^{2})$ 并且实际上非常快且内存效率极高,尽管它产生的结构具有更差的 $P(D|M)$。同一问题的表现:
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='chow-liu') # << Default BNSL setting
t = time.time() - tic
p = model.log_probability(X).sum()
print("Chow-Liu")
print("Time (s): ", t)
print("P(D|M): ", p)运行结果:
Chow-Liu
Time (s): 0.045445919036865234
P(D|M): -8752.32666094451
peak memory: 190.02 MiB, increment: 0.00 MiB【case05】算法横评 | Comparison
扩展要考虑的像素数量,可以直接在MNIST上相互比较算法:
from pomegranate import BayesianNetwork
from sklearn.datasets import load_digits
import numpy as np
import matplotlib.pyplot as plt
import time
X, _ = load_digits(n_class=10, return_X_y=True)
X = X > np.mean(X)
# 数据集太大了算半天,就取前100个来算吧
X = X[:100]
print(X)
# 分别记录4种算法在不同问题规模下的时间消耗与对数概率和
t1, t2, t3, t4 = [], [], [], []
p1, p2, p3, p4 = [], [], [], []
n_vars = range(8, 19)
# 尝试8—18的11个不同规模的例子
for i in n_vars:
X_ = X[:,:i]
tic = time.time()
model = BayesianNetwork.from_samples(X_, algorithm='exact-dp')
t1.append(time.time() - tic)
p1.append(model.log_probability(X_).sum())
tic = time.time()
model = BayesianNetwork.from_samples(X_, algorithm='exact')
t2.append(time.time() - tic)
p2.append(model.log_probability(X_).sum())
tic = time.time()
model = BayesianNetwork.from_samples(X_, algorithm='greedy')
t3.append(time.time() - tic)
p3.append(model.log_probability(X_).sum())
tic = time.time()
model = BayesianNetwork.from_samples(X_, algorithm='chow-liu')
t4.append(time.time() - tic)
p4.append(model.log_probability(X_).sum())
plt.figure(figsize=(14, 4))
plt.subplot(121)
plt
.title("Time to Learn Structure", fontsize=14)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.ylabel("Time (s)", fontsize=14)
plt.xlabel("Variables", fontsize=14)
plt.plot(n_vars, t1, c='c', label="Exact Shortest")
plt.plot(n_vars, t2, c='m', label="Exact A*")
plt.plot(n_vars, t3, c='g', label="Greedy")
plt.plot(n_vars, t4, c='r', label="Chow-Liu")
plt.legend(fontsize=14, loc=2)
plt.subplot(122)
plt.title("$P(D|M)$ with Resulting Model", fontsize=14)
plt.xlabel("Variables", fontsize=14)
plt.ylabel("logp", fontsize=14)
plt.plot(n_vars, p1, c='c', label="Exact Shortest")
plt.plot(n_vars, p2, c='m', label="Exact A*")
plt.plot(n_vars, p3, c='g', label="Greedy")
plt.plot(n_vars, p4, c='r', label="Chow-Liu")
plt.legend(fontsize=14)
plt.show()
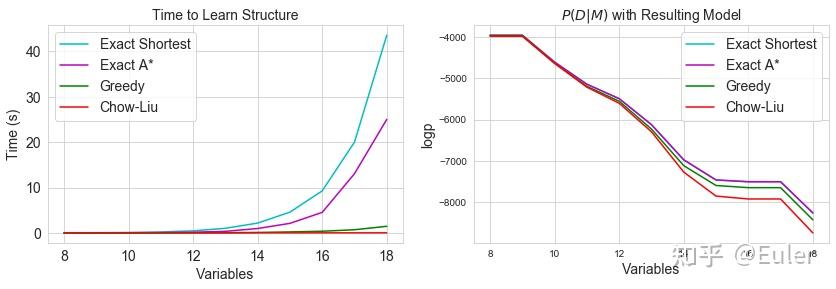
我们可以看到预期的结果——A* 算法比最短路径更快,贪心算法比最短路径更快,Chow-Liu 算法最快。 紫色和青色线叠加在右图上,因为它们生成具有相同分数的图形,紧随其后的是贪心算法,然后是 Chow-Liu 表现最差。
【case06】约束图 | Constraint Graphs
现在,有时您有关于节点组如何相互连接的 先验信息 ,并希望利用它。 这可以采用全局排序的形式,例如,变量可以以这样的方式排序,即有向边只能从左到右。 但是,有时您的网络中有层,其中变量是这些层的一部分,并且只能在另一层中有父层:
from pomegranate import BayesianNetwork, DiscreteDistribution, ConditionalProbabilityTable, Node
import matplotlib.pyplot as plt
BRCA1 = DiscreteDistribution({0: 0.999, 1: 0.001})
BRCA2 = DiscreteDistribution({0: 0.985, 1: 0.015})
LCT = DiscreteDistribution({0: 0.950, 1: 0.050})
OC = ConditionalProbabilityTable([[0, 0, 0, 0.999],
[0, 0, 1, 0.001],
[0, 1, 0, 0.750],
[0, 1, 1, 0.250],
[1, 0, 0, 0.700],
[1, 0, 1, 0.300],
[1, 1, 0, 0.050],
[1, 1, 1, 0.950]], [BRCA1, BRCA2])
LI = ConditionalProbabilityTable([[0, 0, 0.99],
[0, 1, 0.01],
[1, 0, 0.20],
[1, 1, 0.80]], [LCT])
PREG = DiscreteDistribution({0: 0.90, 1: 0.10})
LE = ConditionalProbabilityTable([[0, 0, 0.99],
[0, 1, 0.01],
[1, 0, 0.25],
[1, 1, 0.75]], [OC])
BLOAT = ConditionalProbabilityTable([[0, 0, 0, 0.85],
[0, 0, 1, 0.15],
[0, 1, 0, 0.70],
[0, 1, 1, 0.30],
[1, 0, 0, 0.40],
[1, 0, 1, 0.60],
[1, 1, 0, 0.10],
[1, 1, 1, 0.90]], [OC, LI])
LOA = ConditionalProbabilityTable([[0, 0, 0, 0.99],
[0, 0, 1, 0.01],
[0, 1, 0, 0.30],
[0, 1, 1, 0.70],
[1, 0, 0, 0.95],
[1, 0, 1, 0.05],
[1, 1, 0, 0.95],
[1, 1, 1, 0.05]], [PREG, OC])
VOM = ConditionalProbabilityTable([[0, 0, 0, 0, 0.99],
[0, 0, 0,
1, 0.01],
[0, 0, 1, 0, 0.80],
[0, 0, 1, 1, 0.20],
[0, 1, 0, 0, 0.40],
[0, 1, 0, 1, 0.60],
[0, 1, 1, 0, 0.30],
[0, 1, 1, 1, 0.70],
[1, 0, 0, 0, 0.30],
[1, 0, 0, 1, 0.70],
[1, 0, 1, 0, 0.20],
[1, 0, 1, 1, 0.80],
[1, 1, 0, 0, 0.05],
[1, 1, 0, 1, 0.95],
[1, 1, 1, 0, 0.01],
[1, 1, 1, 1, 0.99]], [PREG, OC, LI])
AC = ConditionalProbabilityTable([[0, 0, 0, 0.95],
[0, 0, 1, 0.05],
[0, 1, 0, 0.01],
[0, 1, 1, 0.99],
[1, 0, 0, 0.40],
[1, 0, 1, 0.60],
[1, 1, 0, 0.20],
[1, 1, 1, 0.80]], [PREG, LI])
s1 = Node(BRCA1, name="BRCA1")
s2 = Node(BRCA2, name="BRCA2")
s3 = Node(LCT, name="LCT")
s4 = Node(OC, name="OC")
s5 = Node(LI, name="LI")
s6 = Node(PREG, name="PREG")
s7 = Node(LE, name="LE")
s8 = Node(BLOAT, name="BLOAT")
s9 = Node(LOA, name="LOA")
s10 = Node(VOM, name="VOM")
s11 = Node(AC, name="AC")
model = BayesianNetwork("Hut")
model.add_nodes(s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11)
model.add_edge(s1, s4)
model.add_edge(s2, s4)
model.add_edge(s3, s5)
model.add_edge(s4, s7)
model.add_edge(s4, s8)
model.add_edge(s4, s9)
model.add_edge(s4, s10)
model.add_edge(s5, s8)
model.add_edge(s5, s10)
model.add_edge(s5, s11)
model.add_edge(s6, s9)
model.add_edge(s6, s10)
model.add_edge(s6, s11)
model.bake()
plt.figure(figsize=(14, 10))
# pomegranate自带的model.plot()方法有问题,需要自己重新写一个
def plot(model):
import pygraphviz
import tempfile
import matplotlib.pyplot as plt
import matplotlib.image as matimg
G = pygraphviz.AGraph(directed=True)
for state in model.states:
G.add_node(state.name, color='red', shape='circle')
for parent, child in model.edges:
G.add_edge(parent.name, child.name)
with tempfile.NamedTemporaryFile() as tf:
G.draw(tf, format='png', prog='dot')
img = matimg.imread(tf)
plt.imshow(img)
plt.axis('off')
plt.show()
plot(model)
plt.show()
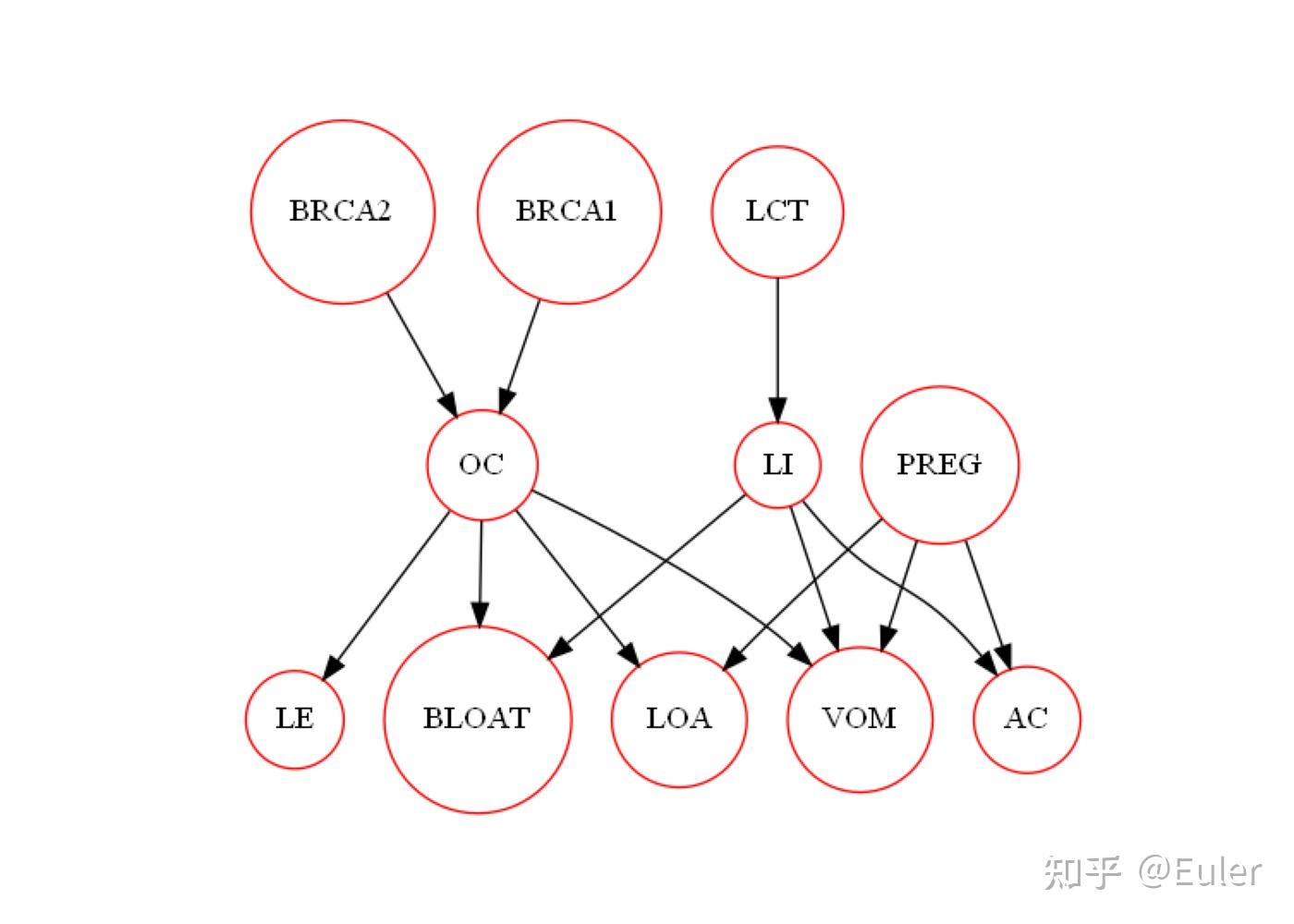
这个图包含三层:
- 底层:症状,低能量、腹胀、食欲不振、呕吐和腹部绞痛;
- 中间:疾病,上皮癌、乳糖不耐症和怀孕;
- 顶层:三种不同的基因突变检测结果;
该图中的边是受约束的:基因突变可以解释疾病,疾病可以解释症状(因可以解释果)。而从疾病到遗传条件、从遗传条件到症状都没有边缘(果不能导致因)。如果我们要设计一种更有效的搜索算法,我们会希望利用 这一事实 (网络的分层结构)来大幅减少图的搜索空间。
在提出解决方案之前,让我们还考虑另一种情况:在某些情况下,您可以定义变量的 全局排序 ,这意味着您可以从左到右对它们进行排序,并确保边缘仅从左到右(前因→后果)。这可以代表一些时间分离(左侧的事情发生在右侧的事情之前)、物理分离或其他任何事情。这也将大大减少搜索空间。
除了减少搜索空间之外,一种有效的算法可以利用这种分层结构。大多数评分函数的一个关键特性是 全局参数独立性(global parameter independence) 的思想:假设节点 A 的父节点与节点B的父节点独立,则AB在图中不形成环。如果您有一个分层结构,例如在诊断网络中或通过全局排序,则不可能通过父值的任何有效分配在图中形成一个循环。这意味着可以独立识别每个节点的父节点,从而大大减少算法的运行时间。
现在,有时我们知道一些关于变量结构的事情,但对其他的一无所知。 例如,我们可能对某些变量有偏序,但对其他变量一无所知。 我们可以对其他人强制执行任意排序,但这可能没有充分的理由。 本质上, 我们想利用我们拥有的任何信息 。
抽象地,我们可以从约束图的角度考虑这一点。 假设您有一些症状、疾病和基因测试,并且先验地不知道所有这些部分之间的联系,但您确实知道之前的层结构。 您可以定义一个“约束图”,它由“症状”、“疾病”和“基因突变”三个节点组成。 从基因突变到疾病有一个有向边,从疾病到症状有一个有向边。 这说明基因突变可以是疾病的根源,疾病可以是症状的根源。 它看起来像下面这样:
import networkx
constraints = networkx.DiGraph()
constraints.add_edge('genetic conditions', 'diseases')
constraints.add_edge('diseases', 'symptoms')
# pomegranate的plot_networkx方法也有问题,得自己写
def plot_networkx(networkx):
import pygraphviz
import tempfile
import matplotlib.pyplot as plt
import matplotlib.image as matimg
G = pygraphviz.AGraph(directed=True)
for edge in networkx.edges():
G.add_edge(edge[0], edge[1])
with tempfile.NamedTemporaryFile() as tf:
G.draw(tf, format='png', prog='dot')
img = matimg.imread(tf)
plt.imshow(img)
plt.axis('off')
plt.show()
plot_networkx(constraints)
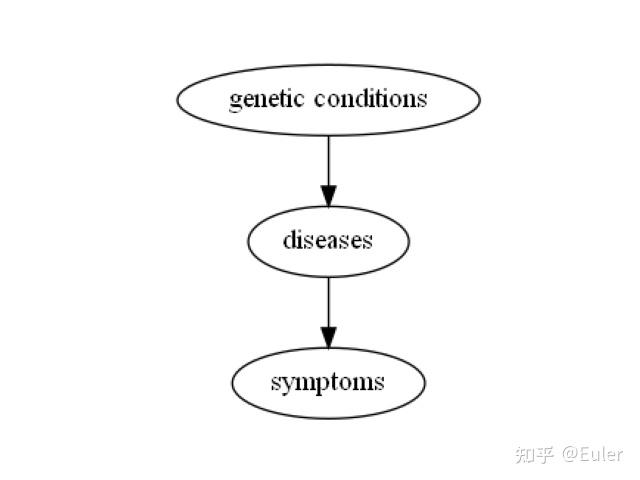
与这些类别相对应的所有变量都将放在其适当的名称中。 这将为结构学习定义一个脚手架。现在,我们可以对全局排序做同样的事情。 假设我们有 3 个变量,按 0-2 的顺序排列:
constraints = networkx.DiGraph()
constraints.add_edge(0, 1)
constraints.add_edge(1, 2)
constraints.add_edge(0, 2)
plot_networkx(constraints)
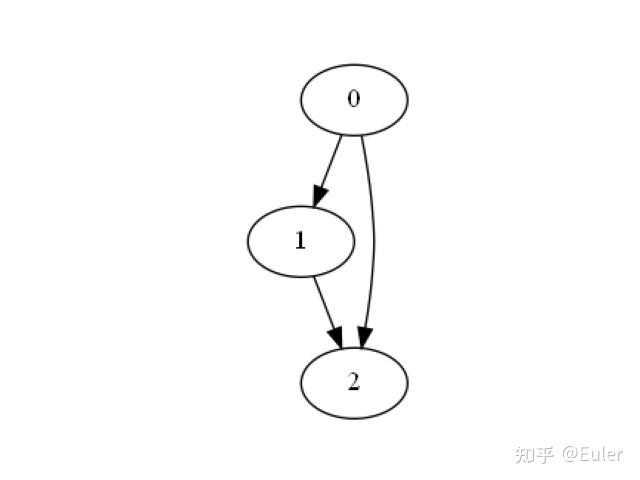
在这个图中,我们说:变量 0 可以是 1 或 2 的父级,变量 1 可以是变量 2 的父级。 就像将多个变量放在一个节点中,约束图的允许我们定义层,将单个变量放在约束图的层(节点)中可以让我们定义排序。
具体来说,节点 1 中包含的变量,其父项只能来自节点 0 。我们可以从节点0包含的变量中,独立地为节点 1 中的每个变量找到最佳父集。这比试图找到节点 0 和 1 中所有变量的最佳贝叶斯网络要快得多!我们也可以通过遍历节点 0 和 1 中的变量来对节点 2 中的变量做同样的操作,为节点 2 中的变量找到最佳父集。
但是,在某些情况下,我们对某些变量的父结构一无所知。这可以通过在图中包含自循环来解决,即该节点是它自己的父节点。这意味着我们对该节点中变量的父结构一无所知,并且必须运行完整的指数时间算法。 朴素结构学习算法可以被认为是将所有变量放在约束图中的单个节点中,并在该节点上放置一个自循环。
因此,我们剩下两个程序;一种用于求解属于自边的边,另一种用于求解不是自边的边。即使我们必须对具有自循环的节点中的变量使用指数时间过程,它仍然会明显更快,因为我们将使用更少的变量(朴素问题除外)。
通常,即使我们没有关于所有节点的信息,我们也会有关于图中某些节点的一些信息。假设我们知道某些变量没有子变量但可以有父变量,而对其他变量一无所知:
constraints = networkx.DiGraph()
constraints.add_edge(0, 1)
constraints.add_edge(0, 0)
plot_networkx(constraints)
在这种情况下,我们必须对节点 0 中的变量运行指数时间算法以找到最佳父节点,然后对节点 1 中的变量运行独立父节点算法,仅从节点 0 中的变量中提取。 具体来说:
- 使用指数时间过程在节点 0 的变量中找到最优结构;
- 使用独立父程序在节点 1 中找到变量的最佳父节点,限制父节点位于节点 0 ;
- 连接这些父集一起得到给定约束的网络的最优结构。
我们可以将其推广到任何任意约束图:
- 使用指数时间过程在具有自循环的节点(如果需要,包括来自其他节点的父节点)的变量间找到最佳结构;
- 使用独立父节点过程在给定父节点约束的情况下找到节点中变量的最佳父节点必须来自作为该节点父节点的节点中的变量;
- 将这些父集连接在一起以获得给定约束的网络的最佳结构。
根据贝叶斯网络的全局参数独立性,该过程将在探索网络的显著较小部分的同时给出全局最优的贝叶斯网络。
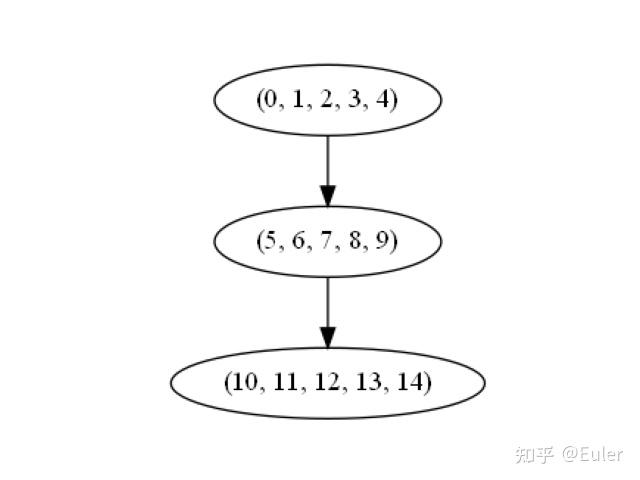
pomegranate 以极其易于使用的方式支持约束图。假设我们有一个像诊断模型这样的三层图,每层有五个变量。我们可以将约束图定义为 networkx DiGraph,节点为元组、包含所有归属于此节点的变量id。
设定 (0, 1, 2, 3, 4) 是第一个节点, (5, 6, 7, 8, 9) 是第二个节点, (10, 11, 12, 13 , 14) 是最终节点:
import numpy as np
import networkx
import matplotlib.pyplot as plt
import time
from pomegranate import BayesianNetwork
# pomegranate自带的model.plot()方法有问题,需要自己重新写一个
def plot(model):
import pygraphviz
import tempfile
import matplotlib.pyplot as plt
import matplotlib.image as matimg
G = pygraphviz.AGraph(directed=True)
for state in model.states:
G.add_node(state.name, color='red', shape='circle')
for parent, child in model.edges:
G.add_edge(parent.name, child.name)
with tempfile.NamedTemporaryFile() as tf:
G.draw(tf, format='png', prog='dot')
img = matimg.imread(tf)
plt.imshow(img)
plt.axis('off')
plt.show()
# pomegranate的plot_networkx方法也有问题,得自己写
def plot_networkx(networkx):
import pygraphviz
import tempfile
import matplotlib.pyplot as plt
import matplotlib.image as matimg
G = pygraphviz.AGraph(directed=True)
for edge in networkx.edges():
G.add_edge(edge[0], edge[1])
with tempfile.NamedTemporaryFile() as tf:
G.draw(tf, format='png', prog='dot')
img = matimg.imread(tf)
plt.imshow(img)
plt.axis('off')
plt.show()
# 构造数据
np.random.seed(6)
X = np.random.randint(2, size=(200, 15))
X[:,1] = X[:,7]
X[:,12] = 1 - X[:,7]
X[:,5] = X[:,3]
X[:,13] = X[:,11]
X[:,14] = X[:,11]
# 创建约束图
a = networkx.DiGraph()
b = tuple((0, 1, 2, 3, 4))
c = tuple((5, 6, 7, 8, 9))
d = tuple((10, 11, 12, 13, 14))
a.add_edge(b, c)
a.add_edge(c, d)
print("Constraint Graph")
plot_networkx(a)
plt.show()
print("Learned Bayesian Network")
# 使用约束图
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact', constraint_graph=a)
plt.figure(figsize=(16, 8))
plot(model)
plt.show()
print("pomegranate time: ", time.time() - tic, model.structure)
# 不使用约束图
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact')
plt.figure(figsize=(16, 8))
plot(model)
plt.show()
print("pomegranate time: ", time.time() - tic, model.structure)约束图:
让变量 1、7 和 12 相关,11、13、14 相关,以及 3 和 5 相关。在这种情况下,1、7、12应当连接,3、5应当连接,11、13 和 14 都是同一层的一部分因此应该忽略连接:
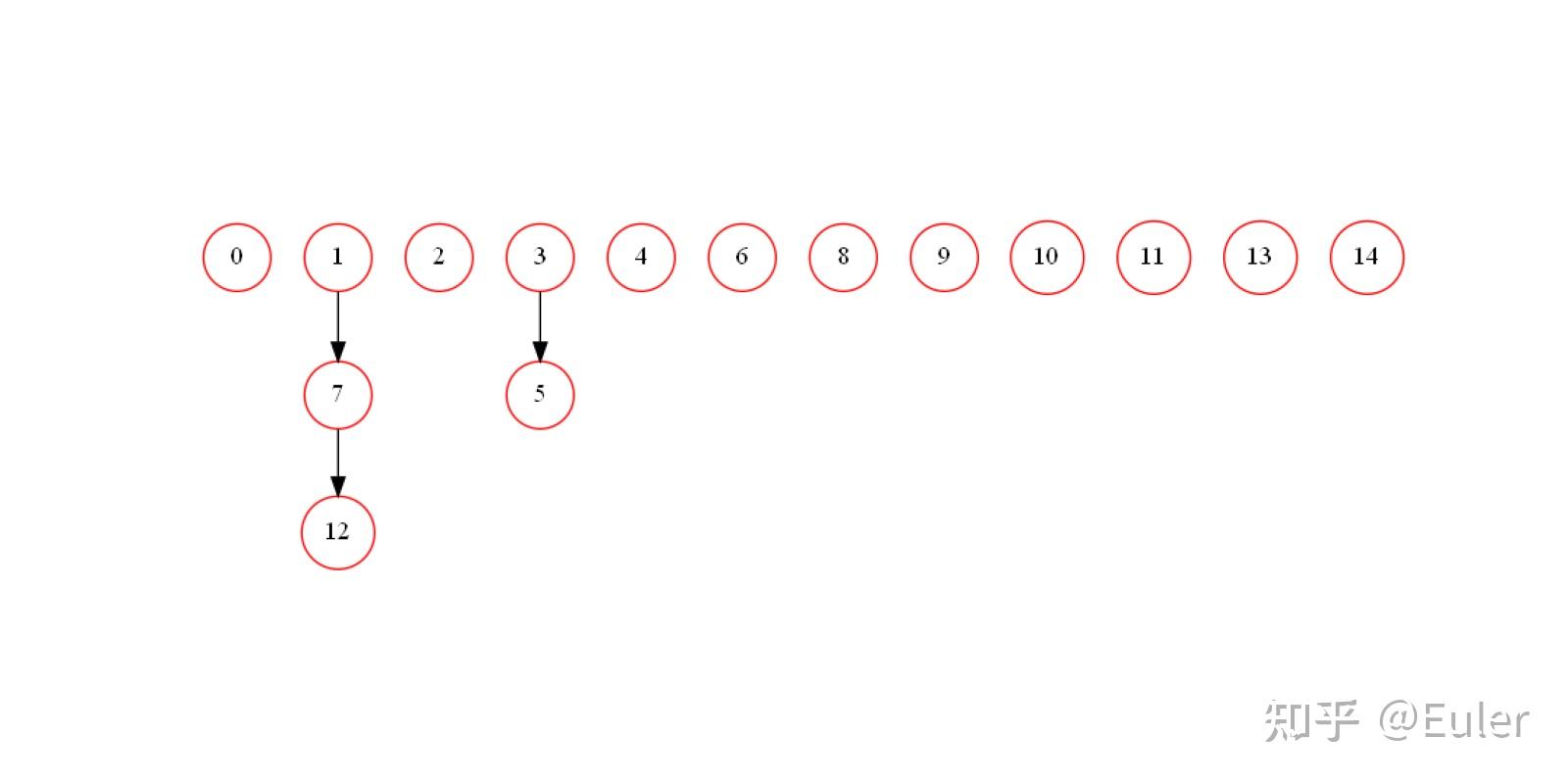
结果被完美地重建了;
如果不使用约束图会如何呢?
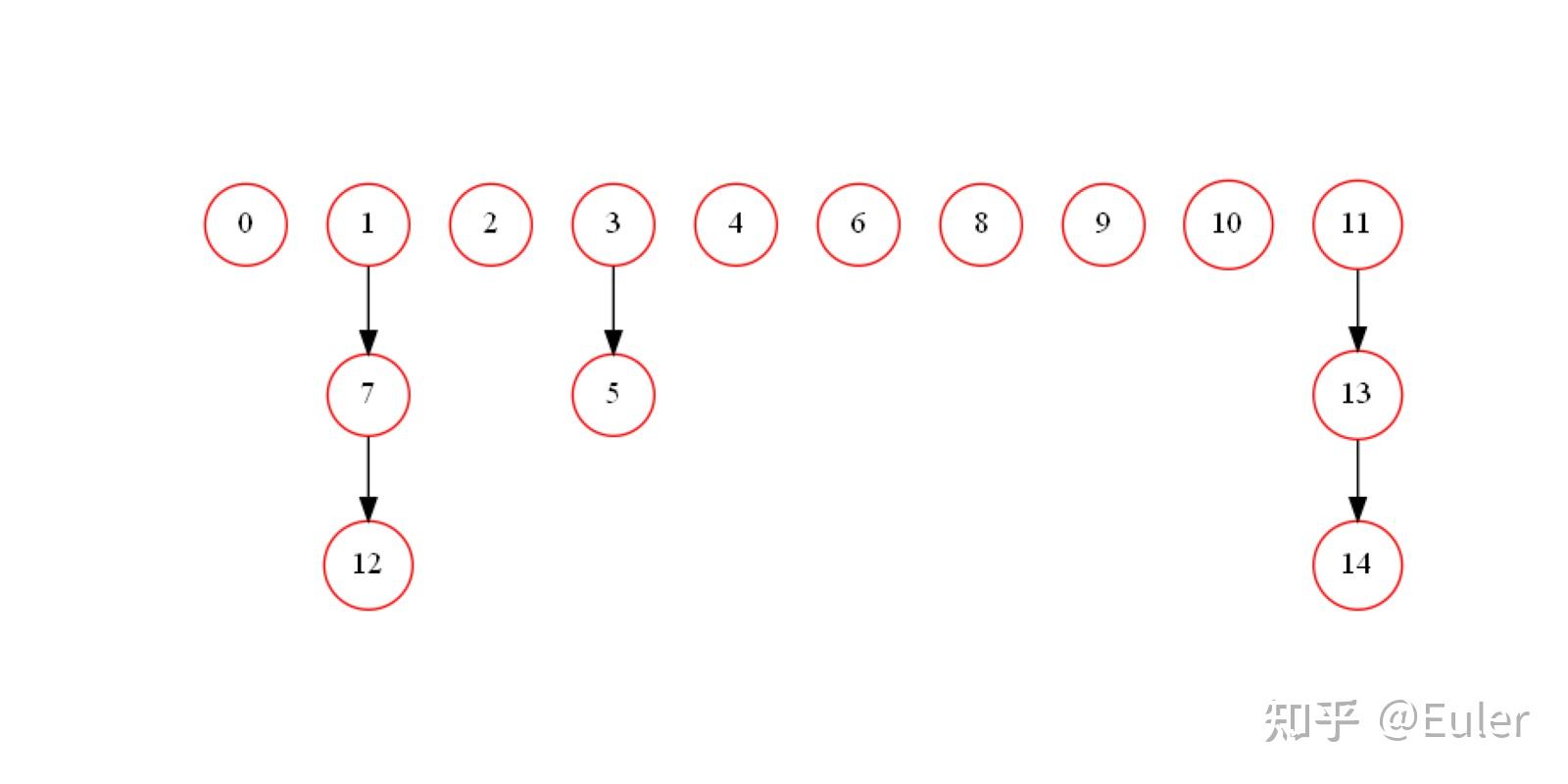
看起来我们通过使用约束图获得了三个理想的属性:
- 首先是在寻找最佳图时 速度提高了一个数量级 ;
- 在最终的贝叶斯网络中去 除一些我们不想要的边 ,例如 11、13 和 14 之间的边。我们还去除了 1 到 12 和 1 和 3 之间的边,对于我们最初定义的模型它们是错误的;
- 可以 指定一些边的方向 以得到更好的因果模型。
import matplotlib.pyplot as plt
import networkx, time, numpy, seaborn
from pomegranate import BayesianNetwork
seaborn.set_style('whitegrid')
constraint_times, times = [], []
x = numpy.arange(1, 7)
for i in x:
symptoms = tuple(range(i))
diseases = tuple(range(i, i * 2))
genetic = tuple(range(i * 2, i * 3))
constraints = networkx.DiGraph()
constraints.add_edge(genetic, diseases)
constraints.add_edge(diseases, symptoms)
X = numpy.random.randint(2, size=(100, i * 3))
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact', constraint_graph=constraints)
constraint_times.append(time.time() - tic)
tic = time.time()
model = BayesianNetwork.from_samples(X, algorithm='exact')
times.append(time.time() - tic)
plt.figure(figsize=(14, 6))
plt.title('Time To Learn Bayesian Network', fontsize=18)
plt.xlabel("Number of Variables", fontsize=14)
plt.ylabel("Time (s)", fontsize=14)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.plot(x * 3, times, linewidth=3, color='c', label='Exact')
