如何通俗地解释混沌理论(chaos)和分岔理论(bifurcation)?
11 个回答
一、何为分岔(bifurcation)?
有答主提到,分岔就是稳态数目的变化,我们可以从这里讲起。
我们知道,绝大多数的动力学系统可以用一组微分方程来表示:
\dot{\bold{y}}=\bold{L}\left( \lambda \right)\bold{y} - (1)
其中, y 是系统变量,一般而言,可以用系统的位置和动量表示。对于一个由N个粒子组成的经典系统,这是一个6N维度的向量。 L 是一个非线性算子,可以是方程组,也可以是微分算子(偏微分方程)。这个算子有一个参数λ,可以是m维的。典型的动力学方程例如哈密顿方程,薛定谔方程,化学反应的动力学方程,等等,都是这种形式。
一般而言,对于一个不受外界扰动的动力学系统,由于定律是不随着时间变化的,所以,L在这里不显含时间t。这称作自治系统(autonomous)。后续如果不明确说明,我们谈到的动力学方程都是自治的。
我们会关心当公式(1)等于零的时候:
\bold{L}\left( \lambda \right)\bold{y_0}=0 - (2)
此时,我们获得了一组常数解, y0 。很显然,不论系统的历史如何演化,它走过了什么样的轨迹然后才到达了这一点,我们可以确知的是,一旦它到了这一点,它就会保持不动 – 因为时间微分项已经变为零了。这样的点,我们称之为“ 不动点 ”。系统的不动点意味着系统达到了一个定常态,即系统不再随时间发生变化。
寻找不动点是相对比较容易的(当然仅仅是相对而言!),我们把微分方程(或偏微分方程)变成了代数方程(或常微分方程)。我这里略过偏微分方程的情况,因为它的分析思路与常微分方程并无二致。那么,方程(2) 有没有唯一解呢?答案是,不一定 。对于非线性方程,一般伴随着λ数值的变化,解的个数就会发生变化。比如说一个很简单的例子:
{L}\left( \lambda \right){y}=y^3+\lambda y=0
我们可以得到如下的解:
- 当λ>0时,方程有一个解,y=0
- 当λ<0时,方程有3个解,y=0,y=±√λ
我们把这个解随着参数变化情况画一个图
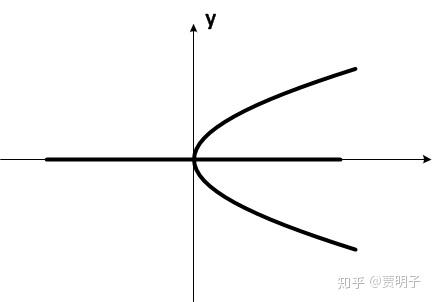
这个就是一个简单的分岔图。从这张图我们可以直观地体会到“分岔”这个名字的含义。这个图形的形状因为比较像一个草叉子,因而叫做 “草叉分岔”(pitchfork bifurcation) 。
这是一种最简单的、相对容易理解的分岔形式: 不动点的数量随着参数变化而变化 。然而在动力学系统中,“分岔”的含义更加丰富。
从动力学讲,我们可以非常简单地把“分岔”描述为这样一种现象,即 动力学系统的一个参数的连续变化却引起了系统行为突然的急遽反应,从而运动性质都变了 。庸俗一点说,就是“量变”引发了“质变”。这个我们后面还会更加详细描述。从一种运动模式变为另外一种运动模式,这种日常生活中很常见,也非常符合直观。比如说,有一根塑料直尺(如下图),如果我们在两边用力向内挤压,在用力较小的时候,直尺的状态除了微小的压缩形变之外不会有其他变化。但是当用力大到某一点时,直尺会突然被挤弯了。无论我们如何小心翼翼地缓慢加力,这种由直变弯的过程都是突然产生的。这种变换还有另外一种性质,即多值性:这种弯曲可能向上(A),也可能向下(B),并且,如果我们保证实验过程绝对不受外界扰动,它也可能仍然保持笔直(C),但是我们发现这种笔直的状态非常不稳定,轻轻一碰它就保持不住了。也就是说,这个直尺的可能状态由一开始的一个(笔直)变成了三个(上弯、下弯、笔直),同时伴随着稳定性的变化(弯曲是稳定状态,笔直是不稳定状态)。我们说,系统分岔了。
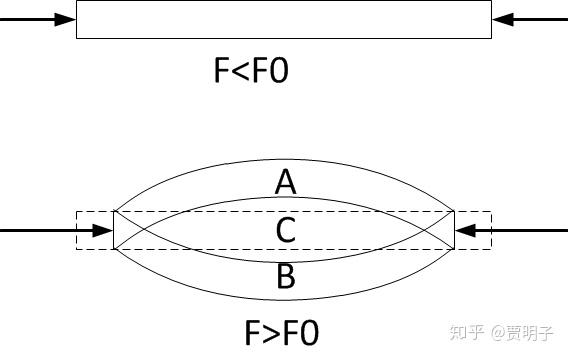
这里我们看到,分岔的几个基本特性:多值性,稳定性的变化,以及系统行为的突变。
上面的例子表明,一个参数的变化引起了系统运动模式的突然变化。当系统的参数连续不断变化的时候,有时会使得系统连续跨过多个分岔,它的复杂性每跨过一点都会以翻番的程度增加,并且分岔的出现也越来越频繁, 简化来讲,直到某一点,系统突然由规律变得不规律了,这时,系统就跨入了混沌。
我们再来从数学上讲,对公式(1)描述的动力学系统, 系统随着时间的演化过程可以表示为相空间中的一个点随时间变化而扫过的一条轨迹 (一个 流,“flow” )。关于这一点如果你不明白相空间和相图,请参考:
在相图中,一个不动点意味着一条轨迹的终点(或起点),因为系统一旦到达这一点之后,就不再变化,这个点也就静止不动了。
由公式(1)描述的动力学系统,我们总是从一个初始点开始来计算它的演化,每个初始点的演化过程都会有划出一条轨迹。所有不同初始点划出的轨迹的集合,就构成了相空间中的一个图形,称作相图。例如,一个单摆的动力系统相图如下:
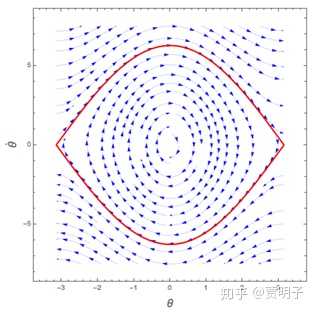
里面的每一个环形结构,对应着一个不同振幅的简谐振动。在红线外部,则是一些开放的轨迹,对应着回环摆。
从相图中,很容易就可以看到任何一个初始点对应的演化轨迹。算子L一旦确定,相应地整个空间流形的几何结构就确定了。L是随着参数λ变化的,所以因而显而易见的是,随着参数λ的变化,相空间的结构就会跟着变化。我们假设λ是连续变化的。当λ到达某些特定值时(奇异点),相空间里面的某些“平滑”的地方就会产生特殊的结构。诸如鞍点,结点,环,环面,等等,这些特殊结构的产生,就对应着系统的分岔。我们可以简单地讲,每种特殊结构都会改变系统的演化,于是发生系统运动模式的跳变。(图片来自网络, http://www. entropy.energy/scholar/ node/dynamical-systems-maps )
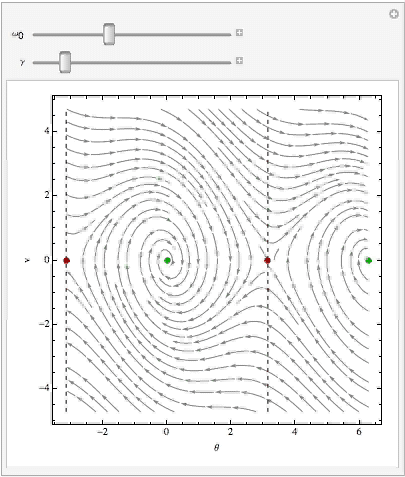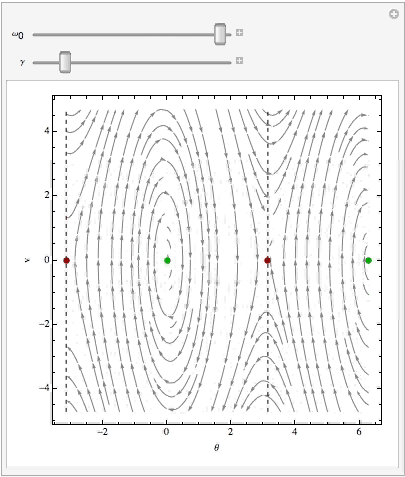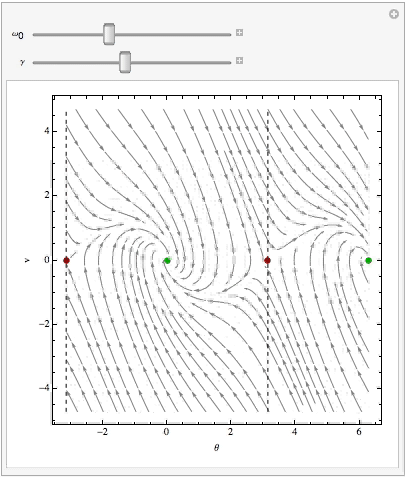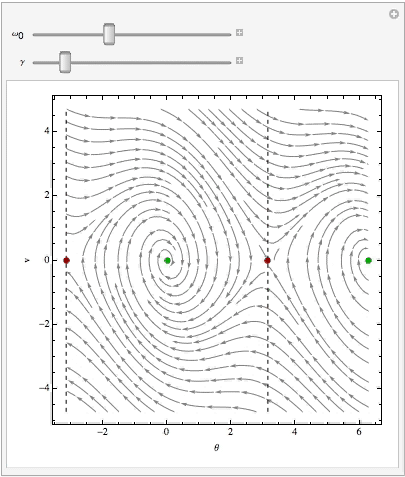
相图的任何几何结构(拓扑结构),我们可以用相图的形式直观地表示出来。前面讲到的不动点,就是一种特殊的几何结构:结点, 它是一组轨迹的终结点(或起点) 。此外,前面我们看到,相空间中的一个圆环就对应着一个震荡行为。此外还有很多。
这里多少提一句 拓扑结构 。其实,拓扑结构很容易从直观上理解,只是它研究的东西太“直观”,所以严格逻辑上的定义就显得过于抽象。 不太严格地讲,拓扑结构就是一些“柔软”的几何特性。 打个比方,你可以想象这个相图画在一个弹性的橡皮膜上面,你任意从各个方向上拉伸,挤压,扭曲,卷曲这个橡皮膜,它的几何形状虽然变化了,但是这个图形的“定性”性质,诸如各个结点的数量,线的连接方式,等等,却不会因此而改变,也就是说,它的拓扑结构不变(同胚)。如下图所示,通过一系列有限的连续拉伸,扭曲等形变,图形从A变成了B,数学上讲,这种形变可以表示为连续映射,那么A图形上的任意点都一一映射到B图形上,反之,B图形上的任一点也都一一映射到A图形上,即“互射”。但是,如果在相图中本来是一束流线的地方产生了一个结点,或者一个结点变成了一个环(图C),这种互射就被打破了,显然不能通过上述的“橡皮膜变换”得到,我们说那么它的拓扑结构就变了。
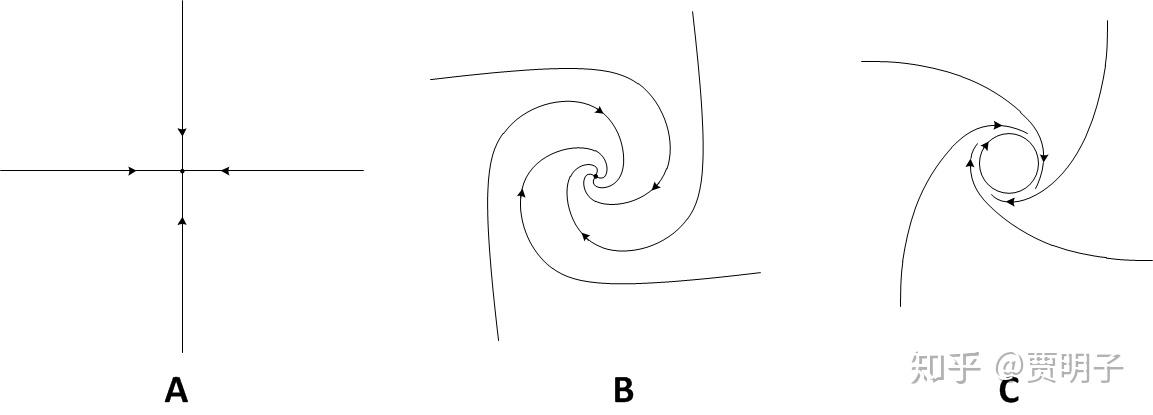
从动力学上我们可以这样解释这三张相图。A图中轨迹汇集到一个不动点,讲的是系统直接演化到一个稳态;B图中轨迹以螺旋线汇集到一个不动点,讲的是系统震荡收敛于一个稳态;C图中出现一个圆环结构,讲的是系统收敛于一个稳定的震荡。A和B的运动“大致”是一致的,它们都会收敛于一个稳态,但是C不同,C最终收敛于一个震荡。
所以说,分岔可以很严谨并且很简洁地这样定义:
分岔就是系统参数的变化引起了相空间的拓扑结构的变化,而此时参数点就叫做分岔点 。
也就是说,一个动力学系统的特性,可以由其相图表示。相图就是这样一种刻画动力学特性的“地图”。随着参数λ的变化,地图随之变化。当发生分岔的时候,就是地图的“定性性质”发生突变的时候。相应地,系统的运动模式就发生了跳变。
二、稳定性
前面在尺子的弯折的例子中,我提到分岔中最为至关重要的一个概念,稳定性。何为稳定性呢?从数学意义上来说的:
对于一个动力系统的定态,对它施加一个微小的扰动,系统对这个扰动的响应为△(t),如果我们有随着时间的推移,△趋向于零,那么,这个定态就是稳定的。
当然,从动力学上讲,有很多有意思的内涵,请参照:
那么,我们就以不动点为起点,来分析相空间里面的这些特殊点的几何结构到底是怎么样的,并且试图回答这些点到底是稳定的还是不稳定的。
混沌和分岔现象只能发生在不可积的非线性系统当中。由于非线性系统的复杂性,我们很难对它直接进行分析,常用的办法就是线性化。我们有定理可以保证,( Hartman & Grobmann定理 ),对非线性系统进行线性化,如果不在奇异点附近,则线性化的系统相空间的局部拓扑结构不变。那么在某一点我们把系统线性化:
\dot{\bold{y}}=\bold{L}\left( \lambda \right)\bold{y}=\bold{DL}\left( \bold{y_0},\lambda \right)\left( \bold{y-y_0} \right)+O\left( \bold{y-y_0} \right)^2
上式中, DL 是非线性算子的线性化。对于 L 是个非线性函数而言,它就是雅可比矩阵。
\bold{DL}\left( \bold{y_0},\lambda \right)=\frac{\partial \bold{L}\left( \lambda \right)}{\partial \bold{y}}\left( \bold{y_0} \right)=\bold{J}\left( \bold{y_0}, \lambda \right)
我们忽略高阶项,这就变成了一个线性系统。如前所述,如果满足如下前提:
1, 矩阵非奇异
2, 矩阵不存在纯虚数特征值(后面讲到,这意味着环状结构)
那么,这个线性系统在不动点附近有着与原非线性系统完全一致的拓扑结构。所以对于 非线性系统的分岔研究,可以在一个局部范围内简化为线性系统的相空间拓扑结构的研究。
我们进一步假设y0=0,这一个非常自然:我们总是可以通过坐标变换,使得y0消失。那么,线性化之后的系统就变成了:
\dot{\bold{y}}=\bold{J}\left( \lambda \right)\bold{y} - (3)
其中 J 是常矩阵。这样我们面对的就是一个最简单线性常微分方程组了。
对于L是微分算子或者其它复杂算子等情况而言,处理起来稍稍有点不同,但是基本思路都是一样的。这里我略过不谈,可以参考非线性算子相关的教科书。
线性常微分方程组的求解是任何一个微分方程课程中必然要讲的基本知识,这里不详细推导。我们直接给出方程(3)的通解如下:
\bold{y}\left( t \right)=\sum_{i}^{}{c_i \bold{X_i}e^{\beta_i t}}
上式中,ci是积分常数,由初始条件可以定解, Xi 是矩阵J的特征向量,对应的βi就是特征值。有了这个通解,我们就可以对不动点附近的相空间结构进行分析了。一般而言,我们面对的是一个N维系统,N可以是任意数。但是,为了理解的方便,我们这里讨论二维的情况,因为它可以很方便地用我们的二维纸面上的图形来表示。对高维系统,就需要发挥想象力,跳出纸面来加以推广了。
对于二维系统,系统由下式表示:
\bold{y}\left( t \right)=c_1 \bold{X_1}e^{\beta_1 t}+c_2 \bold{X_2}e^{\beta_2 t}
我们考虑如下情况:
1、 β1、β1全部为实数,并且β1<β2<0:
此时,系统的相点由两个特征向量的实组合给出。所以任何一个点投影在在这两个向量上的分量就是它们的系数。随着时间的变化,两个向量上的投影都以指数速度压缩,因而向不动点靠拢。特征值绝对值的大小就决定了相应向量上的投影向不动点运动的速度。读者可以自己把这个解对应的相图画出来,这里有几个特点值得一提:
- 由于两个特征向量之间是线性不相关的,所以任意一个位于特征向量轴线上的初始点,必然会沿着特征向量的方向演化,
- 随着时间的增加,任何一个初始点都会向不动点靠拢
- 特征值绝对值的大小决定了向不动点靠拢的快慢。最终,除去沿X2方向演化的轨迹以外,其余轨迹在不动点附近均与X1相切。

我们来讨论稳定性的问题。我们可以看到,对于不动点附近的任何一点,全部演化方向都是向着不动点前进的。所以说,在不动点上的平衡,有任何微小的扰动,系统的演化都会把它“拉”回到不动点上来。我们把它就称为稳定的。事实上,这个不动点在这里有个更炫一点的名字,叫做“ 一致稳定结点 ”。
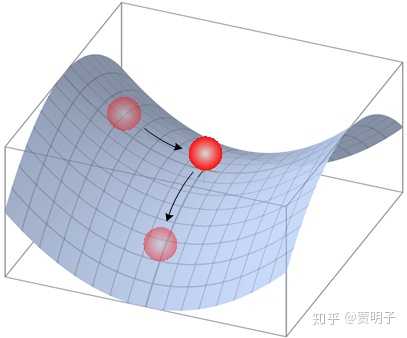
对于这类稳定结点,我们可以用一个坑里的小球来类比。这个不动点就是坑底,任何一个地方的小球都会向这个坑底演化。对于坑底的小球,我们不论如何扰动它,它偏离后总是又回到坑底,这是典型的 稳定平衡。
2、 β1、β1全部为实数,并且β1>β2>0:
这种情况与第一种是一致的,除去一点:即随着时间的增加,所有的点都是离不动点远去的。所以,它的相图的形状与第一种情况完全相同,只是方向相反。
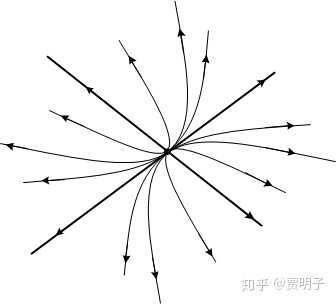
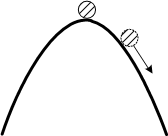
同样地,它的稳定性也会与第一种情况相反。我们看到,除非是完全确定地落在不动点上面,其余任何一个附近的点都会以指数速度远离。也就是说,一个任意小的扰动,使系统从不动点偏离一点点,这个偏差就会以指数速度放大,进而发散。系统的平衡就崩溃了。这个就是不稳定的。同样,这个不动点就被称为“ 不稳定结点 ”。
做一个与前一种情况相似的类比,这个不动点是一个峰,只有恰好落在峰上的小球才可以保持平衡,而其余的任何一点都会向着远离的方向运动。对峰上的小球的无论多小的扰动,都会使小球的平衡瞬间崩溃。这就是一个典型的 不稳定平衡 。
3、 β1、β2全部为实数,并且β1>0>β2:
此时,由于β1>0,意味着相点在X1上的投影是随时间发散的,而β2<0则意味着在X2上的投影是随时间收敛的。所以,相点的运动轨迹必然是从X2方向上靠近不动点,而从X1方向上远离不动点。如下图:
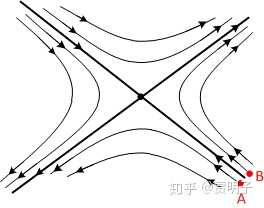
这里,我们可以看到,只有初始点严格位于X2延伸所构成的直线上时,它才会向着不动点演化,并最终达到不动点。而偏离一点,就会使得相点先靠近不动点,但是随后就迅速远离了。所以我们说,这也是一个不稳定的不动点,称作“ 鞍点 ”。
我们注意到,虽然是个线性系统,我们已经开始看到混沌行为的最原始发端了:初始条件敏感性。如图A和B两点分别位于X2的两侧并且任意靠近,但是无论它们之间的距离多小,它们的演化轨迹总是迅速分开的。当然,在这里这种初始条件敏感是非常局部的,并且是可预测的,但是在非线性系统当中,不动点的个数可能是很多的,当然其中鞍点也不少。想象一下系统中有多个鞍点,整个流形就会被搅得乱七八糟,而这种敏感性会迅速扩散,这一点我们在KAM中会很明显看到。
4、 β1、β1为复数a±bi,并且a<0:
虚部意味着震荡。
- 与实数特征值的情况相同,复特征值的实部的绝对值表示了相点向不动点靠拢(或分离)的速度。负数的实部表示相点向不动点靠拢。
- 虚部的存在表示相点的运动存在振动。具体讲,虚部的绝对值决定了相点振动的周期。
那么此时的相图就表现为螺旋线,如图所示
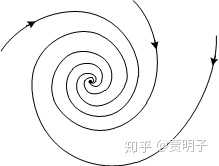
这表示在不动点的附近,所有的点都以螺旋的方式向不动点靠近。与前面道理相同,这是一个稳定的不动点,称作“ 稳定焦点 ”。
5、 β1、β1为复数a±bi,并且a>0:
与上面一种情况相同,此时仍然是螺旋线,但是由于特征值的实部是正数,这就表示任何不动点附近的点都是向着远离不动点的方向演化的,如图所示
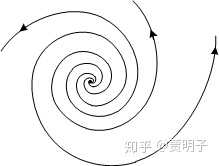
同理,这是一个不稳定的不动点,称作“ 不稳定焦点 ”。
6、 β1、β1为纯虚数,即a=0:
这种情况与前面焦点的结构所不同的是,特征值的实部为零,我们可以很自然地推断,不动点附近的演化既不远离它,也不向它靠拢。通过对通解的分析,确实如此。此时系统表现为周期性振动,周期有b决定,在相图上就是环状结构。
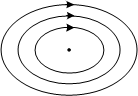
此时,系统表现为以不动点为平衡点的纯周期无阻尼振动,这个不动点被称为“ 中心 ”。这里值得注意的是,它的结构其实与原来的非线性系统未必同胚。这个在Hopf分岔中我们会讨论。
好了,我们已经知道了,一个非线性系统在围绕不动点附近的局部拓扑结构可以完全通过线性化后的简单系统来分析。从上面的讨论我们可以看出,这个不动点的性质完全由线性系统的特征值确定。我们这里总结如下:
- 所有特征值的实部全部为负数:这是一个稳定不动点,包括稳定结点和稳定焦点两种情况。
- 至少有一个特征值实部为正数:这是一个不稳定不动点,包括不稳定结点、不稳定焦点、以及鞍点三种情况。
- 纯虚数特征值:系统表现为周期振动,这是一个中心不动点。
另外,需要指出的是,上面除去最后一种情况,其余的不动点都是具有实部不为零的特征值的,这些统称“双曲不动点”(hyperbolic equilibrium)。这个名字有些误导 - 它并非指不动点具有双曲结构,像鞍点。但是由于种种原因,这个不太确切的称呼被沿用下来,并成为标准。虽然我们讨论了纯虚数的情况,但是这种情况,正如前面所指出的,并不与非线性系统保持相同的拓扑结构。但是它确实是与环状结构的诞生相联系的。这种在相空间中但是环形结构的,叫做 Hopf分岔 。
一般而言,相空间中的特殊结构基本上就是以上所述的几种类型。但是在高维情况下,一种非常常见,并且非常重要的结构 – 环面 – 这里没有讨论,这种结构对于系统进入混沌至关重要。
这里所提到的都是所谓“局部结构”,当我们放眼全局,会有一些不一样的结构出现。例如,当一个鞍点A与一个中心不动点B环相遇的时候,我们会看到这样两个局部结构合并到一起成为同宿点分岔:
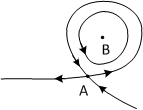
再比如,一个不稳定的焦点,它只是局部发散,在很多时候,周围的流会很快收敛到一个环绕它的环上面去,如:
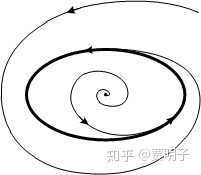
关于环和环面,是走向混沌至关重要的结构,后面我们会看到。
三、何时分岔?
如果你足够细心,你应该已经注意到,我们讨论线性化系统的各种情况,唯独有一种没有去碰,就是有一个特征值为零的时候。此时,我们知道, J 已经不是一个满秩矩阵了。从初等线代的知识我们立刻就可以得到,这意味着一阶线性化不再有效,我们必须从非线性的角度来分析这个问题。具体讲,线性化系统不再与原系统具有相同的拓扑结构。
如果我们回忆微分方程解的存在与唯一性定理,我们很容易得出结论,在雅克比矩阵奇异的情况下,它不满足Lipschitz条件,也就是说,解的唯一性不再有保证。
那么,雅克比矩阵奇异意味着什么呢?我先给出结论:这意味着此时我们到了一个潜在的分岔点。
这个结论的基础就是 隐函数定理(实在是懒得敲公式了,请自行搜索该定理) :
那么,考虑方程(2):
\bold{L}\left( \lambda \right)\bold{y_0}=0
定义了系统的某一个不动点 y0 。我们通过判断它的雅克比矩阵是否奇异,就可以得知这个点是否是一个分岔点。用不太严格的话简单说,就是,隐函数定理告诉我们,在一个不动点附近,如果雅克比矩阵非奇异,则 L 存在唯一的反函数(反算子),知道了这个反算子,我们就可以显式地知道它只有唯一的一个 y0 。进一步简化这个说法,就是:
如果在不动点附近雅克比矩阵非奇异,则不动点唯一。
请注意,前面的定理只是众多版本中的一个特例:我们处理的是实数域中的多元函数,并且参数的维度为1。这个定理存在推广版:对于Banach空间中的非线性映射,并且参数为多维,也有类似的定理存在。为了简化,我在此略过,但是不代表它不重要。事实上,绝大数情况下,我们处理的不是简单的函数,而是包含边界条件的微分算子。
好了,现在我们提出了 系统的一个分岔点的判断依据:雅克比矩阵是否奇异 。如果是非奇异的,那么我们可以保证在这一点附近只有一个不动点。如果雅克比矩阵为零,那么,我们知道这个不动点附近还可能存在其他的不动点 – 系统定态解的个数增加了 – 这就是分岔。
那么现在的问题有点类似先有鸡还是先有蛋了:我们必须要找出不动点附近的奇异性,来判断是否有唯一的不动点,而在这之前,我们必须要在不知道是否存在唯一解的情况下发现这个不动点!要解决这个矛盾通常的做法就是“追踪”。
通过一定的数学处理(具体处理办法可参见Seydel 的 《From Equilibrium To Chaos – Practical Bifurcation and Stability Analysis》),我们能够找出所有的分支。
现在我们有了研究分岔的基本工具,已经可以开始分析一个系统的分岔行为了。具体而言,就是要沿着参数变化的方向, 找到系统中特殊结构何时产生,在一定的参数取值下,这些结构数目的多少,以及它们每个的稳定性。 但是,在这之前,我应该说,我们在寻找分岔的追踪过程中,所关心的并非只是它的奇异性,还有很多其他信息非常有用。请回忆在线性化的讨论中,不同的特征值对应于不同的结构。我们总结的规律就是,特征值的实部相当重要。当它变号(也就是说,跨过零点)的时候,系统的稳定性就会发生变化,并且还可能出现环状结构。并且我们可以注意到,隐函数定理所指出的奇异点的出现,也正是特征值实部跨越零点的一个特殊情况(出现一个零特征值)。所以,我们可以很放心地下一个断言:
雅克比矩阵特征值实部的变化,决定了相空间中特殊结构的个数以及它们每一个的性质。
四、静态分岔
我们现在开始讨论系统的分岔行为。前面提到分岔追踪的大致过程,这里在稍微展开一点。分岔分析的意义在于,它可以以一种非常明确的方式让我们看到,当一个系统从简单到复杂演化的时候,系统的复杂性是以一种什么样的机制产生,并且帮我们确定,系统在什么范围内是“简单”的,什么范围内是“复杂”的。而这种复杂性的表现又是怎么样的,我们如何从这个复杂系统中提取出一定的规律。
这里特别提醒,我们所说的系统由简单向复杂“演化”,与动力学系统随时间的演化并不是一个概念。为了小心翼翼地区分开来,我把前者叫做“参数演化”,后者叫做“时间演化”。
参数演化指的是系统相空间的拓扑结构随着控制参数的变化而变化 ,也就是说,非线性算子 L 的性质随着参数λ的变化。例如,在三体系统中,我们可以针对其中的两个主要物体作为研究对象,建立数学模型,而把第三个作为一个对这个数学模型的修正。这样一来,第三个物体的质量就是整个系统的一个参数。三体问题是一个很棘手的问题,但是我们可以通过控制这个参数来由简入难地来处理这个问题:首先,我们令第三体的质量为零,那么,我们就得到了一个二体问题,这是个非常明确的可积系统。然后,我们渐渐增加这个质量,来观察系统的结构随着质量的变化会发生什么样的行为。如前所述,这是一个分岔的研究过程。分岔图上的每一个点,对应于一个确定系统的相图的全部结构。 参数演化的过程就是相图的变形过程。如果相图的变形不导致拓扑结构的变化,那么即使变形再巨大(从茶杯变成面包圈),也没有分岔的发生。反之,如果是一个微小的形变,但是导致了拓扑结构的变化,此时就有了分岔。
而 时间演化指的是,对于一个参数已经确定的系统,它从一个初始点随时间的变化 。
如果说参数演化研究的是不同参数下的整个相图的变化,那么时间演化研究的是一个确定参数下的一个确定的相图中对应于不同初始点的轨迹变化。
而分岔分析,我们所研究的正是参数演化。
前面我们对分岔给出了定义,就是系统相空间随着参数的变化而产生的拓扑结构的变化。我们还总结出来拓扑结构变化的判据,就是雅克比矩阵特征值实部跨越零点。但是,系统无论是跨越奇异点,还是特征值跨越纯虚数轴,它们在这个分岔点上面还有更加精细的性质。伴随着这些精细性质的不同,它们的分岔行为也表现不同。我们可以把前面的那些典型拓扑结构以及它们之间的变化当成套路,来套这个分岔过程,就有了一个概念叫做 “标准型” :
简言之,标准型的概念就是一个与我们所关心的系统具有完全相同分岔行为的最简系统。
例如,一个最简单的标准型叫做 鞍点-结点分岔 (saddle node bifurcation),又称作fold分岔, 它具有如下标准型:
\dot{y}=y^2 \pm \lambda
为了直观,我们在二维(y-λ)图中表示这个这个局部分岔,如下图。当然,这是一个N+1维的系统,但是我们总能选取一个y相关的数值来代替N维的y,例如y的一个分量,或者是y的一个范数。在本文中,不再区分它与y的不同。
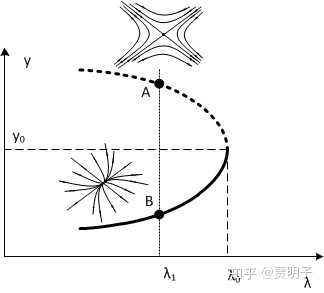
以上产生这个分岔的条件里很明确地表明,这是一个实数特征值跨越零点时的行为,并且不存在二阶奇异性,也不存在对参数偏导的奇异性。如图所示,当λ<λ0 时,系统存在两个不动点A和B,其中A在相图中表现为一个鞍点,而B表现为一个结点。而λ>λ0 时,系统不存在不动点。这里我才用了分岔图中的一个常规:稳定的分支用实线表示,而不稳定的分支用虚线表示。虚线部分的每一个点都是鞍点,而实线部分对应的是稳定结点。在上图中对于每一个小于λ0的系统,相图中都同时存在一个鞍点和一个结点。这个系统在相空间中结构随着参数的变化可以大致表现如下:
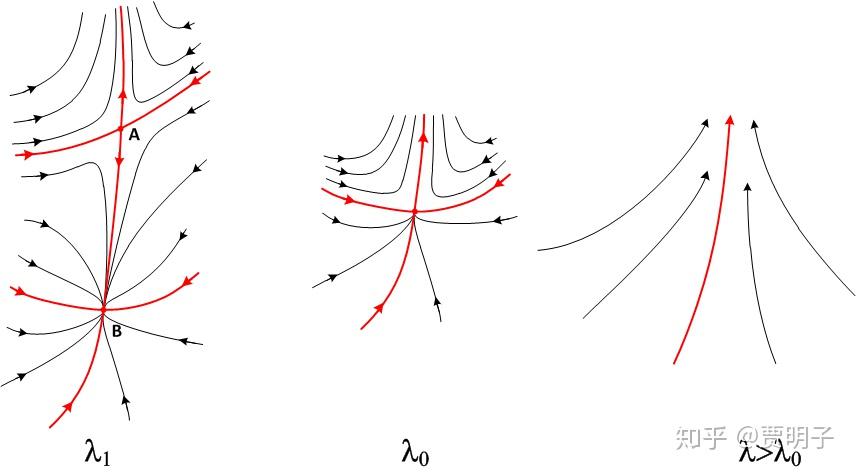
当λ<λ0 时,相图中存在一个鞍点A和一个结点B,随着参数的演化,A点和B点互相靠近,当λ=λ0 时,AB两点重合,系统就只有一个不动点。此时参数再增大,则系统中就没有不动点存在了。
这个分岔在非线性系统中几乎是最为普遍的一种,以至于频频出现于各个领域当中,而不同领域的人对它有各种不同的称谓。一个比较常见的管它叫做 “折点”(turning point) ,以与分岔点区分。因为此时系统虽然有不动点个数的变化,以及稳定性的变化,但是并没有两个分支交叉的行为。
这个分岔图从几何上看,有一个很明显的特征,就是它很容易通过坐标变化“旋转”90度,从而使得这个折点不再奇异。这在数值分析过程中非常有用,也是它与其它类型的分岔明显不同的地方。
类似的,其它的类型奇异点,由于它们高阶、参数偏导等精细奇异性的不同,还会有很多不同的表现行为,这里只列举出这些类型的形式,不再一一讨论。有兴趣的人可以参考相关非线性分析的书籍。
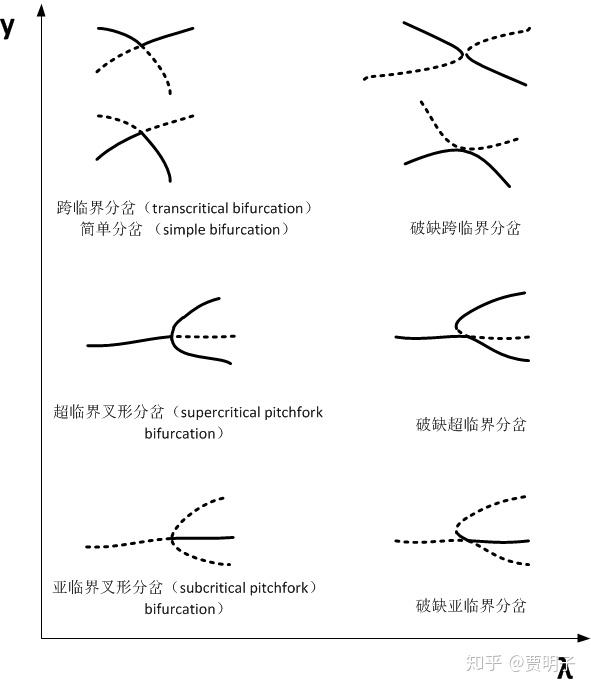
到此为止,我们所谈到的分岔类型都有一个共同点:它都是 在不动点之间的变化 ,这样的分岔往往被称作“ 静态分岔 ”或“ 稳态分岔 ”。我们说,在一个动力学系统中,静态分岔是缺乏“生命”的。因为在这类分岔当中,一切运动最终收敛于静态:没有运动,没有振荡,没有化学反应,也没有生物现象。在系统的参数演化过程中,它不会带来让人为之一振的现象,简单系统不会向复杂系统变化,因为参数的变化只会给我们带来不同位置静态,但我们也仅仅限于静态而已。
五、Hopf分岔
我们来讨论一下另外一类分岔,首先,我们知道,前面讨论的静态分岔的产生的原因都是因为特征值跨越零点,但是,我们还知道,特征值为复数的时候,它的实部跨越零点也会产生分岔,这就是Hopf分岔。如下图所示,特征值如果从实轴上跨越虚轴(零点),那么这就是个静态分岔,如果从其他地方跨越虚轴,那么这就是个Hopf分岔:
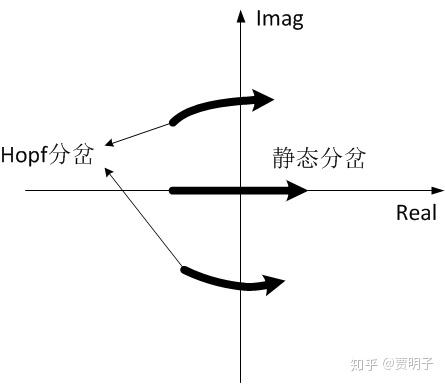
Hopf分岔从物理上讲,就是周期振动从静态中产生,而从几何上讲,Hopf分岔就意味着相空间中一个点变成环状结构的过程。它是动力学系统中复杂性的真正体现,因为它会涉及到系统由静态自发产生运动的过程。与前面不动点的情况最大的区别就是:它产生周期性运动,而不是静态解。这对混沌而言至关重要,一个静态的系统不可能是混沌系统。当然,简单周期运动的系统也不是混沌系统,但是后面我们会看到,在周期运动稳定性丧失的情况下,连续的分岔使得系统的特征谱不断产生新的谱线,直至最后变为连续谱,而运动的周期性也丧失了,变成了“无规运动”。
下面详细定义Hopf分岔:
(算了,不详细定义了,公式太多。)
此分岔点具有如下标准型:
\dot{y}=\left( \lambda+i\beta \right)y+l\left( y_0,\lambda_0 \right)y\left| y \right|^2
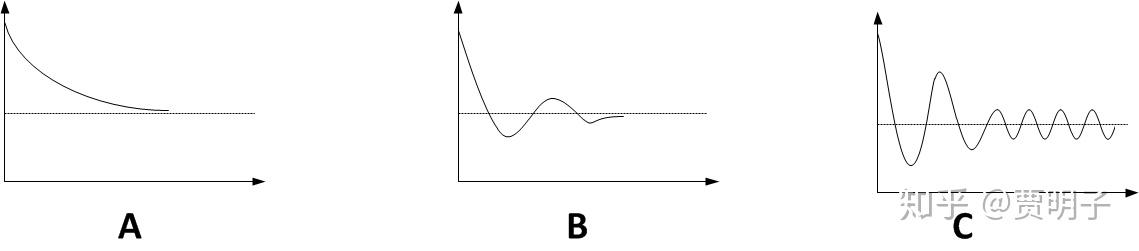
这个分岔过程可以简单地用下图表示,我们可以看到随着参数的变化,环形结构是如何出现的。系统的维度有y1和y2组成,当参数λ小于分岔点的时候,这时系统呈现一个不动点,这个不动点是一个稳定焦点。当参数跨越分岔点时,一个极限环产生了,它围绕着这个不动点。极限环外面的流不再收敛到不动点上,而是收敛到这个环上面。同时,这个不动点变成了不稳定焦点,从这个不稳定焦点发散的流也收敛在极限环上面。此时极限环为稳定的。
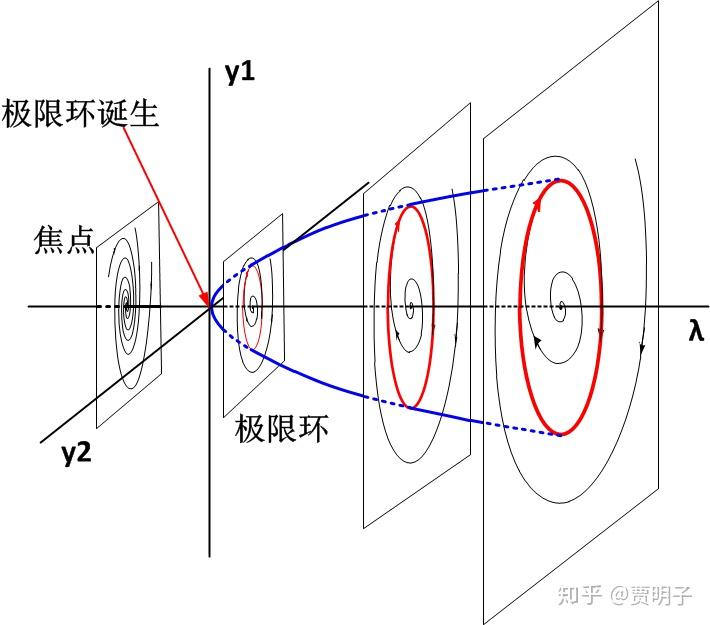
上式中有一个参数, l ,被称作第一李雅普诺夫值,L的值可以从f中计算出来,它非常重要,它的符号决定了这个极限环运动是否稳定,如下图所示。它的计算这里略过不提,有兴趣的读者可以参考进一步的资料。
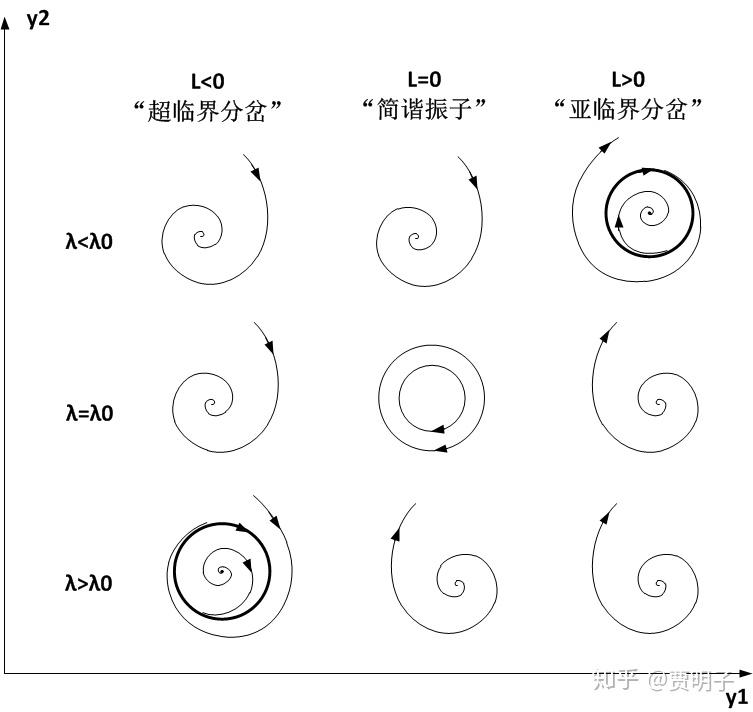
值得注意的是,在绝大多数情况下,在跨过Hopf分岔点的时候,不动点的性质并没有发生变化,仅仅是稳定性变化了而已。这与纯虚数特征值的线性化系统不同,因为线性化系统中不动点表现为一个中心,而非线性系统中它一直是个焦点。正如前面我所提到的,在纯虚数特征值的情况下,线性化系统与非线性系统不再具有同胚的性质。
六、走向混沌的岔路
那么,对于环形结构,仍然有很多非常复杂的分岔行为。例如说,一个环面分岔:
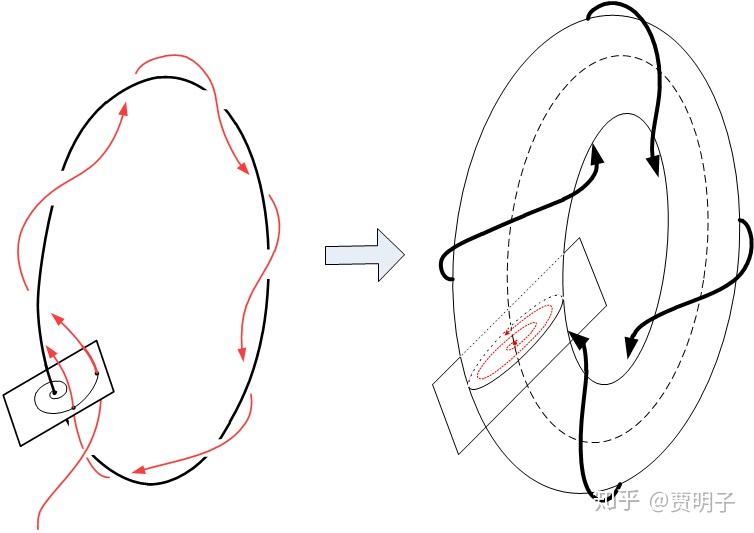
这种分岔,就是系统从以一个极限环的方式震动,变为一个环面震动的过程。这出现在大于三维的系统中。我们可以想象在更高维系统中会有更加复杂的变化。
熟悉三体问题的人可能都很清楚,环面分岔这个东东,在三体问题中的重要性。但是我这里想说一个比较简单的过程: 周期倍化(period doubling) 。
比如说下图中,红色的环是一个稳定的极限环结构。黑色的螺旋线表示某个演化轨迹。我们可以在环上面“截取”一个切面,显示轨迹每次穿过这个面所产生的离散点的变化过程。这个面叫做“庞加莱面”,而由轨迹产生交点的过程叫做“庞加莱映射”。
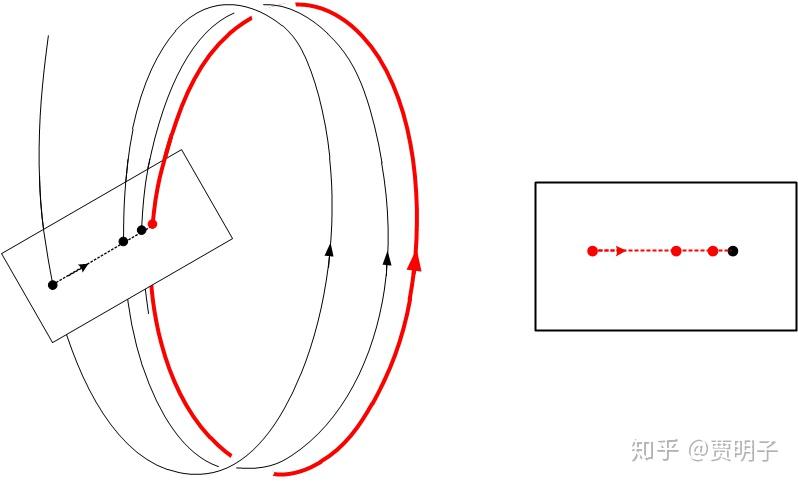
在系统参数发生变化时(具体不详解),这个环会突然发生“倍化”,也就是“绕两圈”的变化:
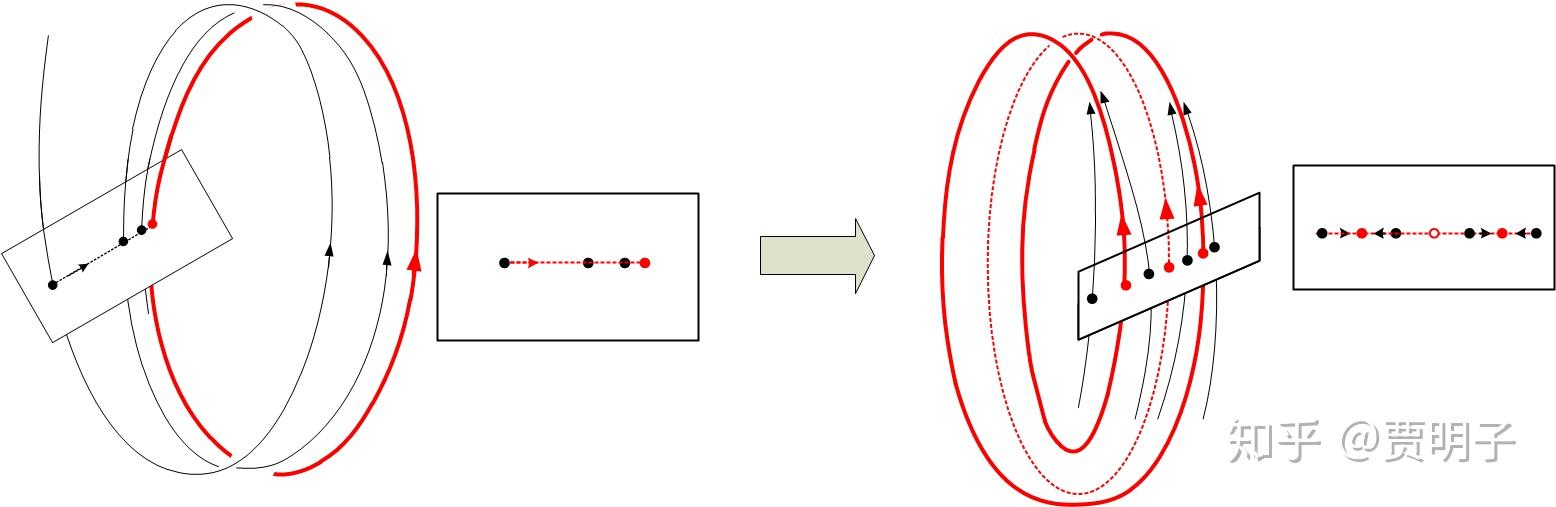
原来的那个环突变为不稳定环,而新产生的这个“绕两圈”的环是稳定环。于是原来收敛于“单环”的轨道就会向着新的“双环”靠拢。
随着参数的不断变化,这种“倍化”现象会不断出现,于是从“绕两圈”变为“绕四圈”再变为“绕八圈”等等。比如说,下图是一个所谓的“ rossler吸引子 ”随着某参数的倍化过程(图形来自维基百科,rossler attractor词条):
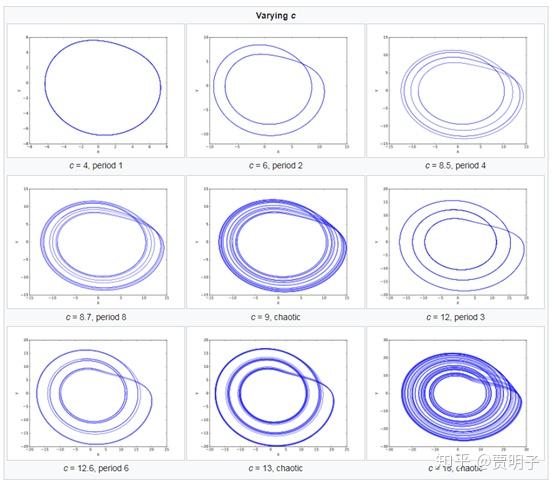
我们可以看到这个不断倍化过程,直至最后成为类似这样:
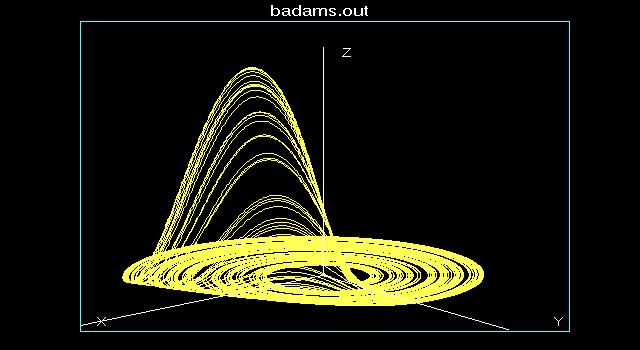
这个倍化的过程将会变化很快,参数每增加一个δ,它就如是“倍化”一次,每倍化一次,它的频谱中就多一条谱线。于是乎它的频谱越来越宽,并且每次δ的间隔会越来越小。直至突破某一点后,它的频谱组成如此之复杂,已经不再是震荡了,而是一个无规律的运动。
这种周期倍化的过程,最经典的就是所谓的“ logistic map ”,我们可以看到这种一分二、二分四的快速倍化过程,以及每次倍化之间的间隔越来越小(图片来自维基百科):
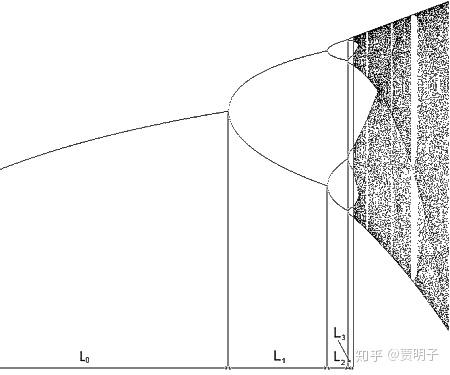
事实上,每两次倍化之间的间隔,按照一个等比的常数缩减,这个常数叫做 Feigenbaum常数 。这个常数数值是 4.669201609102990671853203821578… 。
我们由此可以看到,在一定的参数区域中,这个吸引子的周期已经被倍化无数次了,以至于空间中“ 稠密 ”地布满了各种不稳定的轨道。这里稠密的意思是, 在任意一个不稳定轨道附近任意短的距离内,我们都可以发现另一个不稳定轨道 。
这意味着什么呢?我们从简单的二倍周期来说明一下。当一个环被二倍化后,它原来的环就成为不稳定的轨道,那么它附近的轨道必然就向二倍轨道收敛。一个初始的粗粒随着时间的演化就会是这样的:
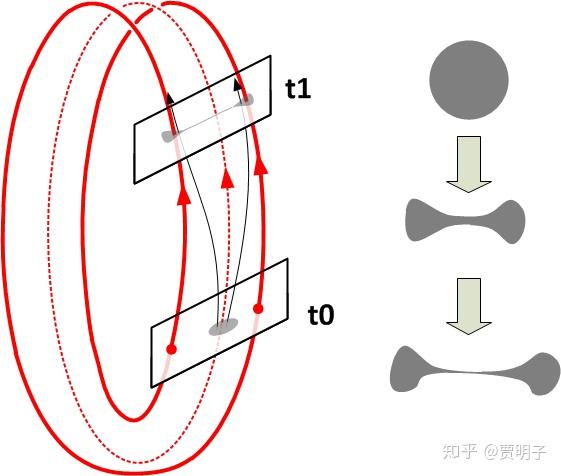
它们会很快地扩散成为两团。当空间中密布着这样的不稳定轨道时,这种扩散就会迅速地遍布空间。如下图(这个图和上面那个动图都出自一个很酷的网站, http:// blc.arizona.edu/courses /schaffer/demos/rossler/rossler2.html ),一个非常小的黄色的初始粗粒(意味着很确定),最终随时间演化过程中会发生如下变化:


这就意味着,初始的粗粒迅速扩散至整个空间,也就是确定性的丧失。这就是混沌的随机性的来源 – 轨道还是确定的轨道,但是我们没有办法确定地跟踪它了,因为轨道太“密”了。它们无线细密地编织在一起形成了一个“轨迹带”:

请参考
七、条条大道通混沌
前面所说的只是最简单易懂,且最为大众所知的混沌机理,其实还有很多种通往混沌之路。除了前面说的 周期倍化 之外,还有 环面分岔路线 、 中间路线、同宿流形纠缠 等等一系列。这里就不多讲了。
谢邀。
既然题主注明“越通俗越好”,那就尽量不整那些复杂的数学定义和公式来解释问题。 主要介绍 俩理论的研究对象(为什么要研究它们?它们是什么?)而 略过 具体研究方法(如何研究?科研界前沿结果有哪些?)。
先上俩直观的关于混沌与分岔的图,下文详细解释:
1. 【假设您已学过,温故知新】Nonlinear dynamic systems(非线性动态系统)
致虚极,守静笃,万物并作,吾以观复。 ——《老子 \bullet 道德经》
系统理论研究的是事物发展变化规律的学问。设一个系统的变化规律可以用常微分方程表示为:
\dot{x}=f(x(t),u(t),r(t))
其中:
x(t)\in\mathbb{R}^n 表示系统 状态量 (描述系统目前情况的向量 i.e.充要地描述了系统目前的状态。为一切系统经历历史的总和 i.e.推测系统未来的变化只需要当前的 x 而不需要知其历史经历。)。
u(t)\in\mathbb{R}^m 表示外界(人为)对系统的 输入 。所谓系统 控制 ,控制的便是它。
r(t)\in\mathbb{R}^p 表示系统的 待定参数 ,它可以是随时间变化的(“非常道”),也可以为常数(一旦设计好系统,开始运行后就不变化了)。
- 如果一个系统是 线性 的( f 关于 x,u 线性),那么可以表示为:
\dot{x}=A(t)x(t)+B(t)u(t) 其中 A(t),B(t) 隐含了 r(t)
- 如果系统不仅线性而且不随时间变化(LTI,Linear Time Invariant),那么
\dot{x}=Ax(t)+Bu(t) ,我们可以方便地(数学上严格证明地)研究它的稳定性、可靠性、鲁棒性、可控性……
那么问题来了 :如果 f 不是关于 x,u 的线性函数怎么办?那么就涉及到非线性控制理论。主要研究的便有 混沌 和 分岔 。
2.Chaotic behaviour(混沌)
差之毫厘,谬以千里。 《朱熹 \bullet 论语集注》
对于一般的 非线性 系统 \dot{x}=f(x(t),u(t),r(t)) 来说,为了专注于研究对象,咱们先不考虑外界的控制量 u ,只考虑后两者 \dot{x}=f(x(t),r(t)) 。甚至认为它不随时间变化 \dot{x}=f(x(t),r) 。
那么问题来了 : x 的 初始值 x(t=0) 的改变会对这个系统未来的发展产生多大变化?
对应的没有控制量 u 的 线性系统 \dot{x}=Ax(t) 中,可以证明: ||x_1(t=\tau)-x_2(t=\tau)||\leq||x_1(t=0)-x_2(t=0)||e^{\lambda^{A}_{max}\tau} ,其中 \lambda^{A}_{max} 是 A 特征值中实数部分最大值。通俗的说, 系统状态起始点的差距 ,在经过时间 \tau 后,会发展成一个 有上限 e^{\lambda^{A}_{max}\tau} 的最大变化。
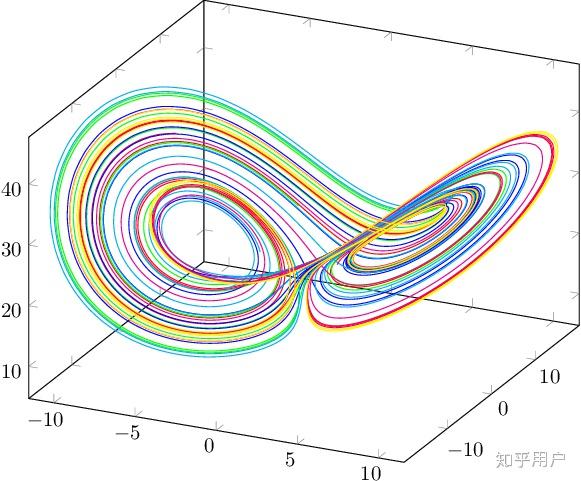
而 非线性系统 中就不然了。请看 蝴蝶效应 :

上图为 非线性系统洛仑兹吸引子 \begin{align*} \dot{x} &= \sigma(y-x) \\ \dot{y} &= x(\rho-z)-y \\ \dot{z} &= xy-\beta z \end{align*} (三维)状态量随时间运动图。每条颜色的线为不同初始值发展成的运动路线。大家可以看到,在 原点附近,差一点点初始值,其发展变化会迥然不同 。这种效应便是 混沌 。因为这张图形状如蝴蝶,且爱德华 洛仑兹本人(气象学家,洛仑兹吸引子以其命名)用 “一只蝴蝶在巴西轻拍翅膀,可以导致一个月后德克萨斯州的一场龙卷风。” 来形容这种效应,所以大家也用 蝴蝶效应 来表达“差之毫厘,谬以千里”的混沌。 线性系统 则不然, 微小的初始点变化在微小的发展时间段内必然造成微小的差距 。
这种看似无序(混沌)的运动是非线性系统区别于线性系统的主要特征,又比如 双摆 的运动轨迹:



3.Bifurcation(分岔)
①量变是质变的必要准备,质变是量变的必然结果。
②质变不仅可以完成量变,而且为新的量变开辟道路。
③总的量变中有部分质变,质变中有量变的特征。
——《黑格尔 \bullet 辩证法》
咱们说完了差之毫厘,谬以千里,再来说说 量变到质变 。这次咱们的研究对象不是系统状态随时间的变化,而是 系统参数 r 对系统的影响。老规矩,先考虑最简单的 没有外界控制量输入的 , 参数在状态发展中不变 的非线性系统 \dot{x}=f(x(t),r) 。
我们来研究 平衡点 \dot{x}=f(x,r)=0 (即随时间不发生变化的起始点) 随参数 r 的变化情况 。
- 例子1 (Pitchfork bifurcation) \dot{x}=rx-x^3
易求得: r<0 时,只有一个稳定平衡点 x=0 ;当 r>0 时有一个不稳定平衡点 x=0 和俩稳定平衡点 x=\pm\sqrt{r} ,上述结论可以用下图表示:
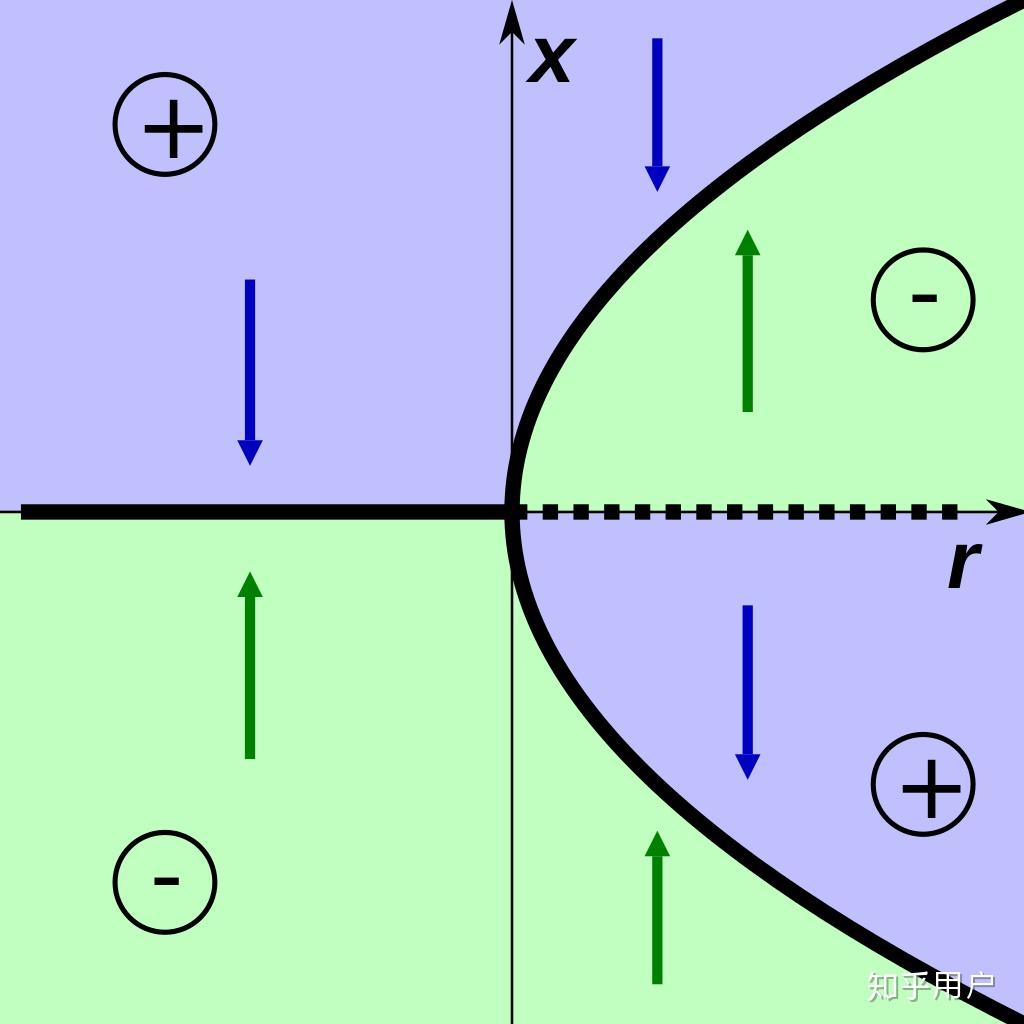
实线为稳定平衡点,虚线为非稳定平衡点。可以清晰地看到平衡点的分布在 r=0 处分岔。
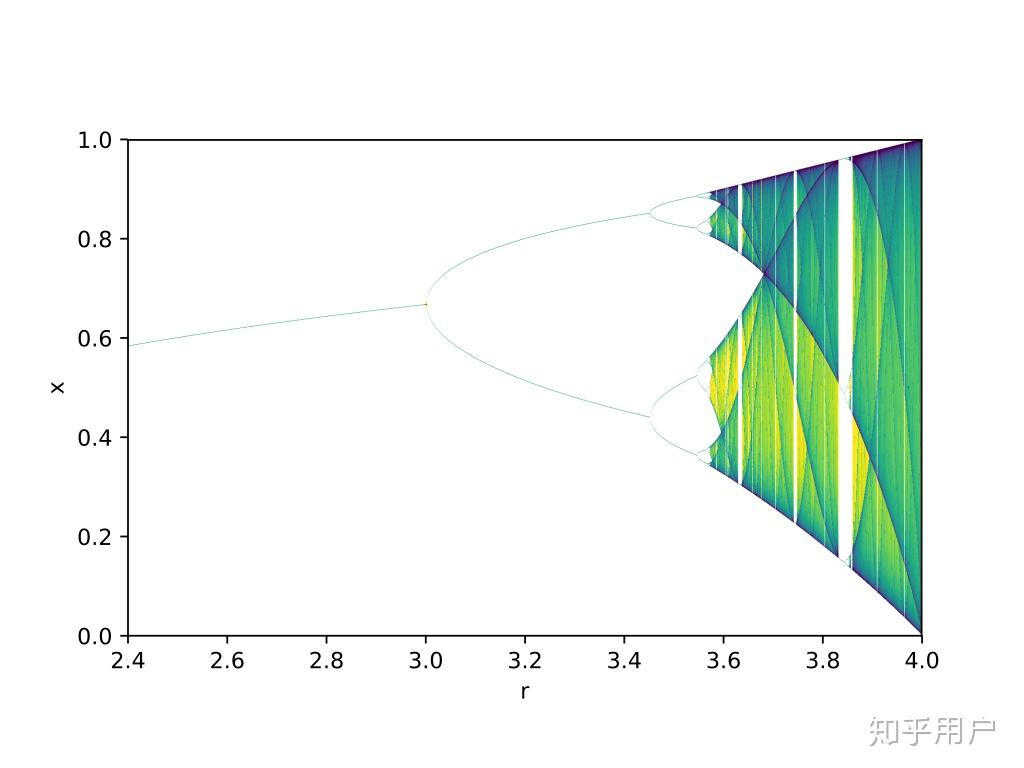
- 例子2(Logistic map) x_{n+1}=rx_n(1-x_n)
这是个离散的动态系统,不妨碍它的变化随着参数而发生量变到质变的积累。下图是平衡点分布:
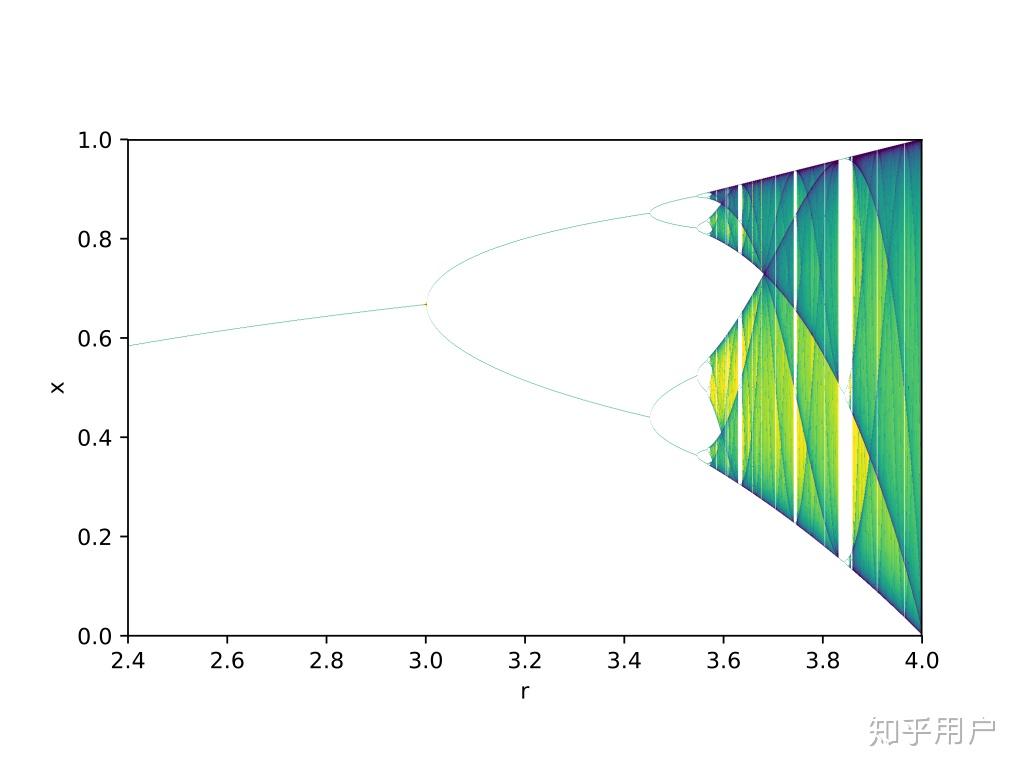
可以看到系统 平衡点 随参数 r 的变化发生了明显的分岔变化。
4.小结
- 分岔与混沌针对的是 非线性系统 。
- 混沌 表达了非线性系统 初始状态量 的“差之毫厘谬以千里”,即 系统初始状态的微小差别 会导致 迥然不同的状态发展变化 。例:人类文明的发展变化是混沌的,不同的初始资源点会发展成迥然不同的文明形态。
- 分岔 表达了非线性系统 参数 量对 平衡点的量变到质变的影响 。例:公共政策的变化会引来经济体发展平衡点的分岔,由单一的经济发展趋势变为复杂的发展趋势。
更多我的相关回答请参阅:
- 近千赞的线性代数打通任督二脉的综述:
- 留学生活拾贝: