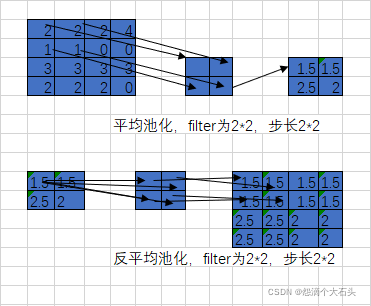
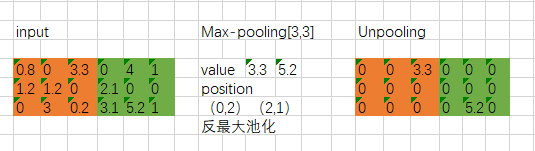
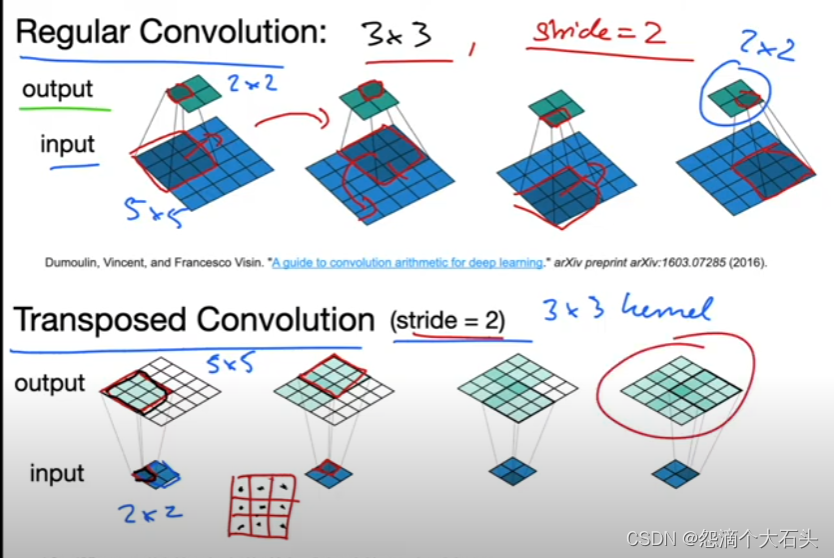
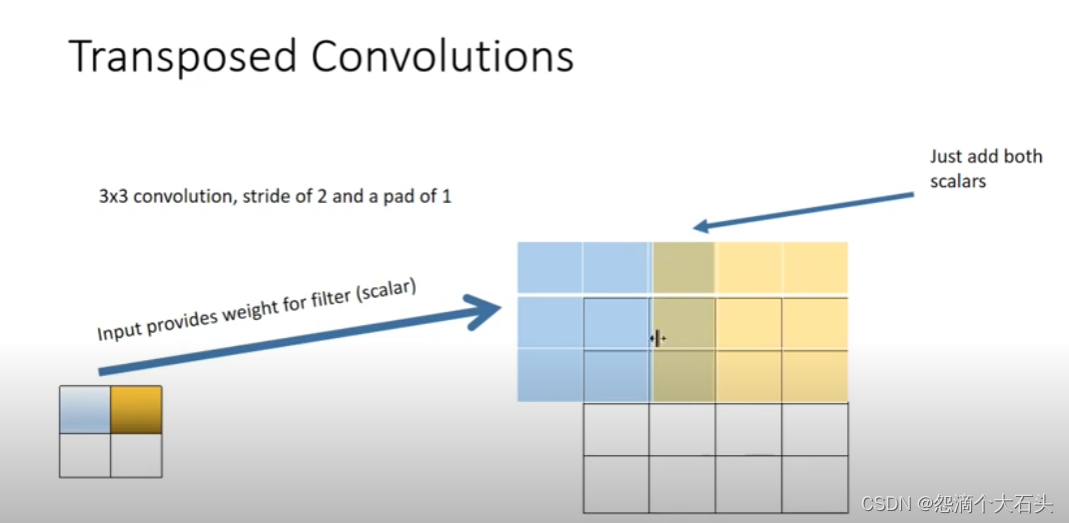
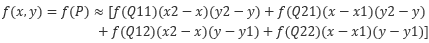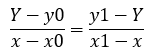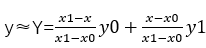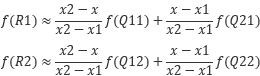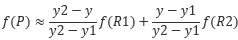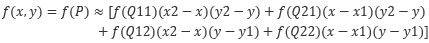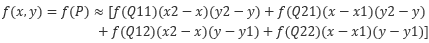一般图像分割的时候,需要对图像进行像素级别的分类,因此在卷积提取到抽象特征后需要通过上采样将feature map还原到原图大小,在FCN和U-net等网络中都提到了上采样的操作,这里会一些上采样的方法进行总结。
最简单的图像缩放算法就是最近邻插值,也称作零阶插值,就是令变换后像素的灰度值等于距它最近的输入像素的灰度值。算法优点在与简单、速度快。
先假设一个2X2像素的图片采用最近邻插值法需要放大到4X4像素的图片,下图左边为原图,右边为要缩放的图片,我们首先将缩放完成的图片生成一个空白图,然后在依次向其填值。
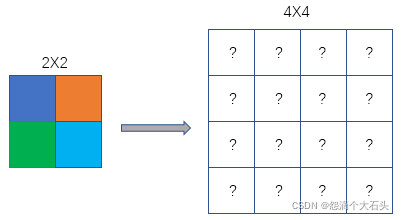
那么右边的?号需要填充的值用到了下面的公式:
srcX = dstX
(srcWidth/dstWidth)
*
srcY = dstY
(srcHeight/dstHeight)
*
scrX、scrY:目标图像(也就是上图右边的图像)某个点的横纵坐标
srcWidth:原图像(也就是上图左边的图像)的宽度
srcHeight:原图像(也就是上图左边的图像)的高度
dstWidth:目标图像(也就是上图左边的图像)的宽度
dstHeight:目标图像(也就是上图左边的图像)的高度
我们一般是以左上角的那个像素点坐标为(1,1),即如下图的x-y坐标系,一个像素点的大小为1
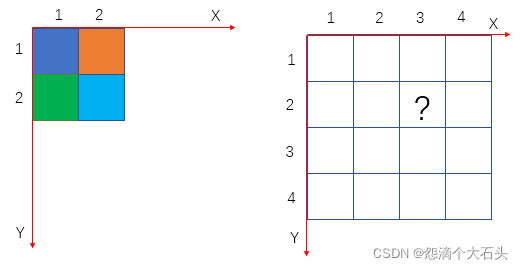
上图右边?号的值为:
srcX=3*(2/4)=1.5,
srcY=2*(2/4)=1;
故?处的像素应该为原图像中的(1.5,1)像素的值,但是像素坐标没有小数,一般采用四舍五入取最邻,所以最终的结果为(2,1),对应原图像的橙色。
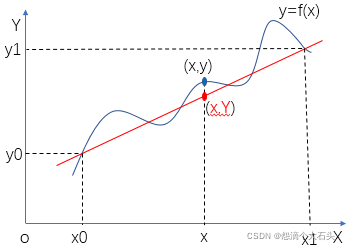
在讲双线性插值法之前先讲一下线性插值,线性插值就像我们平常说的线性关系。如图所示现在已知y=f(x)的两个点坐标分别是(x0,y0),(x1,y1),现在在区间(x0,x1)内给定任意x,如何求y,线性插值法采用图中红点的y值代替f(x)的y值。其实也就是把(x0,y0),(x1,y1),两点看成一条直线,我们认为我们要求的点在这条直线上。 假设x处的直线上的红点坐标为(x,Y),那么Y约等于y。也就是(x0,y0)到(x,Y)和(x,Y)到(x1,y1)的斜率一样,根据图可以得到公式:
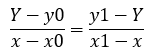
一般转换为非隐函数可以近似为
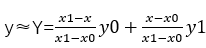
现在我们就可以讲双线性插值法了
双线性插值法也叫双线性内插,根据前面讲的就很容易想到是在两个方向分别进行一次线性插值 。
如坐标图所示,用横纵坐标代表图像像素的位置,f(x,y)代表该像素点(x,y)的彩色值或灰度值
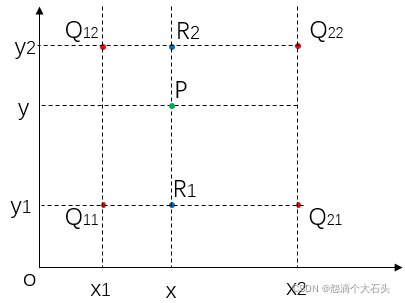
现在假设目标图像的像素点(x’,y’)映射到原图像中是(x,y),也就是图中的P点。设Q11 = (x1, y1)、Q12 = (x1, y2)、Q21 = (x2, y1) 、 Q22 = (x2, y2),图中Q11,Q12,Q21,Q22分别为距离P点的最近的四个点。分别在X方向进行两次插值,最后在y方向进行插值即可得到目标图像的像素值。公式如下:
先计算X方向(也可以先计算Y方向,再计算X方向)的线性插值:
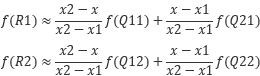
再在y方向进行线性插值得到f§:
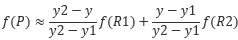
经过公式的进一步化简可以得到:
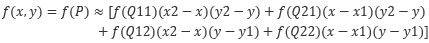
由于是最近的点,所以Q的四个点的坐标之间相差1,故进一步化简为: