图像算法在数值计算中的应用(1):Canny边缘检测算法
引言
有限差分方法 (FDM)是计算机数值模拟最早采用的方法,至今仍在广泛应用。该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。在直角坐标系下,求解域差分网格通常为均匀的矩形,在表达非矩形物体边界时通常需要采用坐标映射或者网格点逼近,而网格点逼近较为简单快捷。
我们对有解析式的几何边界,构造有形状信息的布尔矩阵,可以实现边界形状的识别 Python数值优化:使用Euler法求解二维热传导方程2 。对于一般的图形通常没有解析边界,使有限差分方法适用于一般(平面)几何的关键是要有一个“形状”矩阵,其值表示域的外部,内部和边界。而图像就是用矩阵存储的,包含许多成熟的特征识别算法,因此考虑采用图像的方法来处理,主要利用的就是边缘检测算法。
Canny边缘检测算法 由计算机科学家 John F. Canny 于 1986 年提出,主要可以分为以下几个步骤
- 图像灰度化(降维处理)
- 高斯滤波(平滑和降噪)
- 计算图像梯度值和方向
- 应用非极大值抑制NMS
- 双阈值检测确定边界
灰度化
灰度化实际上是一种降维的操作,将三个通道的像素值转换为单通道数据,减少计算量(如不进行灰度化,也可以直接进行后面步骤),后面针对单通道进行计算。
def img_grey(img):
Grey(i,j) = 0.3 * R(i,j) + 0.59 * G(i,j) + 0.11 * B(i,j)
img_grey = np.dot(img[...,:3], [30, 59, 11])/100
return img_grey
高斯滤波
高斯滤波主要使图像变得平滑,减少噪声,但同时也有可能增大了边缘的宽度。其作用原理和均值滤波器类似,都是取滤波器窗口内的像素的均值作为输出,而其系数按照高斯函数离散化,具体如下:
H_{i,j}=\frac{1}{2\pi\sigma^2}exp(-\frac{(i-k)^2+(j-k)^2}{2\sigma^2})\\
滤波核大小为(2k+1, 2k+1), 这里 i 和 j 从0开始计数,与Python编程时保持下标一致,而MATLAB从1开始计数
\left[ \matrix{ H_{0,0}&H_{0,1}&H_{0,2}\\ H_{1,0}&H_{k,k}&H_{1,2}\\ H_{2,0}&H_{2,1}&H_{2,2}\\ } \right]_{3\times3}\\
def gaussian_kernel(sigma,size):
Create a (2r+1)x(2r+1) gaussian_kernel
H[i, j] = (1/(2*pi*sigma**2))*exp(-1/2*sigma**2((i-r-1)**2 + (j-r-1)**2))
Parameters
===========
sigma: Standard deviation
size: Kernel width size
r = int(size/2)
kernel = np.zeros((size,size))
k_sum = 0
for i in range(size):
for j in range(size):
kernel[i, j] = np.exp((-1/(2*sigma**2)*(np.square(i-r) + np.square(j-r))))/(2*np.pi*sigma**2)
k_sum = k_sum + kernel[i, j]
# Normalized the kernel
kernel = kernel / k_sum
return kernel
构造一个3x3的kernel窗口g_kernel = gaussian_kernel(1,3)
[[0.07511361 0.1238414 0.07511361]
[0.1238414 0.20417996 0.1238414 ]
[0.07511361 0.1238414 0.07511361]]接下来用离散卷积的方法进行平滑滤波,即对原图扫描计算像素平均值
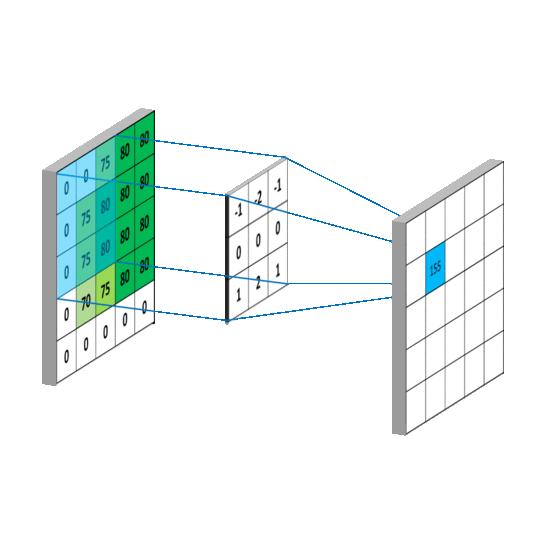
这里采用默认步长stride=1、padding=same,表示扫描每个像素点都做平滑,输出的矩阵大小和原图像大小相同。注意卷积运算是矩阵元素逆序相乘并求和,而python中np.multiply(A,B)函数(或点乘A*B)是数组对应元素顺序相乘,要利用这种乘法需要先将卷积核kernel旋转180°再进行运算,旋转函数np.rot90(m,k=1,axes=(0,1)),k>0代表逆时针旋转90°的次数,旋转2次即可
def smooth_convolve2d(arr, kernel, stride=1, padding
='same'):
Using convolution kernel to smooth 2D array / single channel image
Parameters
===========
arr: 2D array or single channel image
kernel: Filter matrix
stride: Stride of scanning
padding: padding mode
h, w = arr.shape
k, _ = kernel.shape
r = int(k/2)
kernel_r = np.rot90(kernel,k=2)
# padding outer area with 0
padding_arr = np.zeros([h+k-1,w+k-1])
padding_arr[r:h+r,r:w+r] = arr
new_arr = np.zeros([h,w])
for i in range(r,h+r,stride):
for j in range(r,w+r,stride):
roi = padding_arr[i-r:i+r+1,j-r:j+r+1]
new_arr[i-r][j-r] = np.sum(np.multiply(roi,kernel_r))
return new_arr
if __name__=='__main__':
g_kernel = gaussian_kernel(1,5)
A = np.zeros([10,10])
A[4:6,4:6] = 127
A1 = smooth_convolve2d(A,g_kernel)
plt.imshow(A,cmap='Greys')
plt.show()
plt.imshow(A1,cmap='Greys')
plt.show()
print(np.max(A))
print(np.max(A1))
计算梯度
边缘就是灰度值变化较大的的像素点的集合,灰度值变化程度和方向可以用梯度来表示。图片矩阵是离散的,这就可以按照向前差分格式计算梯度(一阶导数):
\frac{\partial f}{\partial x} = \frac{(f_{i,j+1}-f_{i,j})}{\triangle x} = (f_{i,j+1}-f_{i,j})\\ \frac{\partial f}{\partial y} = \frac{(f_{i+1,j}-f_{i,j})}{\triangle y}=(f_{i+1,j}-f_{i,j})\\
\triangle x = \triangle y = 1 均代表一个像素单位长度,转为矩阵运算形式如下
\frac{\partial }{\partial x} F = F\bullet A= \left[ \matrix{ f_{0,j}\\f_{1,j}\\f_{2,j}\\...\\f_{H-1,j} }\right]_{H\times W}\bullet \left[ \matrix{ -1\\1&-1\\&1&-1\\&&...&...\\&&&1&-1 }\right]_{W\times W} \\ \frac{\partial }{\partial y} F= B\bullet F=\left[ \matrix{ -1&1\\&-1&1\\&&-1&...\\&&&...&1\\&&&&-1 }\right]_{H\times H} \bullet \left[ \matrix{ f_{i,0}&f_{i,1}&...&f_{i,W-1} }\right]_{H\times W} \\
而梯度的幅值和方向则按照下列方式计算:
G_{i,j}=\sqrt{(\frac{\partial f}{\partial x}|_{i,j})^2+(\frac{\partial f}{\partial y}|_{i,j})^2}\\ \theta _{i,j}= arctan(\frac{\partial f}{\partial y}|_{i,j}/\frac{\partial f}{\partial x}|_{i,j})
梯度代码实现如下,delta取值范围只有 \left[ -\pi/2,\pi/2 \right] ,即只表达边界的单方向,不区分内外侧。
def gradients(arr_grey):
Get the gradients of each pixel.
Parameters
===========
arr_grey: grey image array
Returns
===========
Dx: gradient in the x direction
Dy: gradient in the y direction
G: gradient magnitude
Delta: gradient angle
H, W = arr_grey.shape
Ax = (-1)*np.eye(W,k=0) + (1)*np.eye(W,k=-1)
Ay = (-1)*np.eye(H,k=0) + (1)*np.eye(H,k=1)
Dx = np.dot(arr_grey,Ax)
Dy = np.dot(Ay,arr_grey)
G = (Dx**2 + Dy**2)**0.5
Delta = np.arctan(Dy/(Dx+1e-6))
return Dx, Dy, G, Delta
非极大值抑制NMS
在高斯滤波后,边缘有可能被放大了。这个步骤使用一个规则来过滤不是边缘的点,使边缘的宽度尽可能为1个像素点:遍历梯度矩阵上的所有点,并保留边缘方向上具有极大值的像素,其余点将灰度值设为0。
如果输入的是一个二值图像(黑白图像),即像素值只有0和1或者0和255,其得到的灰度矩阵极大值很均匀,则可以统一采用简单的单阈值判断 G[G<Target]=0 。
如果是普通灰度图像,边缘的梯度是局部极大值而非全局极大值,需要采用NMS算法(Non-Maximum Suppression)。
NMS 需要将当前的像素的梯度,与其他方向进行比较。g1,g2,g3,g4 分别是 8个相邻节点中的 4 个点,如果 g是局部最大值,g点的梯度幅值要大于梯度方向直线与 g1g2,g4g3 两个交点的梯度幅值,即大于点 dTemp1 和 dTemp2 的梯度幅值,dTemp1和dTemp可以通过线性插值求得:
weight = |gx| / |gy| or |gy| / |gx|
dTemp1 = weight*g1 + (1-weight)*g2
dTemp2 = weight*g3 + (1-weight)*g4当y 方向梯度值比较大时,|dy|>|dx|,weight = |dx| / |dy|,g1,g2,g3,g4如下图所示:
当前位置 g[i, j] ,g2 = g[i-1, j];g4 = g[i+1, j];
dx*dy< 0 时(左),g1 = d[i-1, j-1],g3 = d[i+1, j+1];
dx*dy\geq 0
时(右),g1 = d[i-1, j-1],g3 = d[i+1, j+1];

当x方向梯度值比较大时,|dx|>|dy|,weight = |dx| / |dy|,g1,g2,g3,g4如下图所示:
当前位置 g[i, j] ,g2 = g[i, j-1];g4 = g[i, j+1];
dx*dy< 0 时(左),g1 = d[i-1, j-1],g3 = d[i+1, j+1];
dx*dy\geq 0 时(右),g1 = d[i-1, j-1],g3 = d[i+1, j+1];

根据以上分类,代码实现如下:
def non_max_suppress(G,Dx,Dy):
W, H = G.shape
Gnms = np.copy(G)
Gnms[0, :] = Gnms[W-1, :] = Gnms[:, 0] = Gnms[:, H-1] = 0
# Traverse the inside nodes
for i in range(1, W-1):
for j in range(1, H-1):
# if G[i, j]<=1, then g is not the edge node
if G[i, j] <= 1:
Gnms[i, j] = 0
else:
# the gradient of current node
gx = Dx[i, j]
gy = Dy[i, j]
gTemp = G[i, j]
if np.abs(gy) > np.abs(gx):
weight = np.abs(gx) / np.abs(gy)
g2 = G[i-1, j]
g4 = G[i+1, j]
# g1 g2
# c
# g4 g3
if gx * gy < 0:
g1 = G[i-1, j-1]
g3 = G[i+1, j+1]
# g2 g1
# c
# g3 g4
else:
g1 = G[i-1, j+1]
g3 = G[i+1, j-1]
elif np.abs(gx) > np.abs(gy):
weight = np.abs(gy) / np.abs(gx)
g2 = G[i, j-1]
g4 = G[i, j+1]
# g3
# g2 c g4
if gx * gy> 0:
g1 = G[i+1, j-1]
g3 = G[i-1, j+1]
# g2 c g4
# g3
else:
g1 = G[i-1, j-1]
g3 = G[i+1, j+1]
# Use g1~g4 calculate gTemp
gTemp1 = weight * g1 + (1 - weight) * g2
gTemp2 = weight * g3 + (1 - weight) * g4
if gTemp >= gTemp1 and gTemp >= gTemp2:
Gnms[i, j] = gTemp
else:
Gnms[i, j] = 0
return Gnms
由于计算梯度采用了向前差分格式计算,所以局部可能存在不连续点(边缘向左或上方移动一个像素单位)。
双阈值检测
确定上下两个阀值,位于minVal之上的都可以作为候选边缘,梯度大于maxVal的任何边缘肯定是真边缘,介于minVal和maxVal之间的像素点,如果它们连接到“真边缘”像素,则它们被视为边缘的一部分,否则也会被丢弃,这样就可能提高准确度。

G节点邻域的8个节点中的最大值大于maxVal,则该节点与“真边缘”像素连通,代码实现如下:
DT = np.zeros(G.shape,dtype=np.int)
for i in range(1, W-1):
for j in range(1, H-1):
if (G[i, j] < TL):
DT[i, j] = 0
elif (G[i, j] > TH):
DT[i, j] = 1 # true edge
# if connected
elif (G[i-1, j-1:j+1] < TH).any() or (G[i+1, j-1:j+1].any()
or (G[i, [j-1, j+1]] < TH).any()):
DT[i, j] = 1
考虑到Python语言的特性,使用双重for-loop遍历整个图片会增加耗时和不必要的节点操作,而边缘节点只占整个数组的少量区域,因此将其转换为numpy数组切片和索引的操作以加快运算效率,采用np.where得到候选边缘的索引数组,使用单层for循环遍历较小的一维数组即可
def threshold_double(g,c1=0.1,c2=0.5):
H, W = g.shape
DT = np.zeros(g.shape,dtype=np.int8)
TL = c1*np.max(g)
TH = c2*np.max(g)
# Find index of G where g>TL and g<=TH
DT[g>TH] = 1
x,y = np.where(g>TL)
for i in range(len(x)):
roi = g[x[i]-1:x[i]+2,y[i]-1:y[i]+2]
if roi.any()>=TH:
DT[x[i],y[i]] = 1
return DT对于200x200大小的单通道图片,采用for循环遍历和数组索引方式的运行时间分别为0.018s和0.002s,效率提升接近10倍。
测试结果对比
把前面的函数封装一下,跟opencv做个对比
def myCanny(img,c1=0.1,c2=0.5):
gx, gy, g, delta = gradients(img)
gnms = non_max_suppress(g,gx,gy)
if c2 > 1: # if input pixel value
c1 = c1/255
c2 = c2/255
dst = threshold_double(g,c1,c2)
return dstOpenCV-Python中Canny函数的原型如下,image参数即为需要处理的单通道的灰度图,threshold1、threshold2 即对应下阈值 TL 上阈值 TH 。
import cv2
cv2.Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient ]]]) 处理同一张图片看看效果:
if __name__=='__main__':
# Use myCanny
img = plt.imread('cat1.png')
grey = img_grey(img)
plt.imshow(img)
plt.axis('off')
plt.show()
kernel = gaussian_kernel(0.8,5)
img_new = smooth_convolve2d(grey,kernel)
canny = myCanny(img_new,30,127)
plt.imshow(canny,cmap="gray")
plt.axis('off')
plt.show()
# Use opencv canny
img2 = cv2.imread('cat1.png')
img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB) # cv2默认为bgr顺序
