常见的损失函数(loss function)总结

损失函数 用来评价模型的 预测值 和 真实值 不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。

损失函数 分为 经验风险损失函数 和 结构风险损失函数 。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。

常见的损失函数以及其优缺点如下：

1. 0-1损失函数(zero-one loss)

0-1损失是指预测值和目标值不相等为1， 否则为0:

L ( Y , f ( X ) ) = \left\{ \begin{array} { l } { 1 , Y \neq f ( X ) } \\ { 0 , Y = f ( X ) } \end{array} \right. \\

特点：

(1)0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用.

(2) 感知机 就是用的这种损失函数。但是相等这个条件太过严格，因此可以放宽条件，即满足 |Y - f(x)| < T 时认为相等，

L ( Y , f ( X ) ) = \left\{ \begin{array} { l } { 1 , | Y - f ( X ) | \geq T } \\ { 0 , | Y = f ( X ) | < T } \end{array} \right. \\

2. 绝对值损失函数

绝对值损失函数是计算预测值与目标值的差的绝对值：

L(Y, f(x)) = |Y - f(x)| \\

3. log对数损失函数

log对数损失函数 的标准形式如下：

L(Y, P(Y|X)) = -logP(Y|X) \\

特点：

(1) log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。

(2)健壮性不强，相比于hinge loss对噪声更敏感。

(3) 逻辑回归 的损失函数就是log对数损失函数。

4. 平方损失函数

平方损失函数标准形式如下：

L ( Y | f ( X ) ) = \sum _ { N } ( Y - f ( X ) ) ^ { 2 } \\

特点：

(1)经常应用与回归问题

5. 指数损失函数（exponential loss）

指数损失函数 的标准形式如下：

L(Y|f(X)) = exp[-yf(x)] \\

特点：

(1)对离群点、噪声非常敏感。经常用在AdaBoost算法中。

6. Hinge 损失函数

Hinge损失函数标准形式如下：

L(y, f(x)) = max(0, 1-yf(x)) \\

特点：

(1)hinge损失函数表示如果被分类正确，损失为0，否则损失就为 1-yf(x) 。 SVM 就是使用这个损失函数。

(2)一般的 f(x) 是预测值，在-1到1之间， y 是目标值(-1或1)。其含义是， f(x) 的值在-1和+1之间就可以了，并不鼓励 |f(x)| > 1 ，即并不鼓励分类器过度自信，让某个正确分类的样本距离分割线超过1并不会有任何奖励，从而 使分类器可以更专注于整体的误差。

(3) 健壮性相对较高，对异常点、噪声不敏感，但它没太好的概率解释。

7. 感知损失(perceptron loss)函数

感知损失函数 的标准形式如下：

L(y, f(x)) = max(0, -f(x)) \\

特点：

(1)是Hinge损失函数的一个变种，Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron loss 只要样本的判定类别正确的话，它就满意，不管其判定边界的距离 。它比Hinge loss简单，因为不是max-margin boundary，所以模 型的泛化能力没 hinge loss强 。

8. 交叉熵损失函数 (Cross-entropy loss function)

交叉熵损失函数 的标准形式如下 :

C = - \frac { 1 } { n } \sum _ { x } [ y \ln a + ( 1 - y ) \ln ( 1 - a ) ] \\

注意公式中 x 表示样本， y 表示实际的标签， a 表示预测的输出， n 表示样本总数量。

特点：

(1)本质上也是一种 对数似然函数 ，可用于二分类和多分类任务中。

二分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：

loss = - \frac { 1 } { n } \sum _ { x } [ y \ln a + ( 1 - y ) \ln ( 1 - a ) ] \\

多分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）：

loss = - \frac{1}{n} \sum_i y_ilna_i \\

(2)当使用sigmoid作为激活函数的时候，常用 交叉熵损失函数 而不用 均方误差损失函数 ，因为它可以 完美解决平方损失函数权重更新过慢 的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。

最后奉献上交叉熵损失函数的实现代码： cross_entropy .

---

这里需要更正一点， 对数损失函数和交叉熵损失函数应该是等价的！！！ （此处感谢 @Areshyy 的指正，下面说明也是由他提供）

下面来具体说明：

---

相关高频问题：

1. 交叉熵函数 与 最大似然函数 的联系和区别？

区别： 交叉熵函数 使用来描述模型预测值和真实值的差距大小，越大代表越不相近； 似然函数 的本质就是衡量在某个参数下，整体的估计和真实的情况一样的概率，越大代表越相近。

联系： 交叉熵函数 可以由最大似然函数在伯努利分布的条件下推导出来，或者说 最小化交叉熵函数 的本质就是 对数似然函数的最大化 。

怎么推导的呢？我们具体来看一下。

设一个随机变量 X 满足伯努利分布，

P(X=1) = p, P(X=0)=1-p \\

则 X 的概率密度函数为：

P(X)=p^X(1-p)^{1-X} \\

因为我们只有一组采样数据 D ，我们可以统计得到 X 和 1-X 的值，但是 p 的概率是未知的，接下来我们就用 极大似然估计 的方法来估计这个 p 值。

对于采样数据 D ，其 对数似然函数 为:

logP(D) = log\prod_{i}^{N}P(D_i) \\ = \sum_{i}logp(D_i) \\ = \sum_{i}(D_ilogp + (1-D_i)log(1-p)) \\

可以看到上式和 交叉熵函数 的形式几乎相同， 极大似然估计 就是要求这个式子的最大值。而由于上面函数的值总是小于0，一般像神经网络等对于损失函数会用最小化的方法进行优化，所以一般会在前面加一个负号，得到 交叉熵函数 （或 交叉熵损失函数 ）：

loss = -\sum_{i}(D_ilogp + (1-D_i)log(1-p)) \\

这个式子揭示了 交叉熵函数 与 极大似然估计 的联系， 最小化交叉熵函数 的本质就是 对数似然函数的最大化。

现在我们可以用求导得到极大值点的方法来求其 极大似然估计 ，首先将对数似然函数对 p 进行求导，并令导数为0，得到

\sum_{i}(D_i \frac{1}{p} + (1-D_i) \frac{1}{p-1}) =0 \\

消去分母，得：

\sum_{i}^{N}(p-D_i) = 0 \\

所以:

p = \frac{1}{N} \sum_i D_i \\

这就是伯努利分布下 最大似然估计 求出的概率 p 。

2. 在用sigmoid作为激活函数的时候，为什么要用 交叉熵损失函数 ，而不用 均方误差损失函数 ？

其实这个问题求个导，分析一下两个误差函数的参数更新过程就会发现原因了。

对于 均方误差损失函数 ，常常定义为：

C= \frac{1}{2n}\sum_x(a - y)^2 \\

其中 y 是我们期望的输出， a 为神经元的实际输出（ a = \sigma(z), z=wx+b ）。在训练神经网络的时候我们使用梯度下降的方法来更新 w 和 b ，因此需要计算代价函数对 w 和 b 的导数：

\frac{\partial C }{\partial w} = (a-y)\sigma'(z)x \\ \frac{\partial C }{\partial b } = (a-y)\sigma'(z)\\

然后更新参数 w 和 b ：

w = w - \eta \frac{\partial C}{\partial w} = w - \eta (a-y)\sigma'(z)x \\ b = b - \eta \frac{\partial C}{\partial b} = b - \eta (a-y)\sigma'(z) \\

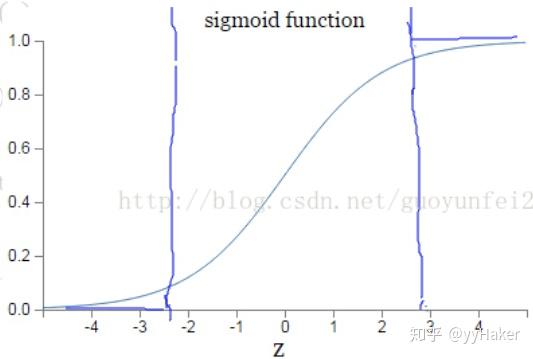
因为sigmoid的性质，导致 \sigma'(x) 在 z 取大部分值时会很小（如下图标出来的两端，几乎接近于平坦），这样会使得 \eta (a-y)\sigma'(z) 很小，导致参数 w 和 b 更新非常慢。

那么为什么 交叉熵损失函数 就会比较好了呢？同样的对于 交叉熵损失函数 ，计算一下参数更新的梯度公式就会发现原因。 交叉熵损失函数 一般定义为：

C = - \frac { 1 } { n } \sum _ { x } [ y \ln a + ( 1 - y ) \ln ( 1 - a ) ] \\

其中 y 是我们期望的输出， a 为神经元的实际输出（ a = \sigma(z), z=wx+b ）。同样可以看看它的导数：

\frac{\partial C}{\partial a} = -\frac{1}{n}\sum_x[y\frac{1}{a}+(y-1)\frac{1}{1-a}] \\ = -\frac{1}{n}\sum_x[\frac{1}{a(1-a)}y - \frac{1}{1-a}] \\ = -\frac{1}{n}\sum_x[\frac{1}{\sigma(x)(1-\sigma(x))}y - \frac{1}{1-\sigma(x)}] \\

另外，

\frac{\partial C}{\partial z} = \frac{\partial C}{\partial a} \frac{\partial a}{\partial z} \\ =-\frac{1}{n}\sum_x[\frac{1}{\sigma(x)(1-\sigma(x))}y - \frac{1}{1-\sigma(x)}] \bullet \sigma'(x) \\ = -\frac{1}{n}\sum_x[\frac{1}{\sigma(x)(1-\sigma(x))}y - \frac{1}{1-\sigma(x)}]\bullet \sigma(x)(1-\sigma(x)) \\ = -\frac{1}{n} \sum_x(y-a) \\

所以有：

\frac{\partial C}{\partial w} = \frac{\partial C}{\partial z} \frac{\partial z}{\partial w} = (a-y)x \\

\frac{\partial C}{\partial b} = \frac{\partial C}{\partial z} \frac{\partial z}{\partial b} = (a-y) \\

所以参数更新公式为：

w = w - \eta \frac{\partial C}{\partial w} = w - \eta (a-y)x\\ b = b - \eta \frac{\partial C}{\partial b} = b - \eta (a-y) \\

可以看到参数更新公式中没有 \sigma'(x) 这一项，权重的更新受 (a-y) 影响，受到误差的影响，所以 当误差大的时候，权重更新快；当误差小的时候，权重更新慢 。这是一个很好的性质。

所以当使用sigmoid作为激活函数的时候，常用 交叉熵损失函数 而不用 均方误差损失函数 。