首先,我们先来看一下什么是Networks(网络)。
Networks are a general language for describing complex systems of interating entities.
网络是一种描述复杂系统中关联实体的通用语言。
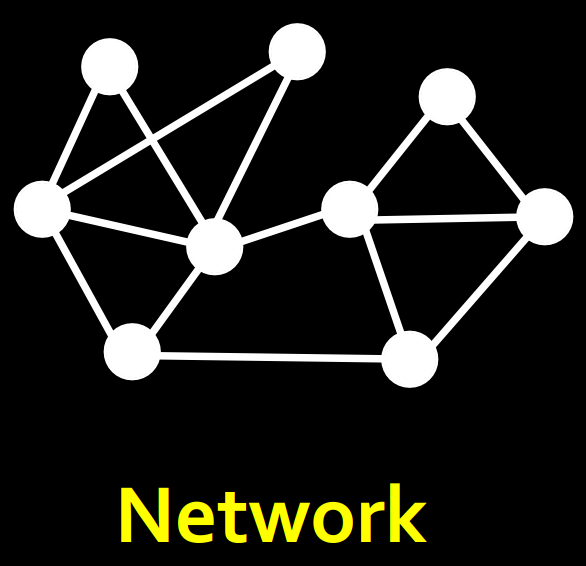
那么,对于这样的一种“通用语言”,我们不禁会产生两个问题:
-
How are these system organized?
-
What are their design properties?
我们只有弄清楚这些系统背后的网络模型,才有可能真正地对这些系统进行建模、解析、预测、深度利用。
在我们的生活中,其实很多数据都是以网络/图的形式存在的。网络可以大致分为两类,不过这两类网络有时候界限没有那么明显:
-
Networks (Natural Graphs)
第一类可以看做是自然网络,比如社会、社交网络、蛋白质图谱、基因图谱、思维导图等。
-
Information Graphs
第二类就是各种信息汇聚成为的网络,如知识图谱,相似网络(similarity netoworks)等等。
那么,为什么要研究网络呢?
主要有下面几点原因:

目前对于网络的研究主要集中在以下几个方面/场景:
-
对节点的类型/属性进行预测。例如:节点分类。
-
预测两个节点是否相连。例如:链路预测(link prediction)。
-
识别紧密相连的节点群。例如:社区挖掘(Community detection),节点聚类。
-
计算两个节点或者网络的相似性。
网络(Networks)的结构使怎么样的呢?我们先来看一下它的定义:
A network is a collection of objects where some pairs of objects are connected by links
网络是互连成对的节点的集合。
网络的结构有三类重要的元素:
-
Objects(对象):Nodes(节点)、顶点(Vertices),用
G
(
N
,
E
)
来表示。
那么,构建一个网络/图,就是定义它的这些基本结构——哪些信息/元素作为节点,这些节点之间怎么进行连接(即边怎么定义)。对于不同的场景,选择合适的图来进行描述和建模,会变得事半功倍。
同时,很多时候,图的结构使不唯一的,你怎么定义图的结构,取决于你要研究/解决什么问题。
有向图和无向图
|
|
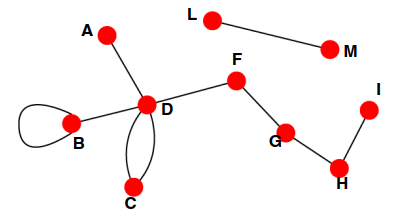
无向图
|
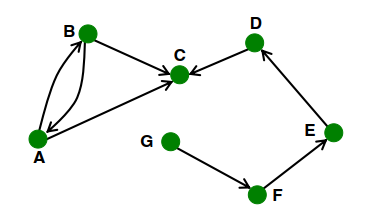
有向图
|
|
图例
|
|
|
|
特点
|
undirected (symmetrical, reciprocal)
|
directed (arcs)
|
|
例子
|
合作关系,微信中的好友关系
|
微博上的follow关系
|
|
度(Node degrees)
|
在无向图中,点的度为与其相连的边的数量。如图中D点的度
k
i
n
=
k
o
u
t
。
|
完全图(Complete Graph)
在图论的数学领域,完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
二分图(Bipartite graph,二部图,对偶图)
|
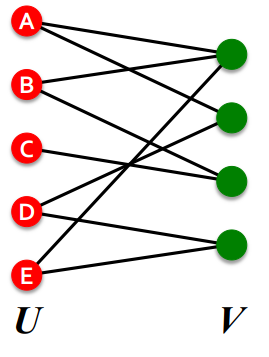
二分图
|
二分图的折叠(folded) /投影(projection)
|
|
|
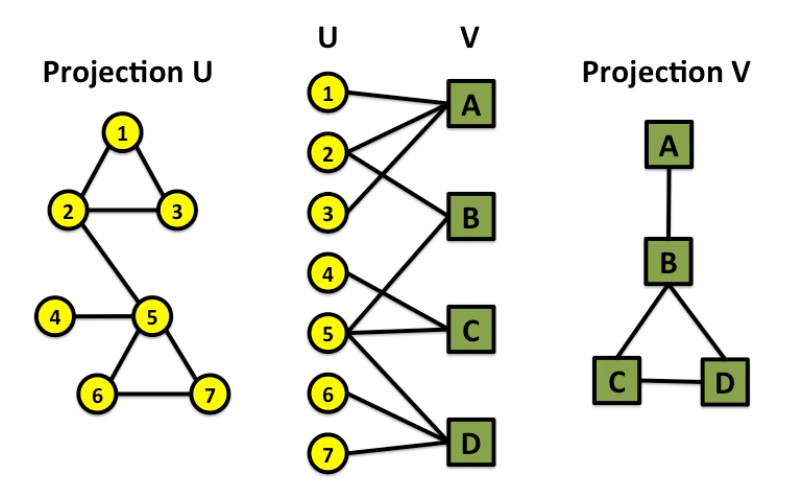
在二分图中,图的节点恰好可以分为两个互不相交的集合
V
,图中每条边都是这两个集合中的节点的链接。二分图是一种十分常见的图数据对象,描述了两类对象之间的交互关系,如:用户与商品,作者与文章。
二分图的折叠(folded) /投影(projection)
是指若该集合中的某些节点如果有链接到另一个集合的同一个节点,则认为他们之间存在一定的关系。
加权图(Weighted graph)与非加权图(Unweighted graph)
连通图与非连通图
如果图中存在孤立的顶点,没有任何边与之相连,这样的图被称为非连通图。反之,如果不存在孤立顶点的图称为连通图。
其他类型的图
邻接矩阵(Adjacency matrix)
邻接矩阵中
{
(
1
,
4
)
,
(
2
,
1
)
,
(
4
,
2
)
,
(
4
,
3
)
}
。
邻接列表(Adjacency list)
当图变得很大、邻接矩阵很稀疏时,使用邻接列表对图进行存储是一个不错的选择。邻接列表实质上是一个
dict
。例如:
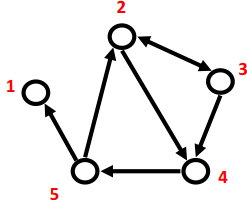
上图的邻接列表为
{1:[], 2:[3,4], 3:[2,4], 4:[5], 5:[1,2]}
。
课程链接:CS224W: Machine Learning with Graphs课程视频:【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)目录0. 写在前面1. Why Networks?2. 基础:网络/图论基本知识2.1 Starter Topic: Structure of Graphs 图的结构2.2 Choice of Network Representation 图的不同形式0. 写在前面第一节课是Introduction,主要介绍了图的优势以及图论的一些基本.
图
神经网络
系列- 斯坦福
CS224W
《
图
机器
学习
》-
学习
笔记
2
学习
笔记
1
https://blog.csdn.net/duan_zhihua/article/details/116242732?spm=1001.2014.3001.5501
目录
网络
表示度分布
图
路径
图
的直径
图
聚类系数
图
的连通分量
网络
表示
如何评估衡量一个
网络
?可以用以下属性来表示:
度分布(Degree distribut
ion
) P ( k )
路径长度 h
聚类系数(Clustering coefficient)
连通组件(C
CS224W
课程
笔记
。
这些注释使用Markdown编写,并使用Jekyll编译为HTML。 请直接将您的更改添加到Markdown源代码中。 此仓库未配置任何额外的Jekyll插件,因此可以直接由GitHub Pages进行编译。 因此,对Markdown文件的任何更改都将自动反映在实时网站中。
要对此仓库进行任何更改,请先分叉此仓库。 进行所需的更改,然后将其推送到此存储库的自己的分叉副本中。 最后,返回GitHub网站以创建请求请求,以将您的更改带入snap-stanford/
cs224w
-notes回购中。
如果要在将更改推送到master分支之前在本地测试更改,则可以在自己的计算机上本地运行Jekyll。 为了安装Jekyll,您可以按照其网站( )上发布的说明进行操作。 然后,从此仓库的克隆版本的根目录执行以下操作:
对Markdown
CS224W
-
图
神经网络
笔记
1:
Int
roduct
ion
: Structure of Graphs
本文总结之日
CS224W
W
int
er 2021只更新到了第四节,所以下文会参考2021年课程的PPT并结合2019年秋季课程进行总结以求内容完整
课程主页:
CS224W
: Machine Learning with Graphs
视频链接:【斯坦福】
CS224W
:
图
机器
学习
( 中英字幕 | 2019秋)
文章目录
CS224W
-
图
神经网络
笔记
1:
Int
roduct
ion
: Structure of
文章目录
cs224w
(一)
Int
roduct
ion
;Structure of GraphsWhy Networks?
网络
/
图
的类型
网络
和应用
图
的结构
图论
的一些概念
图
的表示邻接矩阵边列表邻接表边的权重
图
的其他类型
图
的连通性
cs224w
(一)
Int
roduct
ion
;Structure of Graphs
Why Networks?
网络
是描述相互作用实体的复杂系统的通用语言
在许多系统背后,有一个复杂的
网络
,它定义了组件之间的相互作用。除非我们了解这些系统背后的
网络
,否则我们永远无法对它们进行建模和预测
论文地址:Dual-Primal Graph Convolut
ion
al Networks
这篇论文的主要工作是通过构建对偶
图
Dual Graph的方式将原
图
的边转换成对偶
图
中的节点,从而获得edge embedding。
什么是对偶
图
?
原文中给出了这样的解释:
Let G=(V,E)\mathcal{G}=(\mathcal{V}, \mathcal{E})G=(V,E)be a given directed graph, to which we refer as the primal graph.
什么是
图
?
图
是由一些点和一些线构成的,能表示一些实体之间的关系,
图
中的点就是实体,线就是实体间的关系。如下
图
,v就是顶点,e是边,u是整张
图
。attrinbutes是信息的意思,每个点、每条边、每个
图
都是有信息的。
怎么表示一张
图
,可以参考下面这个例子
每个顶点、边和整张
图
都可以用一个向量来表示,在这个例子中,顶点的向量有六个值,柱体的高矮就表示该值的.
Dual Graph enhanced Embedding Neural Network for CTR
Predict
ion
Wei Guo, Rong Su, Renhao Tan, Huifeng Guo, Yingxue Zhang, Zhirong Liu,
Ruiming Tang, Xiuqiang HeHuawei Noah’s Ark Labhttps://arxiv.org/pd...
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录前言一、为什么要选择
图
进行机器
学习
?(起源)1.现代深度
学习
工具的不足二、
图
神经网络
定义1.引入库2.读入数据总结
提示:这里可以添加本文要记录的大概内容:
本章主要介绍了
图
神经网络
的起源、定义、应用与总结。
课程建议先修知识点: 1.机器
学习
、2.算法与
图论
、3.概率论与数理统计
一、为什么要选择
图
进行机器
学习
?(起源)
图
是用于描述并分析有关联/互动的实体的一种普适语言。它不将实体视为一系列孤立的点,而认为其互相之间.
Networks (also known as Natural Graphs)
社会(Society )是70多亿人的集合;
通信系统(Communicat
ion
systems)连接了各种电子设备;
基因/蛋白质( genes/proteins)之间...
【机器
学习
】层次聚类-Agglomerative clustering
Agglomerative clustering从NNN个簇开始,每个簇最初只包含一个对象,然后在每个步骤中合并两个最相似的簇,直到形成一个包含所有数据的簇。
合并过程可以用二叉树(binary tree) 表示,称为树状
图
(dendrogram)。初始簇位于叶节点(
图
的底部),每当两个簇合并时,我们就将它们联接到树中。分支的...
文章目录0 章节前言
图
的两种特征数据传统机器
学习
Pipeline本章内容概览1 Tradit
ion
al Feature-based Method- Node1. 问题描述:根据已有的红绿色信息,预测灰色点的颜色信息2. 首要问题:使用何种features描述节点的**位置和结构**信息
0 章节前言
图
的两种特征数据
节点和边的attribute和property
描述了
图
的拓扑结构的数据
传统机器
学习
Pipeline
设计、获取特征
本章内容概览
使用高效的feature是好性能
Network: Networks are a general language for describing complex systems of
int
eracting entities.
Two types of Networks/Graphs:
Networks(also known as Natural Graphs):
Society; Communicat
ion
system;
Int
eract
ion
s between genes regulate life; thoughts
Informa






