Prophet是Facebook公司开源的一款时间序列预测模型接口,可用R语言或python进行相关时间预测操作,本文将会从它的代码上对其进行模型拟合以及预测的过程进行一个梳理,并使用python中的pymc包进行Stan文件中贝叶斯建模的复现。
一、数据预处理阶段:
(一)setup_dataframe
(二)set_auto_seasonalities
(三)make_all_seasonality_features
二、贝叶斯建模
(一)、趋势项
(二)、季节因素
四、pymc模型效果实
一、数据预处理阶段:
此时主要有3个函数进行了数据的预处理以及特征提取操作:
(一)setup_dataframe
这一函数主要是对要进行训练的DataFrame做数据检验及标准化操作:
1、检验DataFrame的时间列以及是否合法
2、检验使用add_regressor函数增加的外部变量是否合法
3、检验使用add_seasonaliy函数增加的季节性因素是否合法
4、重设index并对时间序列数据做标准化
def setup_dataframe(self, df, initialize_scales=False):
"""Prepare dataframe for fitting or predicting.
Adds a time index and scales y. Creates auxiliary columns 't', 't_ix',
'y_scaled', and 'cap_scaled'. These columns are used during both
fitting and predicting.
Parameters
----------
df: pd.DataFrame with columns ds, y, and cap if logistic growth. Any
specified additional regressors must also be present.
initialize_scales: Boolean set scaling factors in self from df.
Returns
-------
pd.DataFrame prepared for fitting or predicting.
#检验DataFrame的各列是否合法
if 'y' in df: # 'y' will be in training data
df['y'] = pd.to_numeric(df['y'])
if np.isinf(df['y'].values).any():
raise ValueError('Found infinity in column y.')
if df['ds'].dtype == np.int64:
df['ds'] = df['ds'].astype(str)
df['ds'] = pd.to_datetime(df['ds'])
if df['ds'].dt.tz is not None:
raise ValueError(
'Column ds has timezone specified, which is not supported. '
'Remove timezone.'
if df['ds'].isnull().any():
raise ValueError('Found NaN in column ds.')
for name in self.extra_regressors: #add_regressor会增加extra_regressors,表明那一列作为额外的回归量,可以是乘法也可以是加法
if name not in df:
raise ValueError(
'Regressor {name!r} missing from dataframe'
.format(name=name)
df[name] = pd.to_numeric(df[name])
if df[name].isnull().any():
raise ValueError(
'Found NaN in column {name!r}'.format(name=name)
for props in self.seasonalities.values(): #如果没有add_seasonality的话,fit时不会有用,因为这时self.seasonalities没有初始化
condition_name = props['condition_name']
if condition_name is not None:
if condition_name not in df:
raise ValueError(
'Condition {condition_name!r} missing from dataframe'
.format(condition_name=condition_name)
if not df[condition_name].isin([True, False]).all():
raise ValueError(
'Found non-boolean in column {condition_name!r}'
.format(condition_name=condition_name)
df[condition_name] = df[condition_name].astype('bool')
if df.index.name == 'ds':#重设index
df.index.name = None
df = df.sort_values('ds')
df = df.reset_index(drop=True)
self.initialize_scales(initialize_scales, df) #对extra_regressor进行标准化做前置准备
# 进行标准化
if self.logistic_floor:
if 'floor' not in df:
raise ValueError('Expected column "floor".')
else:
df['floor'] = 0
if self.growth == 'logistic':
if 'cap' not in df:
raise ValueError(
'Capacities must be supplied for logistic growth in '
'column "cap"'
if (df['cap'] <= df['floor']).any():
raise ValueError(
'cap must be greater than floor (which defaults to 0).'
df['cap_scaled'] = (df['cap'] - df['floor']) / self.y_scale
df['t'] = (df['ds'] - self.start) / self.t_scale
if 'y' in df:
df['y_scaled'] = (df['y'] - df['floor']) / self.y_scale
for name, props in self.extra_regressors.items():
df[name] = ((df[name] - props['mu']) / props['std'])
return df
(二)set_auto_seasonalities
这个函数的作用,是根据数据的时间间隔分别判断是否有Yearly Weekly以及Daily的周期效应并给出内置的对应参数为下一个对季节性因素分解的函数make_all_seasonality_features作准备。
def set_auto_seasonalities(self):
"""Set seasonalities that were left on auto.
Turns on yearly seasonality if there is >=2 years of history.
Turns on weekly seasonality if there is >=2 weeks of history, and the
spacing between dates in the history is <7 days.
Turns on daily seasonality if there is >=2 days of history, and the
spacing between dates in the history is <1 day.
first = self.history['ds'].min()
last = self.history['ds'].max()
dt = self.history['ds'].diff()
min_dt = dt.iloc[dt.values.nonzero()[0]].min()
# Yearly seasonality
yearly_disable = last - first < pd.Timedelta(days=730)
fourier_order = self.parse_seasonality_args(
'yearly', self.yearly_seasonality, yearly_disable, 10)
if fourier_order > 0:
self.seasonalities['yearly'] = {
'period': 365.25,
'fourier_order': fourier_order,
'prior_scale': self.seasonality_prior_scale,
'mode': self.seasonality_mode,
'condition_name': None
# Weekly seasonality
weekly_disable = ((last - first < pd.Timedelta(weeks=2)) or
(min_dt >= pd.Timedelta(weeks=1)))
fourier_order = self.parse_seasonality_args(
'weekly', self.weekly_seasonality, weekly_disable, 3)
if fourier_order > 0:
self.seasonalities['weekly'] = {
'period': 7,
'fourier_order': fourier_order,
'prior_scale': self.seasonality_prior_scale,
'mode': self.seasonality_mode,
'condition_name': None
# Daily seasonality
daily_disable = ((last - first < pd.Timedelta(days=2)) or
(min_dt >= pd.Timedelta(days=1)))
fourier_order = self.parse_seasonality_args(
'daily', self.daily_seasonality, daily_disable, 4)
if fourier_order > 0:
self.seasonalities['daily'] = {
'period': 1,
'fourier_order': fourier_order,
'prior_scale': self.seasonality_prior_scale,
'mode': self.seasonality_mode,
'condition_name': None
(三)make_all_seasonality_features
这个函数就是主要将set_auto_seasonalities中给出的各个季节项信息以及节假日因素作出分解并提取特征。
对于季节项信息,主要是调用fourier_series这个函数对各个不同季节信息对应的series_order与peirod做傅里叶变换,其中sieries_order代表要分解出来的序列数量,而peirod代表了季节对应的周期。
def fourier_series(
dates: pd.Series,
period: Union[int, float],
series_order: int,
) -> NDArray[np.float_]:
"""Provides Fourier series components with the specified frequency
and order.
Parameters
----------
dates: pd.Series containing timestamps.
period: Number of days of the period.
series_order: Number of components.
Returns
-------
Matrix with seasonality features.
if not (series_order >= 1):
raise ValueError("series_order must be >= 1")
# convert to days since epoch
t = dates.to_numpy(dtype=np.int64) // NANOSECONDS_TO_SECONDS / (3600 * 24.)
x_T = t * np.pi * 2
fourier_components = np.empty((dates.shape[0], 2 * series_order))
for i in range(series_order):
c = x_T * (i + 1) / period
fourier_components[:, 2 * i] = np.sin(c)
fourier_components[:, (2 * i) + 1] = np.cos(c)
return fourier_components
此处简单举个例子:
Prophet自带的Yearly参数为例,其中sieries_order为10,代表要分解出10个序列;period为365.25,表示一个周期的长度(也就是频率)为365.25。此处使用的傅里叶级数公式为:
其中,t为标准化到“日”的时间点信息,p为period,是个固定值,而n就代表了当前的series_order,从1到10不等,可以看做是傅里叶级数的阶数。将其正弦项和余弦项作图打印出来,如图所示: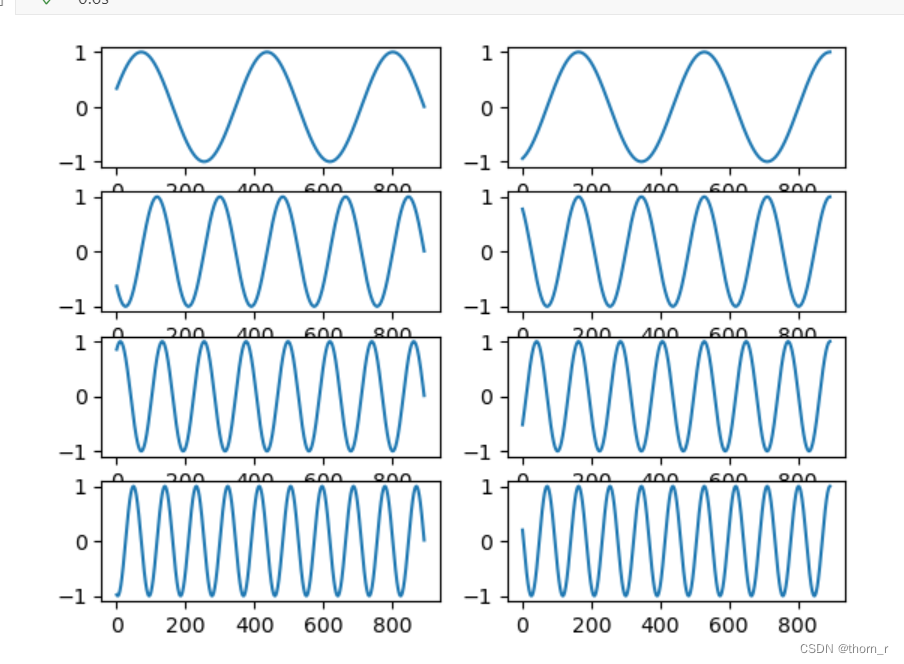
最终,能够得到20个关于年份的正弦/余弦函数特征。
而对于节假日信息的处理则较为简单,就是单纯地对每个节假日的时间点以及我们在初始化时填写的"upper_window"与"lower_window"的偏移量的位置做0-1变量特征:
def make_holiday_features(self, dates, holidays):
"""Construct a dataframe of holiday features.
Parameters
----------
dates: pd.Series containing timestamps used for computing seasonality.
holidays: pd.Dataframe containing holidays, as returned by
construct_holiday_dataframe.
Returns
-------
holiday_features: pd.DataFrame with a column for each holiday.
prior_scale_list: List of prior scales for each holiday column.
holiday_names: List of names of holidays
# Holds columns of our future matrix.
expanded_holidays = defaultdict(lambda: np.zeros(dates.shape[0]))
prior_scales = {}
# Makes an index so we can perform `get_loc` below.
# Strip to just dates.
row_index = pd.DatetimeIndex(dates.dt.date)
for row in holidays.itertuples():
dt = row.ds.date()
lw = int(getattr(row, 'lower_window', 0))
uw = int(getattr(row, 'upper_window', 0))
except ValueError:
lw = 0
uw = 0
ps = float(getattr(row, 'prior_scale', self.holidays_prior_scale))
if np.isnan(ps):
ps = float(self.holidays_prior_scale)
if row.holiday in prior_scales and prior_scales[row.holiday] != ps:
raise ValueError(
'Holiday {holiday!r} does not have consistent prior '
'scale specification.'.format(holiday=row.holiday)
if ps <= 0:
raise ValueError('Prior scale must be > 0')
prior_scales[row.holiday] = ps
for offset in range(lw, uw + 1):
occurrence = pd.to_datetime(dt + timedelta(days=offset))
loc = row_index.get_loc(occurrence)
except KeyError:
loc = None
key = '{}_delim_{}{}'.format(
row.holiday,
'+' if offset >= 0 else '-',
abs(offset)
if loc is not None:
expanded_holidays[key][loc] = 1.
else:
expanded_holidays[key] # Access key to generate value
holiday_features = pd.DataFrame(expanded_holidays)
# Make sure column order is consistent
holiday_features = holiday_features[sorted(holiday_features.columns
.tolist())]
prior_scale_list = [
prior_scales[h.split('_delim_')[0]]
for h in holiday_features.columns
holiday_names = list(prior_scales.keys())
# Store holiday names used in fit
if self.train_holiday_names is None:
self.train_holiday_names = pd.Series(holiday_names)
return holiday_features, prior_scale_list, holiday_names
举个简单的例子,我们将店铺促销的日子作为Holiday传入模型,upper_window与lower_window设置为2,最后模型的特征就会增加5列,分别是:是否当日为促销,是否当日为促销前1天/前2天/后1天/后2天
holiday_df = pd.DataFrame({
"holiday":"Promo",
"ds":tmp[tmp.Promo==1].Date,
"upper_window":2,
"lower_window":-2
最终,将傅里叶级数的季节性因素、节假日因素以及使用add_aggressor添加的外部因素3个的特征融合,获得特征矩阵。
除此之外,还有一个regressor_column_matrix函数,用以表示特征矩阵的哪些列对应于哪些季节性/回归分量的数据框。
def regressor_column_matrix(self, seasonal_features, modes):
"""Dataframe indicating which columns of the feature matrix correspond
to which seasonality/regressor components.
Includes combination components, like 'additive_terms'. These
combination components will be added to the 'modes' input.
Parameters
----------
seasonal_features: Constructed seasonal features dataframe
modes: Dictionary with keys 'additive' and 'multiplicative' listing the
component names for each mode of seasonality.
Returns
-------
component_cols: A binary indicator dataframe with columns seasonal
components and rows columns in seasonal_features. Entry is 1 if
that columns is used in that component.
modes: Updated input with combination components.
components = pd.DataFrame({
'col': np.arange(seasonal_features.shape[1]),
'component': [
x.split('_delim_')[0] for x in seasonal_features.columns
# Add total for holidays
if self.train_holiday_names is not None:
components = self.add_group_component(
components, 'holidays', self.train_holiday_names.unique())
# Add totals additive and multiplicative components, and regressors #将所有的holiday视作同一效应作为holiday的total效应,下additive与multiplicative相同
for mode in ['additive', 'multiplicative']:
components = self.add_group_component(
components, mode + '_terms', modes[mode]
regressors_by_mode = [
r for r, props in self.extra_regressors.items()
if props['mode'] == mode
components = self.add_group_component(
components, 'extra_regressors_' + mode, regressors_by_mode)
# Add combination components to modes
modes[mode].append(mode + '_terms')
modes[mode].append('extra_regressors_' + mode)
# After all of the additive/multiplicative groups have been added,
modes[self.seasonality_mode].append('holidays')
# Convert to a binary matrix 将components表转置成为0-1变量的查询表
component_cols = pd.crosstab(
components['col'], components['component'],
).sort_index(level='col')
# Add columns for additive and multiplicative terms, if missing
for name in ['additive_terms', 'multiplicative_terms']:
if name not in component_cols:
component_cols[name] = 0
# Remove the placeholder
component_cols.drop('zeros', axis=1, inplace=True, errors='ignore')
# Validation
if (max(component_cols['additive_terms']
+ component_cols['multiplicative_terms']) > 1):
raise Exception('A bug occurred in seasonal components.')
# Compare to the training, if set.
if self.train_component_cols is not None:
component_cols = component_cols[self.train_component_cols.columns]
if not component_cols.equals(self.train_component_cols):
raise Exception('A bug occurred in constructing regressors.')
return component_cols, modes
完整代码如下:
def make_all_seasonality_features(self, df):
"""Dataframe with seasonality features.
Includes seasonality features, holiday features, and added regressors.
Parameters
----------
df: pd.DataFrame with dates for computing seasonality features and any
added regressors.
Returns
-------
pd.DataFrame with regression features.
list of prior scales for each column of the features dataframe.
Dataframe with indicators for which regression components correspond to
which columns.
Dictionary with keys 'additive' and 'multiplicative' listing the
component names for each mode of seasonality.
seasonal_features = []
prior_scales = []
modes = {'additive': [], 'multiplicative': []}
# Seasonality features #傅里叶变换分解yearly weekly daily等周期信息,在固定的Period(周期)内,输入的X值每个周期是一样的
for name, props in self.seasonalities.items():
features = self.make_seasonality_features(
df['ds'],
props['period'],
props['fourier_order'],
name,
if props['condition_name'] is not None:
features[~df[props['condition_name']]] = 0
seasonal_features.append(features)
prior_scales.extend(
[props['prior_scale']] * features.shape[1])
modes[props['mode']].append(name)
# Holiday features
holidays = self.construct_holiday_dataframe(df['ds'])
if len(holidays) > 0:
features, holiday_priors, holiday_names = (
self.make_holiday_features(df['ds'], holidays)
seasonal_features.append(features)
prior_scales.extend(holiday_priors)
modes[self.seasonality_mode].extend(holiday_names)
# Additional regressors
for name, props in self.extra_regressors.items():
seasonal_features.append(pd.DataFrame(df[name]))
prior_scales.append(props['prior_scale'])
modes[props['mode']].append(name)
# Dummy to prevent empty X 如果什么seasonal feature也没的话,会自己加一个全零的dummy feature
if len(seasonal_features) == 0:
seasonal_features.append(
pd.DataFrame({'zeros': np.zeros(df.shape[0])}))
prior_scales.append(1.)
seasonal_features = pd.concat(seasonal_features, axis=1)
component_cols, modes = self.regressor_column_matrix(
seasonal_features, modes
return seasonal_features, prior_scales, component_cols, modes
此外还有一个set_changepoints函数,实际上就是将训练的时间点等分切割,每一段距离上设一个changepoint。
二、贝叶斯建模
Prophet使用stan语言做贝叶斯建模,即将未知数(如回归系数)视为符合某个分布的随机变量,使用采样方法来预估未知数。Stan代码如下:
// This source code is licensed under the MIT license found in the
// LICENSE file in the root directory of this source tree.
functions {
matrix get_changepoint_matrix(vector t, vector t_change, int T, int S) {
// Assumes t and t_change are sorted.
matrix[T, S] A;
row_vector[S] a_row;
int cp_idx;
// Start with an empty matrix.
A = rep_matrix(0, T, S);
a_row = rep_row_vector(0, S);
cp_idx = 1;
// Fill in each row of A.
for (i in 1:T) {
while ((cp_idx <= S) && (t[i] >= t_change[cp_idx])) {
a_row[cp_idx] = 1;
cp_idx = cp_idx + 1;
A[i] = a_row;
return A;
// Logistic trend functions
vector logistic_gamma(real k, real m, vector delta, vector t_change, int S) {
vector[S] gamma; // adjusted offsets, for piecewise continuity
vector[S + 1] k_s; // actual rate in each segment
real m_pr;
// Compute the rate in each segment
k_s = append_row(k, k + cumulative_sum(delta));
// Piecewise offsets
m_pr = m; // The offset in the previous segment
for (i in 1:S) {
gamma[i] = (t_change[i] - m_pr) * (1 - k_s[i] / k_s[i + 1]);
m_pr = m_pr + gamma[i]; // update for the next segment
return gamma;
vector logistic_trend(
real k,
real m,
vector delta,
vector t,
vector cap,
matrix A,
vector t_change,
int S
vector[S] gamma;
gamma = logistic_gamma(k, m, delta, t_change, S);
return cap .* inv_logit((k + A * delta) .* (t - (m + A * gamma)));
// Linear trend function
vector linear_trend(
real k,
real m,
vector delta,
vector t,
matrix A,
vector t_change
return (k + A * delta) .* t + (m + A * (-t_change .* delta));
// Flat trend function
vector flat_trend(
real m,
int T
return rep_vector(m, T);
data {
int T; // Number of time periods
int<lower=1> K; // Number of regressors
vector[T] t; // Time
vector[T] cap; // Capacities for logistic trend
vector[T] y; // Time series
int S; // Number of changepoints
vector[S] t_change; // Times of trend changepoints
matrix[T,K] X; // Regressors
vector[K] sigmas; // Scale on seasonality prior
real<lower=0> tau; // Scale on changepoints prior
int trend_indicator; // 0 for linear, 1 for logistic, 2 for flat
vector[K] s_a; // Indicator of additive features
vector[K] s_m; // Indicator of multiplicative features
transformed data {
matrix[T, S] A = get_changepoint_matrix(t, t_change, T, S);
matrix[T, K] X_sa = X .* rep_matrix(s_a', T);
matrix[T, K] X_sm = X .* rep_matrix(s_m', T);
parameters {
real k; // Base trend growth rate
real m; // Trend offset
vector[S] delta; // Trend rate adjustments
real<lower=0> sigma_obs; // Observation noise
vector[K] beta; // Regressor coefficients
transformed parameters {
vector[T] trend;
if (trend_indicator == 0) {
trend = linear_trend(k, m, delta, t, A, t_change);
} else if (trend_indicator == 1) {
trend = logistic_trend(k, m, delta, t, cap, A, t_change, S);
} else if (trend_indicator == 2) {
trend = flat_trend(m, T);
model {
//priors
k ~ normal(0, 5);
m ~ normal(0, 5);
delta ~ double_exponential(0, tau);
sigma_obs ~ normal(0, 0.5);
beta ~ normal(0, sigmas);
// Likelihood
y ~ normal_id_glm(
X_sa,
trend .* (1 + X_sm * beta),
beta,
sigma_obs
其中,data为我们输入的数据,transformed_data表示对数据进行的变换,parameters为我们要拟合的模型参数,transformed_parameters表示我们对模型参数进行组合变换后得到的新参数。
Stan中使用的模型为广义线性模型,公式为:
其中,X对应X_sa,表示seasonality中addictive类的分量。
而α对应trend.*(1+X_sm*beta) 注意Stan中的.*表示2个矩阵对应元素相乘,*代表元素相乘,这一点和numpy正好相反。X_sm为seasonality中multiplicative类的分量,beta为我们要拟合的变量,trend是根据我们模型设置的趋势项是linear还是logistics等来决定的,以linear为例,此处trend为
(k + A * delta) .* t + (m + A * (-t_change .* delta)) k,delta和m使我们要拟合的变量,t_change是changepoint对应的标准化后的时间,A为所有t个时间点上,当前时间点是否为changepoint的矩阵,举个简单的例子就是[0,0,0,0]代表当前时间点不是changepoint,[0,0,1,0]代表当前时间点为第三个changepointpoint。
β对应的就是拟合的变量beta;σ对应sigma_obs,代表残差项。使用pymc做拟合,得到python版本的代码:
class prophet_model:
def __init__(self,dat) -> None:
self.dat = dat
#transformed data
self.A = self.get_changepoint_matrix(dat['t'],dat['t_change'],dat['T'],dat['S'])
self.X_sa = dat['X'] * \
np.repeat(dat["s_a"].values,dat["T"]).reshape(len(dat['s_a']),dat['T']).T
self.X_sm = dat['X'] * \
np.repeat(dat["s_m"].values,dat["T"]).reshape(len(dat['s_m']),dat['T']).T
#transformed parameters
def transform_paras(self,k,m,delta):
dat = self.dat
if dat['trend_indicator'] == 0:
trend = self.linear_trend(k,m,delta,dat['t'],self.A,dat['t_change'])
elif dat['trend_indicator'] == 1:
trend = self.logistic_trend(k,m,delta,dat['t'],dat['cap'],self.A,dat['t_change'],dat['S'])
elif dat['trend_indicator'] == 2:
trend = self.flat_trend(m,dat['T'])
return trend
def fit(self):
dat = self.dat
model = pm.Model()
with model:
k = pm.Normal('k',mu=0,sigma=5)
m = pm.Normal('m',mu=0,sigma=5)
delta = pm.Laplace('delta',mu=0,b=dat['tau'],shape=dat['S'])
sigma_obs = pm.HalfNormal('sigma_obs',sigma=0.5)
beta = pm.Normal("beta",0,np.array(dat["sigmas"]))
alpha = (pm.math.dot(self.X_sm,beta)+pm.math.ones_like(pm.math.dot(self.X_sm,beta)))*self.transform_paras(k,m,delta)
mu = alpha + pm.math.dot(self.X_sa,beta)
Y_obs = pm.Normal("obs",observed=dat["y"],mu=mu,sigma=sigma_obs)
map_estimate = pm.find_MAP(model=model,start=stan_init)
return map_estimate,model
def get_changepoint_matrix(self,t,t_change,T,S):
A = np.zeros([T,S])
for i in range(T):
while j<S and t[i]>=t_change[j]:
A[i][j]=1
return A
def logistic_gamma(self,k,m,delta,t_change,S):
# gamma:调整偏移量,以实现分段连续性
# k_s:每段的实际“速率”
k_s = np.cumsum(delta)+k
k_s = np.concatenate([k,k_s])
gamma = np.zeros(S)
m_pr = m
for i in range(S):
gamma[i] = (t_change[i]-m_pr)*(1 - k_s[i] / k_s[i + 1])
m_pr += gamma[i]
return gamma
def linear_trend(self,k,m,delta,t,A,t_change):
return (k+pm.math.dot(A,delta)*t)+(m+pm.math.dot(A,(-t_change*delta)))
def logistic_trend(self,k,m,delta,t,cap,A,t_change,S):
gamma = self.logistic_gamma(k, m, delta, t_change, S)
def inv_logit(x):
return 1/(1+np.exp(-x))
return cap*inv_logit(k+A*delta)*(t-(m+A*gamma))
def flat_trend(self,m,T):
return np.repeat([m],T)
其中stan_init变量为prophet在python中初始化的kinit变量,但实际上按照贝叶斯建模的逻辑,这个初始化的值应该是不影响最终得到的结果的。
Prophet的fit函数如下,为了获取dat参数,我将后面传入stan模型的那部分函数注释了起来。
ef fit(self, df, **kwargs):
"""Fit the Prophet model.
This sets self.params to contain the fitted model parameters. It is a
dictionary parameter names as keys and the following items:
k (Mx1 array): M posterior samples of the initial slope.
m (Mx1 array): The initial intercept.
delta (MxN array): The slope change at each of N changepoints.
beta (MxK matrix): Coefficients for K seasonality features.
sigma_obs (Mx1 array): Noise level.
Note that M=1 if MAP estimation.
Parameters
----------
df: pd.DataFrame containing the history. Must have columns ds (date
type) and y, the time series. If self.growth is 'logistic', then
df must also have a column cap that specifies the capacity at
each ds.
kwargs: Additional arguments passed to the optimizing or sampling
functions in Stan.
Returns
-------
The fitted Prophet object.
if self.history is not None:
raise Exception('Prophet object can only be fit once. '
'Instantiate a new object.')
if ('ds' not in df) or ('y' not in df):
raise ValueError(
'Dataframe must have columns "ds" and "y" with the dates and '
'values respectively.'
history = df[df['y'].notnull()].copy()
if history.shape[0] < 2:
raise ValueError('Dataframe has less than 2 non-NaN rows.')
self.history_dates = pd.to_datetime(pd.Series(df['ds'].unique(), name='ds')).sort_values()
history = self.setup_dataframe(history, initialize_scales=True) #重设index并做标准化
self.history = history
self.set_auto_seasonalities() #此处设置auto了,就代表实际上已经是将默认参数放到模型中,只不过这个函数会挨个判断有没有Daily Weekly Yearly的属性
seasonal_features, prior_scales, component_cols, modes = (
self.make_all_seasonality_features(history))
self.train_component_cols = component_cols
self.component_modes = modes
self.fit_kwargs = deepcopy(kwargs)
self.set_changepoints() #此处的change_points就是在前面changepoint_range范围内,将等距离取n_changepoints个点
trend_indicator = {'linear': 0, 'logistic': 1, 'flat': 2}
dat = {
'T': history.shape[0],
'K': seasonal_features.shape[1],
'S': len(self.changepoints_t),
'y': history['y_scaled'],
't': history['t'],
't_change': self.changepoints_t,
'X': seasonal_features,
'sigmas': prior_scales,
'tau': self.changepoint_prior_scale,
'trend_indicator': trend_indicator[self.growth],
's_a': component_cols['additive_terms'],
's_m': component_cols['multiplicative_terms'],
if self.growth == 'linear':
dat['cap'] = np.zeros(self.history.shape[0])
kinit = self.linear_growth_init(history)
elif self.growth == 'flat':
dat['cap'] = np.zeros(self.history.shape[0])
kinit = self.flat_growth_init(history)
else:
dat['cap'] = history['cap_scaled']
kinit = self.logistic_growth_init(history)
stan_init = {
'k': kinit[0],
'm': kinit[1],
'delta': np.zeros(len(self.changepoints_t)),
'beta': np.zeros(seasonal_features.shape[1]),
'sigma_obs': 1,
return stan_init, dat, kwargs
# if history['y'].min() == history['y'].max() and \
# (self.growth == 'linear' or self.growth == 'flat'):
# self.params = stan_init
# self.params['sigma_obs'] = 1e-9
# for par in self.params:
# self.params[par] = np.array([self.params[par]])
# elif self.mcmc_samples > 0:
# self.params = self.stan_backend.sampling(stan_init, dat, self.mcmc_samples, **kwargs)
# else:
# self.params = self.stan_backend.fit(stan_init, dat, **kwargs)
# self.stan_fit = self.stan_backend.stan_fit
# # If no changepoints were requested, replace delta with 0s
# if len(self.changepoints) == 0:
# # Fold delta into the base rate k
# self.params['k'] = (
# self.params['k'] + self.params['delta'].reshape(-1)
# )
# self.params['delta'] = (np.zeros(self.params['delta'].shape)
# .reshape((-1, 1)))
# return self
prophet在预测时需要使用make_future_dataframe函数来指定预测未来多少天;实际上就是将时间点从预测的时间段延长到未来的那个日期,模型本身的预测必须将他们一并预测出来,无法割裂地只预测未来n天。
模型将季节性因素(包括节假日)和趋势项个因素分别作预测:
(一)、趋势项
此处以linear_growth(线性增长)为例(不知道为什么,我跑logistics增长会卡死,一直跑不出结果出来)。本质上就是根据changepoint将时间线切割成n块,得到一个阶梯形的举证,使用训练好的delta来作为权重矩阵相乘再加k,获得“每个changepoints到changepoints时间段”上的权重。最后再加上偏移量m,得到趋势项的预测。
def piecewise_linear(t, deltas, k, m, changepoint_ts):
"""Evaluate the piecewise linear function.
Parameters
----------
t: np.array of times on which the function is evaluated.
deltas: np.array of rate changes at each changepoint.
k: Float initial rate.
m: Float initial offset.
changepoint_ts: np.array of changepoint times.
Returns
-------
Vector y(t).
deltas_t = (changepoint_ts[None, :] <= t[..., None]) * deltas #[None, :]将(25,)变形为(1,25) t[..., None]将(942,)变形为(942,1) 最终的形状为(942, 25),每行代表当前时间是否“经过了”25个changepoints的时间点;应当是阶梯矩阵,最终将他们乘以deltas
k_t = deltas_t.sum(axis=1) + k
m_t = (deltas_t * -changepoint_ts).sum(axis=1) + m
return k_t * t + m_t
(二)、季节因素
使用前文的make_all_seasonality_features所得出的各个component 0-1分量来筛选beta。对每个分量进行预测。不过要注意的是,再component中,只有"additive_terms"和"multiplicative_terms"这2个汇总的分量会被算入最后的yhat中,尽管某些列由于有汇总多算了几遍,但实际上并结果并不会因此多出。
def predict_seasonal_components(self, df):
"""Predict seasonality components, holidays, and added regressors.
Parameters
----------
df: Prediction dataframe.
Returns
-------
Dataframe with seasonal components.
seasonal_features, _, component_cols, _ = (
self.make_all_seasonality_features(df)
if self.uncertainty_samples:
lower_p = 100 * (1.0 - self.interval_width) / 2
upper_p = 100 * (1.0 + self.interval_width) / 2
X = seasonal_features.values
data = {}
for component in component_cols.columns:
beta_c = self.params['beta'] * component_cols[component].values
comp = np.matmul(X, beta_c.transpose())
if component in self.component_modes['additive']:
comp *= self.y_scale
data[component] = np.nanmean(comp, axis=1)
if self.uncertainty_samples:
data[component + '_lower'] = self.percentile(
comp, lower_p, axis=1,
data[component + '_upper'] = self.percentile(
comp, upper_p, axis=1,
return pd.DataFrame(data)
最终,我们将addictive,multiplicative和trend三者结合,获得最终的预测结果。
def predict(self, df: pd.DataFrame = None, vectorized: bool = True) -> pd.DataFrame:
"""Predict using the prophet model.
Parameters
----------
df: pd.DataFrame with dates for predictions (column ds), and capacity
(column cap) if logistic growth. If not provided, predictions are
made on the history.
vectorized: Whether to use a vectorized method to compute uncertainty intervals. Suggest using
True (the default) for much faster runtimes in most cases,
except when (growth = 'logistic' and mcmc_samples > 0).
Returns
-------
A pd.DataFrame with the forecast components.
if self.history is None:
raise Exception('Model has not been fit.')
if df is None:
df = self.history.copy()
else:
if df.shape[0] == 0:
raise ValueError('Dataframe has no rows.')
df = self.setup_dataframe(df.copy())
df['trend'] = self.predict_trend(df)
seasonal_components = self.predict_seasonal_components(df)
if self.uncertainty_samples:
intervals = self.predict_uncertainty(df, vectorized)
else:
intervals = None
# Drop columns except ds, cap, floor, and trend
cols = ['ds', 'trend']
if 'cap' in df:
cols.append('cap')
if self.logistic_floor:
cols.append('floor')
# Add in forecast components
df2 = pd.concat((df[cols], intervals, seasonal_components), axis=1)
df2['yhat'] = (
df2['trend'] * (1 + df2['multiplicative_terms'])
+ df2['additive_terms']
return df2
四、pymc模型效果实验
此处拿kaggle上的rossmann数据集中的某一家店铺做实验,代码如下:
data = pd.read_pickle("train.pkl")
data = data[["Store","Date","Open","Promo","Sales"]]
sc = StandardScaler()
tmp = data[data.Store == 618]
tmp.Sales = tmp.Sales.replace(0,np.nan)
tmp.Sales = sc.fit_transform(tmp.Sales.values.reshape(-1, 1)).flatten()
tmp.head()
holiday_df = pd.DataFrame({
"holiday":"Promo",
"ds":tmp[tmp.Promo==1].Date,
"upper_window":2,
"lower_window":-2
tmp = tmp.rename({"Date":"ds","Sales":"y"},axis=1)
prophet_test = Prophet(holidays=holiday_df)
df_to_fit = tmp[tmp.ds<=max(tmp.ds)-pd.Timedelta("48 days")]
valid = tmp[tmp.ds>max(tmp.ds)-pd.Timedelta("48 days")]
stan_init, dat, kwargs = prophet_test.fit(df_to_fit)
stan_model = prophet_model(dat)
res_paras,model = stan_model.fit()
#此处params有部分参数需要加一个维度,故而手动赋值
prophet_test.params = {'k': np.array([0.17607271]),
'm': np.array([-0.28650166]),
'delta': np.array([ 3.83468394e-10, 3.83468394e-10, 3.83468394e-10, 3.83468396e-10,
3.83468394e-10, -3.83468394e-10, -3.83468394e-10, -3.83468394e-10,
3.83468394e-10, 3.83468394e-10, 3.83468401e-10, 3.83468396e-10,
3.83468401e-10, 3.83468400e-10, -3.83468399e-10, 3.83468394e-10,
3.83468394e-10, -3.83468393e-10, -3.83468394e-10, 3.83468394e-10,
3.83468399e-10, -3.83468396e-10, 3.83468397e-10, 3.83468396e-10,
-3.83468396e-10]),
'sigma_obs_log__': np.array([-2.00955212]),
'beta': np.array([[ 0.01117073, 0.02496581, -0.04997757, 0.03332093, -0.04325215,
0.02869929, -0.04351403, 0.02107482, -0.0323463 , 0.01525876,
-0.02853991, -0.01302034, -0.02475167, 0.00063693, -0.01806435,
0.00247632, -0.01524688, 0.00710171, -0.00819142, -0.01022585,
0.09467976, -0.06435573, 0.02088479, -0.01316724, -0.02203541,
-0.00759825, 0.17168579, -0.01900267, 0.01997944, 0.08200404,
0.03400996]]),
'sigma_obs': np.array([0.1340487])}
df=future
vectorized=True
if prophet_test.history is None:
raise Exception('Model has not been fit.')
if df is None:
df = prophet_test.history.copy()
else:
if df.shape[0] == 0:
raise ValueError('Dataframe has no rows.')
df = prophet_test.setup_dataframe(df.copy())
df['trend'] = prophet_test.predict_trend(df)
seasonal_components = prophet_test.predict_seasonal_components(df)
if prophet_test.uncertainty_samples:
intervals = prophet_test.predict_uncertainty(df, vectorized)
else:
intervals = None
# Drop columns except ds, cap, floor, and trend
cols = ['ds', 'trend']
if 'cap' in df:
cols.append('cap')
if prophet_test.logistic_floor:
cols.append('floor')
# Add in forecast components
df2 = pd.concat((df[cols], intervals, seasonal_components), axis=1)
df2['yhat'] = (
df2['trend'] * (1 + df2['multiplicative_terms'])
+ df2['additive_terms']
tmp = tmp.sort_values("ds")
tmp.index = tmp.ds
tmp_y = tmp[~np.isnan(tmp["y"])]
y_predict = df2.loc[:,["ds","yhat"]]
y_predict.index = y_predict.ds
tmp_y.drop("ds",axis=1,inplace=True)
y_predict.drop("ds",axis=1,inplace=True)
res = tmp_y.merge(y_predict,how="left",on="ds")
res.y = sc.inverse_transform(res.y.values.reshape(-1,1)).flatten()
res.yhat = sc.inverse_transform(res.yhat.values.reshape(-1,1)).flatten()
valid_res = res[res.index>=pd.to_datetime("2015-06-14")]
print(np.sqrt(np.mean(((valid_res.yhat-valid_res.y)/valid_res.y)**2)))
其结果(RMSPE)为
而在prophet原生上效果则好很多:
可能是由于Stan与pymc的算法实现有所差异或者是prophet在版本更新时与我现在解读的代码有部分差异。
Prophet 的算法实现
在时间序列分析领域,有一种常见的分析方法叫做时间序列的分解 (Decomposition of Time Series),它把时间序列 分成几个部分,分别是季节项 ,趋势项 ,剩余项 。也就是 说对所有的 ,都有
除了加法的形式,还有乘法的形式,也就是:
以上式子等价于 。所以,有的时候在预测模型的时候,会先取 对数,然后再进行时间序列的分解,就能得到乘法的形式。在 fbprophet 算法中,作者们基于这 种方法进行了必要的改进和优化。一般来说,在实际生活和生产环节中,除了季节项,趋势项,剩余项之外,通常还有节假日的效 应。所以,在 prophet 算法里面,作者同时考虑了以上四项,也就是:
其中 表示趋势项,它表示时间序列在非周期上面的变化趋势; 表示周期项,或者称为 季节项,一般来说是以周或者年为单位; 表示节假日项,表示在当天是否存在节假日; 表 示误差项或者称为剩余项。Prophet 算法就是通过拟合这几项,然后最后把它们累加起来就得到了 时间序列的预测值。
Python PyMC库是一个强大而灵活的概率编程库,用于贝叶斯统计建模和蒙特卡罗采样。通过本文的详细介绍和示例代码,可以了解PyMC库的基本用法和高级功能,并在实际项目中应用该库来进行贝叶斯推断和概率建模。PyMC库的出现为数据科学和机器学习领域的应用提供了强大的支持。
时序预测工具库(Prophet)一、Prophet 简介二、Prophet 适用场景三、Prophet 算法的输入输出四、Prophet 算法原理六、代码6.1 依赖安装6.2 预测demo6.3 效果图七、参考资料八、官方链接:九、案例链接:
项目地址:
https://aistudio.baidu.com/aistudio/projectdetail/525311?channelType=0&channel=0
参考内容:
时间序列模型Prophet使用详细讲解
初识Prophet模型(一)--
Prophet是由Facebook开发的时间序列预测工具,专为处理具有**趋势、季节性和节假日效应**的数据而设计。它能够捕捉数据的**整体趋势、考虑周期性模式,同时允许用户指定特殊日期的影响**。Prophet简单易用,具有自动检测变化点的功能,同时提供可解释的结果。无论是销售数据、股价还是其他时间序列数据,都可以用prophet进行预测,但更多的是通过prophet提取特征。
论文笔记:Forecasting at Scale(Prophet)_UQI-LIUWJ的博客-CSDN博客
Prophet 是一种基于加法模型预测时间序列数据的程序,其中非线性趋势、季节性以及假日效应相匹配。
它最适用于具有强烈季节性和有几个季节历史数据的时间序列。
Prophet 对缺失数据和趋势变化具有鲁棒性,并且通常可以很好地处理异常值。
总体而言,Prophet模型通过这些组件的组合来建模时间序列数据中的趋势、季节性、假期效应和噪声。"Prophet" 指的是由 Facebook 开发的一种用于时间序列分析和预测的工具。Prophet 在 R 和 Python 中都有实现,由于其能够以极小的工作量生成准确且易于解释的预测,因此在各个行业中广受欢迎。要使用 Prophet,通常需要提供一个包含两列的时间序列数据集:'ds'(日期)和 'y'(要预测的值)。可调参数:可以调整各种参数以定制模型的行为,例如季节性组件的强度和趋势的灵活性。
Prophet是一个由Facebook开发的开源工具,用于时间序列预测。这个工具特别适合于具有强季节性影响和多个历史数据季节的业务时间序列数据。Prophet的主要思想是将数据分解为如下三个部分:趋势、季节性、节假日和特殊事件。这个模型非常适合于处理具有强烈季节性和趋势变化的业务时间序列数据(这里为什么适合的是业务数据呢是因为它考虑了节假日等特殊事件,同时其面对数据中的缺失值和异常值时也能保持其性能)。Prophet通过这种方式,可以有效地预测未来的趋势和模式。需要注意的是。
Prophet是Facebook开发的开源时间序列预测工具,用于处理时间序列数据的建模和预测。它建立在统计模型之上,适用于多种时间序列预测问题,具有易用性和灵活性。能够处理缺失值和异常值支持对节假日和季节性的建模可以灵活地添加自定义的季节性成分自动检测变化点提供了直观的可视化工具这个简短的教程为您提供了使用Prophet进行时间序列预测的基本步骤和一些重要的概念。您可以通过阅读Prophet官方文档和其他在线资源来进一步深入学习和了解更多细节。
最近又接到一个预测项目需求,主要是预测每天投资用户会投资不同产品多少金额,属于每天即时预测,需要拿最近一年的数据做测试集,来预测每天不同期限产品分别被投资多少金额,然后通过这些金额每天找借款端匹配借款需求,借款端运营通过资金端需求来动态调整营销活动,通过资金需求多少来有效运营借款需求,形成与资金端的良性互动,节约闲置资金成本。
就这样一个需求,如何实现?我首先想到通过业务经验
