看溢价率水平的话，上周小盘转债基本回到了与大盘转债的同等的水平 —— 我们跟踪的百元溢价率，在上周二者都达到了 12.2% 附近，区别是大盘转债是向下移动而小盘转债是从 2 月反弹至今。投资者可能知道这意味着什么，毕竟 2018 年之后，如果排除 “ 妖债 ” 的话，小盘转债的溢价率就少有在大盘之上的时候。这样来看，市场似乎很快淡化了此前 11 月时对小盘转债的悲观 —— 比如信用风险。而在我们来看，转债并未发生过违约，但发生过 “ 暂停交易 ” 。此前 A 股退市新规的发布，也让这个风险变得比此前更显性化、更实际一些 —— 无论我们当下是否推荐投资者去更多参与小转债，此时都有必要花时间去刻画这个风险。

简单来说，“1元退市”和“3亿市值退市”是两条红线。 根据沪深交易所规定，股票连续20日股价低于1元或低于3亿元则面临退市压力，而此时对应的转债也“应当终止上市”。于是不难刻画：

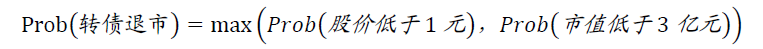
实现起来当然不难，我们要考虑一个实际问题： 转债数量众多，特别是如果考虑把这个数据加入到策略中的话，我们要用足够快、也足够稳定的方法。这要求算法尽可能简单、可以被矢量化，也尽可能少用到估计出来的参数——这基本决定了模拟法被排除在外。我们用一个很简单的模型：假定为S 0 当前股价，S T 为期末，MV 0 为当前市值，MV T 为期末市值,则：

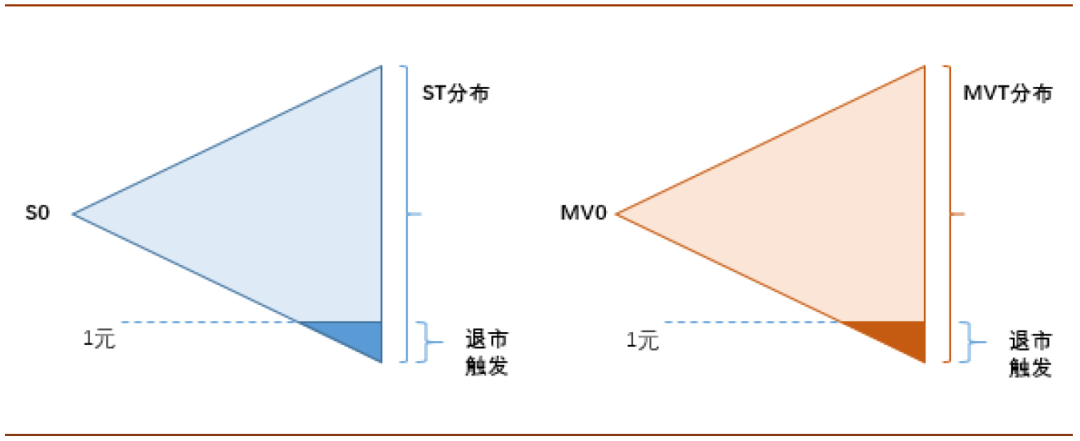
资料来源：中金公司研究部

我们没有加入“飘移项”，其中的vol为股价波动率，用3年的周度数据算出，h为股价周线的hurst指数，在0~1之间，大体上它意味着股价的趋势性，Black-Scholes模型中用到的几何布朗运动实际上是h=0.5时的特例，而股价多数会略高于0.5，体现更强的趋势性，当然也有部分转债正股的h低于0.5，体现均值回复属性。

实现过程上，我们首先要取股价、市值数据，为了得到vol和h，我们还需要过去3年的股价周度走势。 这些都不难，转债投资者仅注意这里需要一个转债代码与正股代码转换的问题即可。此外，计算波动率时停牌时期不予考虑，为简便，我们把周涨跌幅严格为0的时间点直接设None。程序逻辑如下：

def getUnderlyingCodeTable(codes):
    '''得到转债与正股代码转换表，仅'''
    if not w.isconnected(): w.start()
    _, df = w.wss(','.join(codes), "underlyingcode", usedf=True)
    return df
    
def getPtm(df, date):
    _, rt = w.wss(','.join(df.index), "Ptm", "tradedate=" + pd.to_datetime(date).strftime("%Y%m%"), usedf=True)
    df["Ptm"] = rt["Ptm"]
    return df

def getStockAndMV(codes, date):
    '''这里得到当前股价，codes为转债代码列表，date为日期，任意格式即可'''
    date = pd.to_datetime(date).strftime("%Y%m%d")
    
    df = getUnderlyingCodeTable(codes)
    stocks = list(set(df.UNDERLYINGCODE))
    if not w.isconnected(): w.start()
        
    _, dfRaw = w.wss(','.join(stocks), "close,mkt_cap_ard", \
    "tradedate=" + date, usedf=True)

    df = df.merge(dfRaw, left_on="UNDERLYINGCODE", right_index=True)
    
    return df

def get3YearsWeeklyReturnDF(stocks, date):
    '''取正股的3年周度涨跌幅'''
    if not w.isconnected(): w.start()
    qstart = w.tdaysoffset(-750, date).Data[0][0].strftime('%Y%m%d')
    
    _, dfRaw = w.wsd(",".join(stocks), "PCT_CHG", qstart, date, "period=w", usedf=True) 
    
    return dfRaw.applymap(lambda x: None if x == 0 else x)




    

资料来源：中金公司研究部

下面我们要计算股价波动率和hurst值。 这里波动率的计算十分简单，而后者为分形几何中常见的概念，如无相关基础可先行跳过，转债标的均值为0.58，分化也并不太大。

def hurst2(srs):

    if not isinstance(srs, pd.Series): srs = pd.Series(srs)
    
    lstRS = []
    lstN = range(3, len(srs)//2)
    for n in lstN:
        collects = [srs.iloc[i: (i+n)] for i 
in range(0, len(srs), n)]
        _list = []
        for _s in collects:
            X = (_s - _s.mean()).cumsum()

            RS = (X.max() - X.min()) / pd.np.std(_s)
            if not pd.isna(RS): _list.append(RS)

        lstRS.append(pd.np.mean(_list))

    return np.polyfit(pd.np.log(lstN), pd.np.log(lstRS),1)[0]

资料来源：中金公司研究部

在上述参数齐全的情况下，按照前述公式，转债退市的概率反而最容易计算，如下：

def beDelisted(s, mv, vol, t, h=0.5):
    p1 = stats.norm.cdf((np.log(1) - np.log(s)) / (vol * (t ** h)))
    p2 = stats.norm.cdf((np.log(3) - np.log(mv)) / (vol * (t ** h)))
    
    return max((p1,p2))

资料来源：中金公司研究部

最后是将上述内容整合到一起，这里由于只是计算一列数据，没必要再建立class变量。如下方式即可得到最后结果：

def getPctBeDelisted3(codes, odate):

    df = getStockAndMV(codes,date)
    df = getPtm(df)
    
    stocks = list(set(df["UNDERLYINGCODE"]))
    dfWkPct = get3YearsWeeklyReturnDF(stocks, date)
    dfRiskPara = pd.DataFrame(index=stocks)
    
    dfRiskPara["vol"] = dfWkPct.std()/ 100.0
    dfRiskPara["h"] = dfWkPct.apply(hurst2)
    
    df = df.merge(dfRiskPara, left_on="UNDERLYINGCODE"
, right_index=True)
    
    df["Pct2BeDelisted"] = None

    for code in df.index:

        t = min((df.loc[code, "Ptm"] * 50,150))
        vol = df.loc[code, "vol"]
        h = df.loc[code, "h"]
        
        df.loc[code, "Pct2BeDelisted"] = beDelisted(df.CLOSE[code], df.MKT_CAP_ARD[code]/100000000.0, vol, t, h)
        
    return df




    

资料来源：中金公司研究部

最后，几个投资者可能会问到的问题：

1、这个数据如何关联到实战？ 显然，极端场景下的风险防范是低估值类策略的弱点——但无论是纯粹的“双低”还是我们此前的easy ball，都是比较容易改进的。比如加入这个因子，作为负面剔除项。在此我们不具体展示名单，但也容易看到，此前在低估值状态下依然出现较大回撤风险甚至跌破债底的品种，与该数据的高低，有比较明显的关联性。

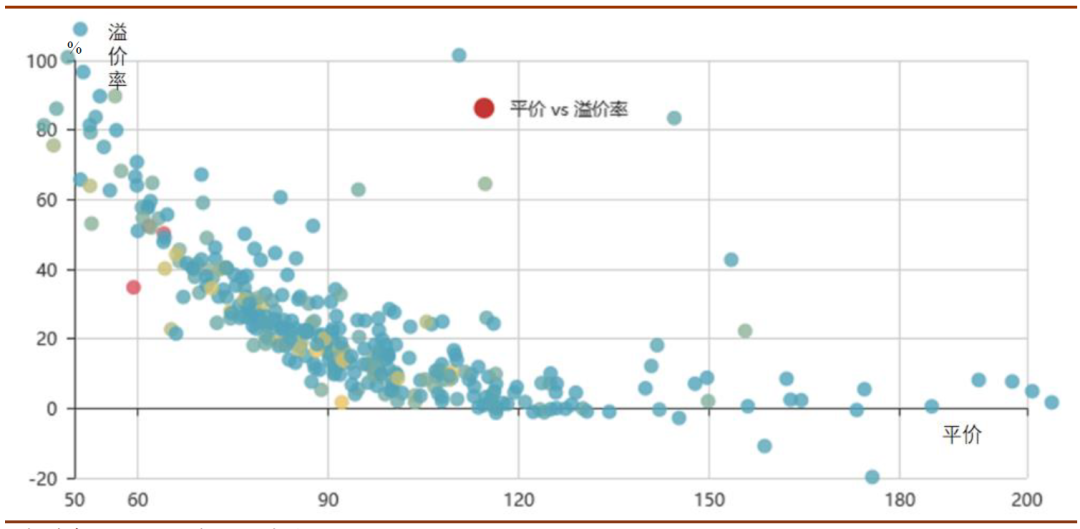
2、对于面临“1元退市”风险的品种，是否合股可以破解？ ——理论上是，但目前暂无先例，市场也不会形成这样的预期。 且通过这样的方法规避退市，也容易产生各类问题（参考港股市），与注册制的精神有悖，我们不建议考虑这种可能性。

3、上述处理会高估次新股的风险：次新股由于并没有太长的股价历史，且其上市初期波动很大，夸大了其波动值和趋势项，参考意义比较小。我们实际的做法是对次新股先通过市值、交易量、股价表现等，找到与其最为相似的5个标的，然后再取这些标的的均值。但这里展开可能会影响理解，我们在上文暂忽略这个问题。