本文分享一个“万物皆可盘”的NLP对抗训练实现,只需要四行代码即可调用。盘他。
最近,微软的FreeLB-Roberta [1] 靠着对抗训练 (Adversarial Training) 在GLUE榜上超越了Facebook原生的Roberta,追一科技也用到了这个方法仅凭单模型 [2] 就在CoQA榜单中超过了人类,似乎“对抗训练”一下子变成了NLP任务的一把利器。刚好笔者最近也在看这方面的内容,所以开一篇博客,讲一下。
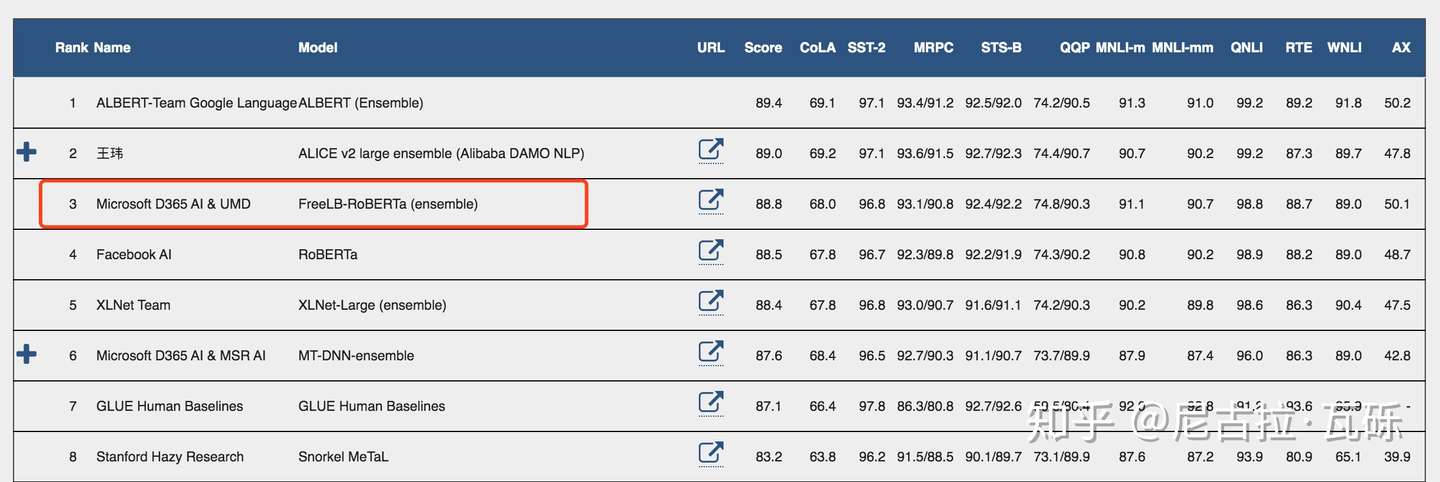 GLUE Leaderboard
GLUE Leaderboard
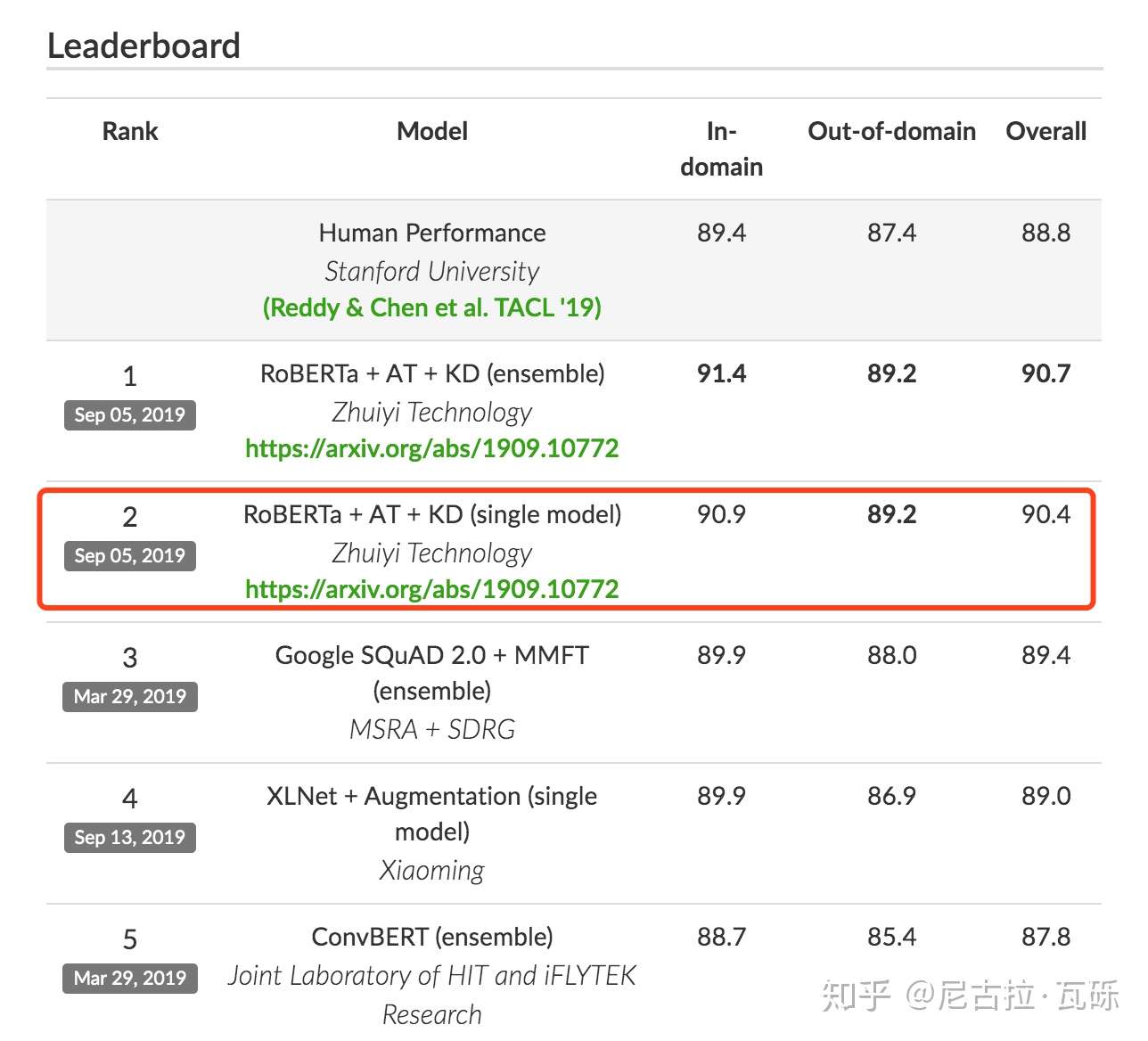 CoQA Leaderboard
CoQA Leaderboard
提到“对抗”,相信大多数人的第一反应都是CV中的对抗生成网络 (GAN),殊不知,其实对抗也可以作为一种防御机制,并且经过简单的修改,便能用在NLP任务上,提高模型的泛化能力。关键是,对抗训练可以写成一个插件的形式,用几行代码就可以在训练中自由地调用,简单有效,使用成本低。不过网上的大多数博客对于NLP中的对抗训练都介绍得比较零散且无代码实现,笔者在这篇博客中,对NLP任务中的对抗训练做了一个简单的综述,并提供了插件形式的PyTorch实现。
本文专注于NLP对抗训练的介绍,对对抗攻击基础感兴趣的读者,可以看这几篇博客及论文 [3] [4] [5],这里就不赘述了。不想要理解理论细节的读者也可以直接看最后的代码实现。
1. 对抗样本
我们常常会听到“对抗样本”、“对抗攻击”、“对抗训练”等等这些令人头秃的概念,为了让大家对“对抗”有个更清晰的认识,我们先把这些概念捋捋清楚。
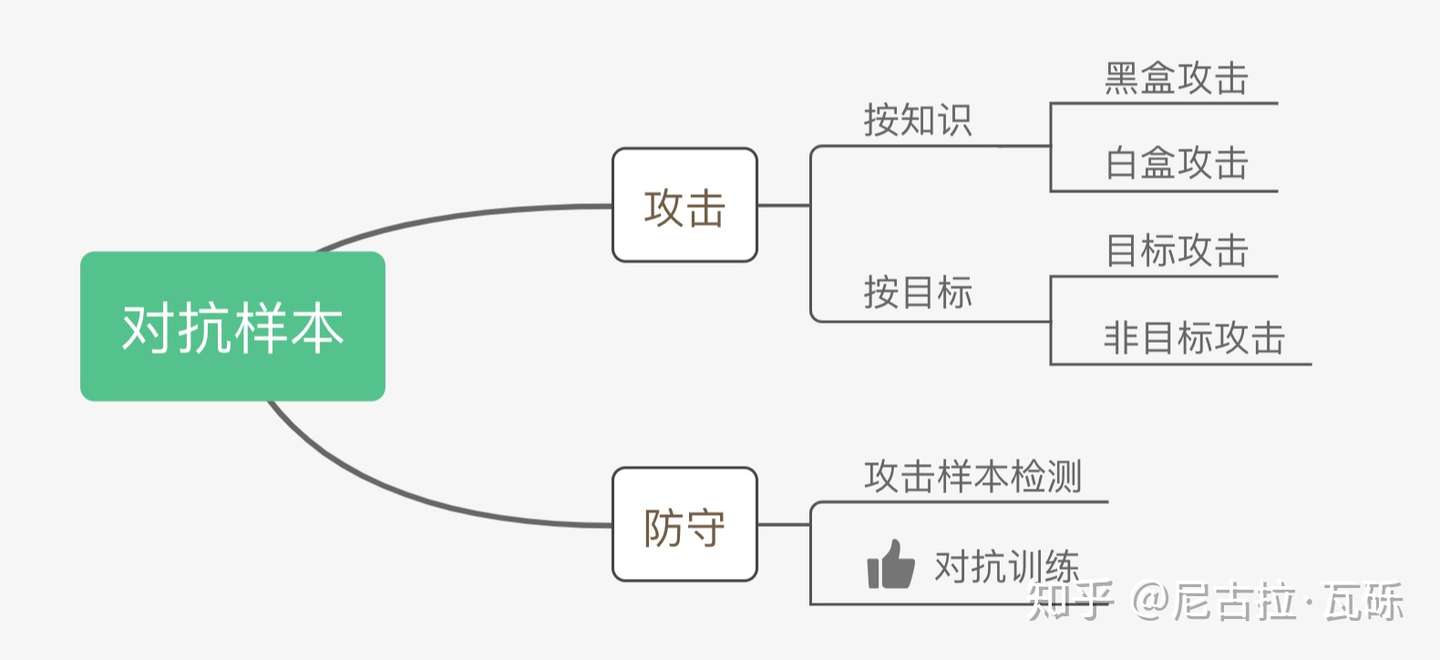 Taxonomy
Taxonomy
Szegedy在14年的ICLR中 [6] 提出了对抗样本这个概念。如上图,对抗样本可以用来攻击和防御,而对抗训练其实是“对抗”家族中防御的一种方式,其基本的原理呢,就是通过添加扰动构造一些对抗样本,放给模型去训练,以攻为守,提高模型在遇到对抗样本时的鲁棒性,同时一定程度也能提高模型的表现和泛化能力。
那么,什么样的样本才是好的对抗样本呢?对抗样本一般需要具有两个特点:
相对于原始输入,所添加的扰动是微小的;
能使模型犯错。
下面是一个对抗样本的例子,决定就是你啦,胖达:
 一只胖达加了点扰动就被识别成了长臂猿
一只胖达加了点扰动就被识别成了长臂猿
2. 对抗训练的基本概念
GAN之父Ian Goodfellow在15年的ICLR中 [7] 第一次提出了对抗训练这个概念,简而言之,就是在原始输入样本
![[公式]](https://www.zhihu.com/equation?tex=x) 上加一个扰动
上加一个扰动
![[公式]](https://www.zhihu.com/equation?tex=+r_%7Badv%7D) ,得到对抗样本后,用其进行训练。也就是说,问题可以被抽象成这么一个模型:
,得到对抗样本后,用其进行训练。也就是说,问题可以被抽象成这么一个模型:
其中,
![[公式]](https://www.zhihu.com/equation?tex=y) 为gold label,
为gold label,
![[公式]](https://www.zhihu.com/equation?tex=%5Ctheta) 为模型参数。那扰动要如何计算呢?Goodfellow认为,神经网络由于其线性的特点,很容易受到线性扰动的攻击。
为模型参数。那扰动要如何计算呢?Goodfellow认为,神经网络由于其线性的特点,很容易受到线性扰动的攻击。
This linear behavior suggests that cheap, analytical perturbations of a linear model should also damage neural networks.
于是,他提出了 Fast Gradient Sign Method (FGSM) ,来计算输入样本的扰动。扰动可以被定义为:
其中,
![[公式]](https://www.zhihu.com/equation?tex=%5Ctext%7Bsgn%7D) 为符号函数,
为符号函数,
![[公式]](https://www.zhihu.com/equation?tex=L) 为损失函数。Goodfellow发现,令
为损失函数。Goodfellow发现,令
![[公式]](https://www.zhihu.com/equation?tex=%5Cepsilon%3D0.25) ,用这个扰动能给一个单层分类器造成99.9%的错误率。看似这个扰动的发现有点拍脑门,但是仔细想想,其实这个扰动计算的思想可以理解为:将输入样本向着损失上升的方向再进一步,得到的对抗样本就能造成更大的损失,提高模型的错误率。回想我们上一节提到的对抗样本的两个要求,FGSM刚好可以完美地解决。
,用这个扰动能给一个单层分类器造成99.9%的错误率。看似这个扰动的发现有点拍脑门,但是仔细想想,其实这个扰动计算的思想可以理解为:将输入样本向着损失上升的方向再进一步,得到的对抗样本就能造成更大的损失,提高模型的错误率。回想我们上一节提到的对抗样本的两个要求,FGSM刚好可以完美地解决。
在 [7] 中,Goodfellow还总结了对抗训练的两个作用:
提高模型应对恶意对抗样本时的鲁棒性;
作为一种regularization,减少overfitting,提高泛化能力。
3. Min-Max 公式
在 [7] 中,对抗训练的理论部分被阐述得还是比较intuitive,Madry在2018年的ICLR中 [8]总结了之前的工作,并从优化的视角,将问题重新定义成了一个找鞍点的问题,也就是大名鼎鼎的Min-Max公式:
该公式分为两个部分,一个是内部损失函数的最大化,一个是外部经验风险的最小化。
内部max是为了找到worst-case的扰动,也就是攻击,其中,
![[公式]](https://www.zhihu.com/equation?tex=L) 为损失函数,
为损失函数,
![[公式]](https://www.zhihu.com/equation?tex=%5Cmathcal%7BS%7D) 为扰动的范围空间。
外部min是为了基于该攻击方式,找到最鲁棒的模型参数,也就是防御,其中
为扰动的范围空间。
外部min是为了基于该攻击方式,找到最鲁棒的模型参数,也就是防御,其中
![[公式]](https://www.zhihu.com/equation?tex=%5Cmathcal%7BD%7D) 是输入样本的分布。
是输入样本的分布。
Madry认为,这个公式简单清晰地定义了对抗样本攻防“矛与盾”的两个问题:如何构造足够强的对抗样本?以及,如何使模型变得刀枪不入?剩下的,就是如何求解的问题了。
4. 从 CV 到 NLP
以上提到的一些工作都还是停留在CV领域的,那么问题来了,可否将对抗训练迁移到NLP上呢?答案是肯定的,但是,我们得考虑这么几个问题:
首先,CV任务的输入是连续的RGB的值,而NLP问题中,输入是离散的单词序列,一般以one-hot vector的形式呈现,如果直接在raw text上进行扰动,那么扰动的大小和方向可能都没什么意义。Goodfellow在17年的ICLR中 [9] 提出了可以在连续的embedding上做扰动:
Because the set of high-dimensional one-hot vectors does not admit infinitesimal perturbation, we define the perturbation on continuous word embeddings instead of discrete word inputs.
乍一思考,觉得这个解决方案似乎特别完美。然而,对比图像领域中直接在原始输入加扰动的做法,在embedding上加扰动会带来这么一个问题:这个被构造出来的“对抗样本”并不能map到某个单词,因此,反过来在inference的时候,对手也没有办法通过修改原始输入得到这样的对抗样本。我们在上面提到,对抗训练有两个作用,一是提高模型对恶意攻击的鲁棒性,二是提高模型的泛化能力。在CV任务,根据经验性的结论,对抗训练往往会使得模型在非对抗样本上的表现变差,然而神奇的是,在NLP任务中,模型的泛化能力反而变强了,如[1]中所述:
While adversarial training boosts the robustness, it is widely accepted by computer vision researchers that it is at odds with generalization, with classification accuracy on non-corrupted images dropping as much as 10% on CIFAR-10, and 15% on Imagenet (Madry et al., 2018; Xie et al., 2019). Surprisingly, people observe the opposite result for language models (Miyato et al., 2017; Cheng et al., 2019), showing that adversarial training can improve both generalization and robustness.
因此,在NLP任务中,对抗训练的角色不再是为了防御基于梯度的恶意攻击,反而更多的是作为一种regularization,提高模型的泛化能力。
有了这些“思想准备”,我们来看看NLP对抗训练的常用的几个方法和具体实现吧。
5. NLP中的两种对抗训练 + PyTorch实现
a. Fast Gradient Method(FGM)
上面我们提到,Goodfellow在15年的ICLR [7] 中提出了Fast Gradient Sign Method(FGSM),随后,在17年的ICLR [9]中,Goodfellow对FGSM中计算扰动的部分做了一点简单的修改。假设输入的文本序列的embedding vectors
![[公式]](https://www.zhihu.com/equation?tex=%5Bv_1%2C+v_2%2C+...%2C+v_T%5D) 为
为
![[公式]](https://www.zhihu.com/equation?tex=x) ,embedding的扰动为:
,embedding的扰动为:
实际上就是取消了符号函数,用二范式做了一个scale,需要注意的是:这里的norm计算的是,每个样本的输入序列中出现过的词组成的矩阵的梯度norm。原作者提供了一个TensorFlow的实现 [10],在他的实现中,公式里的
![[公式]](https://www.zhihu.com/equation?tex=x) 是embedding后的中间结果(batch_size, timesteps, hidden_dim),对其梯度
是embedding后的中间结果(batch_size, timesteps, hidden_dim),对其梯度
![[公式]](https://www.zhihu.com/equation?tex=g) 的后面两维计算norm,得到的是一个(batch_size, 1, 1)的向量
的后面两维计算norm,得到的是一个(batch_size, 1, 1)的向量
![[公式]](https://www.zhihu.com/equation?tex=%7C%7Cg%7C%7C_2) 。为了实现插件式的调用,笔者将一个batch抽象成一个样本,一个batch统一用一个norm,由于本来norm也只是一个scale的作用,影响不大。笔者的实现如下:
。为了实现插件式的调用,笔者将一个batch抽象成一个样本,一个batch统一用一个norm,由于本来norm也只是一个scale的作用,影响不大。笔者的实现如下:
import torch
class FGM():
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
需要使用对抗训练的时候,只需要添加五行代码:
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
PyTorch为了节约内存,在backward的时候并不保存中间变量的梯度。因此,如果需要完全照搬原作的实现,需要用
register_hook
接口[11]将embedding后的中间变量的梯度保存成全局变量,norm后面两维,计算出扰动后,在对抗训练forward时传入扰动,累加到embedding后的中间变量上,得到新的loss,再进行梯度下降。不过这样实现就与我们追求插件式简单好用的初衷相悖,这里就不赘述了,感兴趣的读者可以自行实现。
b. Projected Gradient Descent(PGD)
内部max的过程,本质上是一个非凹的约束优化问题,FGM解决的思路其实就是梯度上升,那么FGM简单粗暴的“一步到位”,是不是有可能并不能走到约束内的最优点呢?当然是有可能的。于是,一个很intuitive的改进诞生了:Madry在18年的ICLR中[8],提出了用Projected Gradient Descent(PGD)的方法,简单的说,就是“小步走,多走几步”,如果走出了扰动半径为
![[公式]](https://www.zhihu.com/equation?tex=%5Cepsilon) 的空间,就映射回“球面”上,以保证扰动不要过大:
的空间,就映射回“球面”上,以保证扰动不要过大:
其中
![[公式]](https://www.zhihu.com/equation?tex=%5Cmathcal%7BS%7D%3D%7Br%5Cin%5Cmathbb%7BR%7D%5Ed%3A%7C%7Cr%7C%7C_2+%5Cleq+%5Cepsilon%7D) 为扰动的约束空间,
为扰动的约束空间,
![[公式]](https://www.zhihu.com/equation?tex=%5Calpha) 为小步的步长。
为小步的步长。
import torch
class PGD():
def __init__(self, model):
self.model = model
self.emb_backup = {}
self.grad_backup = {}
def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
 GLUE Leaderboard
GLUE Leaderboard
 CoQA Leaderboard
CoQA Leaderboard
 Taxonomy
Taxonomy
 一只胖达加了点扰动就被识别成了长臂猿
一只胖达加了点扰动就被识别成了长臂猿