在一个指定位置的圆内随机取若干个坐标点,num为数量,radius为圆的半径,(centerx, centery)为圆心坐标。
方法一:根据条件判断的随机点产生方法
import random
import matplotlib.pyplot as plt
def getRandomPointInCircle(num, radius, centerx, centery):
samplePoint = []
for i in range(num):
while True:
x = random.uniform(-radius, radius)
y = random.uniform(-radius, radius)
if (x ** 2) + (y ** 2) <= (radius ** 2):
samplePoint.append((int(x) + centerx, int(y) + centery))
break
plt.plot(x + centerx, y + centery, '*', color="blue")
return samplePoint
if __name__ == "__main__":
num = 1000
radius = 100
centerx,centery = 20, 20
samp = getRandomPointInCircle(num, radius, centerx, centery)
print("sample point" , samp)
plt.legend()
plt.show()
方法二:极坐标产生随机点
import random
import matplotlib.pyplot as plt
def getRandomPointInCircle(num, radius, centerx, centery):
samplePoint = []
for i in range(num):
theta = random.random() * 2 * np.pi
r = random.uniform(0, radius ** 2)
x = math.cos(theta) * (r ** 0.5) + centerx
y = math.sin(theta) * (r ** 0.5) + centery
samplePoint.append((int(x), int(y)))
plt.plot(x, y, '*', color="blue")
return samplePoint
if __name__ == "__main__":
num = 1000
radius = 100
centerx,centery = 20, 20
samp = getRandomPointInCircle(num, radius, centerx, centery)
print("sample point" , samp)
plt.legend()
plt.show()
显示效果
显示如下:
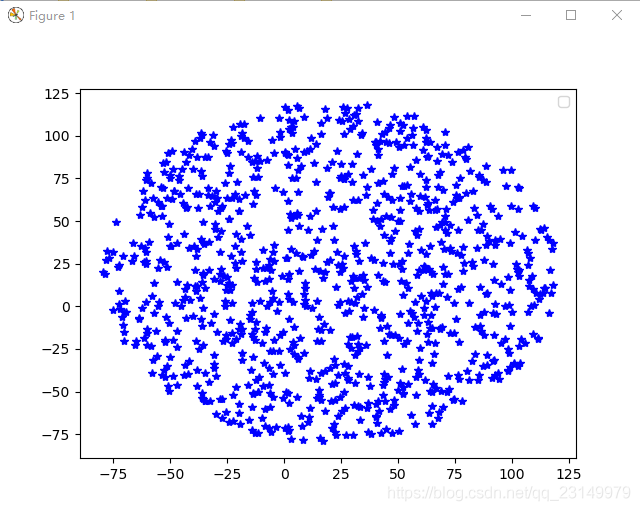
import randomimport matplotlib.pyplot as pltdef getRandomPointInCircle(num, radius, centerx, centery): samplePoint = [] for i in range(num): while True: x = random.unif...
处理数据集的过程中用到了mask 但是源数据集中只给了mask顶点的坐标值,那么在python中怎么实现生成只有0、1表示的mask区域呢?
主要借鉴cv2中的方法:
(我使用的数据情况是将顶点坐标分别存储在roi.mat中的x和y元素)
matfn = 'roi.mat'
data = sio.loadmat(matfn)
x_cor = data['x']
y_cor = data['y']
im = np.zeros(图像对应尺寸, dtype="uint8")
cor_xy = np.hstack((x_cor, y_cor))
cv2.polylines(im, np.int32(
这篇文章主要介绍了python 五子棋如何获得鼠标点击坐标,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下
点坐标的取自:
from tkinter import *
root=Tk()
#创建一个框架,在这个框架中响应事件
frame=Frame(root,width=200,height=200)
def callBackLeft(event):
print("相对于应用程序左上角的位置,左键点击的位置是",event.x,event.y)
print("相对于屏幕左上角的位置,左键点击的位置是",event.x_root,eve
可以使用 Python 库 Matplotlib 中的 pyplot.scatter() 函数来画圆。具体实现方法是,首先用参数 np.linspace(0, 2*np.pi, num_points) 生成一组圆上的点的极角,然后对于每个极角,计算对应的 x, y 坐标并调用 scatter() 函数画点。示例代码如下:
import matplotlib.pyplot as plt
import...
给定圆的半径和圆心的位置,实现函数 randPoint ,在圆中产生均匀随机点。实现 Solution 类:Solution(double radius, double x_center, double y_center) 用圆的半径 radius 和圆心的位置 (x_center, y_center) 初始化对象
randPoint() 返回圆内的一个随机点。圆周上的一点被认为在圆内。答案作为数组返回 [x, y] 。示例 1:提示:0 < radius ...
圆的半径和圆心的 x、y 坐标将作为参数传递给类的构造函数。
圆周上的点也认为是在圆中。
randPoint 返回一个包含随机点的x坐标和y坐标的大小为2的数组。
示例 1:
[“Solution”,“randPoint”,“randPoint”,“randPoint”]
[[1,0,0],[],[],[]]
输出: [null,[-0.7
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], tar.
圆盘内的均匀采样问题,是一个很有意思,也很常被考到的问题。在一个圆形内,均匀采点,怎么保证均匀且随机?
有三种方法:1、正方形采样;2、极坐标采样(错误!);3、圆盘采样
一、正方形采样(Reject Method)
最容易想到的方法就是在正方形内采样,比如要在圆心为原点,半径为1的圆内均匀采样,可以在 x 从 [-1, 1],y 从 -[-1, 1] 的正方形内均匀采样,然后把不在圆...
# base_lat:维度基准点,
# radius:距离基准点的半径
def generate_random_gps(base_log=None, base_lat=None, radius=None):
radius_in_degrees = radius / 111300
u = float(random.uniform(0.0, 1.0))
v = float(random
# 计算矩形的长和宽
width = sorted_coords[3][0] - sorted_coords[0][0]
height = sorted_coords[2][1] - sorted_coords[0][1]
# 随机生成一个点的 x 和 y 坐标
x = random.uniform(sorted_coords[0][0], sorted_coords[3][0])
y = random.uniform(sorted_coords[0][1], sorted_coords[2][1])
# 判断该点是否在矩形内部
if (sorted_coords[1][0] - sorted_coords[0][0]) * (y - sorted_coords[0][1]) - (x - sorted_coords[0][0]) * (sorted_coords[1][1] - sorted_coords[0][1]) >= 0 and \
(sorted_coords[3][0] - sorted_coords[0][0]) * (y - sorted_coords[0][1]) - (x - sorted_coords[0][0]) * (sorted_coords[3][1] - sorted_coords[0][1]) >= 0 and \
(sorted_coords[3][0] - sorted_coords[2][0]) * (y - sorted_coords[2][1]) - (x - sorted_coords[2][0]) * (sorted_coords[3][1] - sorted_coords[2][1]) >= 0 and \
(sorted_coords[1][0] - sorted_coords[2][0]) * (y - sorted_coords[2][1]) - (x - sorted_coords[2][0]) * (sorted_coords[1][1] - sorted_coords[2][1]) >= 0:
print(f"随机生成的点 ({x}, {y}) 在矩形内部")
else:
print(f"随机生成的点 ({x}, {y}) 在矩形外部")
该代码首先将四个坐标进行排序,并计算矩形的长和宽。然后随机生成一个点的 x 和 y 坐标,并判断该点是否在矩形内部。判断的方法是利用向量叉积的性质,判断该点是否在四条边的同侧。如果该点在矩形内部,则输出“随机生成的点在矩形内部”,否则输出“随机生成的点在矩形外部”。
