数模 | CPLEX求解指派/背包/选址问题，代码编写就是这么丝滑

前沿

​上一期阐述了用 Matlab调用linprog等函数 求解线性/整数规划 的编程思想和代码。

优点 是转化为矩阵，求解较快； 缺点 是不能很好地处理 含有多维变量或参数 的模型。(例如intlinprog函数只能处理一维数据)

而数模比赛时，构建的模型通常较为 复杂 (参数/变量繁多且均是多维)。因此，像线性/整数规划这种 专业的问题 ，有必要交给 专业的软件 。

不只是 CPLEX ，还有 Gurobi/AMPL 等，它们努力做到 让你专注于写模型 ，而无需在 模型转代码 上花费太多时间。毕竟它们是 商业软件 ， 简单好用才是王道 。总的来说，它们主要解决优化问题编程时的如下 痛点 ：

模型怎么写的，对照着编程就好了！(别费劲地要求我们去整理成比如矩阵等形式)；
很多模型长得差不多，主要是数据在变。(那编程时能否也分开，模型是模型，数据是数据，从而实现改数据时不用改模型)；
能否用简单的标记就能区分小数、整数、正负变量或参数。(标记好后让软件自己去区分，无需人为)

（以上三点结合上一期 Matlab调用linprog等函数 内容，会有更深体会）

听上去是不是感觉挺 美好 的？恩，但除了美好，我们还希望 简单 ！那如何才能实现呢？不着急，一起看个 例子 ，懂了它，就能掌握这类优化软件的 编程思想 啦。

一、CPLEX编程思想

仍以 之前 提到的 指派问题 为例：

指派问题：
分配n人去做n项工作；每人做且只做一项工作；若分配第i人去做第j项工作，需花费Cij成本。
问应如何分配工作使总成本最小？

建立的数学模型为：

仔细观察上述模型，有如下 特点 ：

参数有n、cij，均为整型；集合有[1..n]；变量有xij，为0-1布尔型；
定义模型时的符号有：最小化问题(minmize)、约束(subject to)；
定义约束时的符号有："求和号"、"任意号"；

找到了这些 关键元素 ，接下来就是 采用一定的逻辑 把它们串接起来~

我们知道， 参数和集合都是已知量 ；而 决策变量xij是未知量 。那肯定是先做好准备工作： 写好已知量，后再去写模型 。因此，CPLEX的编程步骤为：

1. 定义参数、集合、变量

首先盯着上面指派问题中的 目标函数 看，里面有 参数cij和n ；有 集合i,j∈1..n ；有 决策变量xij 。

不同软件编程语法的差异在于如何定义这些量。 如CPLEX用 dvar定义变量 ，而AMPL用var定义(下一期讲)。本期专注于CPLEX的语法。

(1) 定义参数——int/float
语法是： "int n=5”或者“int n=..."； 如果数据类型是连续型，int改为float，即可以是小数。

这里允许n先不定义它是多少，用 三个点 表示。这种写法实现的是 模型文件和数据文件分开写。

这样，模型文件中不用写数据，专注于写模型即可，而所有数据放在另一个文件中写。

当然， 模型文件中同时也包含所有数据 ，不再去编写数据文件，CPLEX也是支持的。

(2) 定义集合——range
语法是："range Worker = 1..n"

这里 Worker 是我随意起的名字； 1..n 中的 两个点 也是CPLEX语法，指 从1到n ，不可用1个点或3个点。

定义好了集合，模型中再遇到 i∈1..n 时，就可以简写成 i in Worker 了；也许有人会说，那直观写成 i in 1..n 也很简单呐，没必要再去定义个Worker吧。

道理确实是这样的，也确实 有时不去定义它 ，语法都是允许的，看大家的编程喜好了。

(3) 定义变量——dvar
语法是："dvar 数据类型 变量"；如"dvar boolean x[Worker][Job]"

dvar 的含义是 decision variable (决策变量)； boolean 是 布尔型 ，0-1变量的意思，含义是 当第i个Worker去做第j项Job时为1，否则为0 。

注意， x[Worker][Job] 也可写成 x[1..n][1..n] ，但 不能写成x[i][j] 。因为定义变量时，没有下标什么事，只有写模型时才会有下标的事。

此外， 数据类型 除了 boolean ，还有整型( int )，正整数( int+ )、连续型( float )等。如定义一个 正整数x 则为: "dvar int+ x" 。

2. 写模型——定义目标和约束条件

语法是："minimize 目标函数"、"subject to{约束;}"

CPLEX等软件编程能实现 "模型怎么写，程序怎么编" ，非常直观。下一节我会逐行展示。

这里多说几句。我们建模时，通常习惯使用" 集合语言" 。比如 求和号Σ ，在CPLEX中用 "sum" 表示；对 "任意的i∈1..n" ，用 "forall(i in 1..n)" 表示。

以上就是CPLEX(其他软件也适用)的 编程思想 ：

先定义已知量，再定义未知量，然后采用"集合语言"写目标和约束。

我编了个简单的口诀帮大家记忆： 参集变，mst。

参集变：
先写已知量"参数"和"集合", 再写未知量"决策变量"
mst：
"m"指最大/小化问题，即maximize、minimize; "st"为subject to{}的简写。

下面，针对 指派/背包/选址问题 ，按照" 参集变，mst "的编程步骤，实践下吧。

二、CPLEX求解指派问题

本节采用 模型文件和数据文件分开写 的模式，下一节 背包问题展现放在一起写 的模式。(对于任意模型，两种模式皆可的)

1. 定义参数、集合、变量

已知量 ： 参数 有n和cij； 集合 为1..n。都先不赋值，在数据文件中再给它们赋值。

int n=...; // 参数n
range Worker=1..n; // 工人集合
range Job=1..n; // 任务集合
int c[Worker][Job]=...; // 成本参数

未知量 ： 决策变量 为xij。

dvar boolean x[Worker][Job];  // 决策变量

上述" c[Worker][Job] "即 第i个Worker去做第j项Job 。如果大家还不习惯这种 借用字符串 的写法，也可以像下面这样写：

int n=...; // 参数n
int c[1..n][1..n]=...; // 成本参数
dvar boolean x[1..n][1..n];//决策变量

相比较， 少了定义集合的两行代码 。不定义集合的话，就需一直写着" 1..n "。

不管哪种，都比较简洁直观，即使没学过这些语法，也能懂个大概。两种方式看个人偏好啦。

2. 写模型——定义目标和约束条件

准备工作做好了，那就对照着模型， 逐行 翻译成CPLEX语言吧。

目标函数语法： minimize/maximize 目标函数

回顾 指派问题的目标函数 ，有两种编码方式：

minimize sum(i in Worker)sum(j in Job) c[i][j]*x[i][j];
minimize sum(i in 1..n)sum(j in 1..n) c[i][j]*x[i][j];

两种皆可，如果定义好了 集合 ，就用集合写；如果不习惯，用" 1..n "写也非常直观。

这里需要注意"()"和"[]"的使用规范 。" sum() "相当于函数，要用" () "；参数/变量 下标调用的时候是用"[]" ；写完结尾要用 ";" 。

约束条件语法： subject to{约束;}

回顾指派问题的约束条件：

subject to
{ forall(i in 1..n)
    sum(j in 1..n) x[i][j] == 1;//约束1
  forall(j in 1..n) 
    sum(i in 1..n) x[i][j] == 1;//约束2
}

以约束1为例，第2行" forall(i in 1..n) "对应图片中右半部分；第3行 对j求和后等于1 就是约束1。不需要转化成矩阵啥的，语法很人性化。

依然需要注意"()"和"[]"的使用规范 。" forall() "相当于函数，要用" () "，结尾记得加 ";" 。好了，模型就这么愉快地 翻译 完啦，再新建个 数据文件存储数据 吧。

新建数据文件： Assignment.dat

之前模型编码存放于" Assignment.mod "文件中，新建后缀为 .dat 的文件存储数据：

n=3; // 3个工人去完成3个任务
c=[[3,8,2],[8,4,6],[6,2,10]]; // 成本矩阵

两行代码搞定， 注意这里的矩阵写法 。该写法类似Python，数据结构为数组； 两个数字之间的","不可省略 奥。

3. 运行CPLEX并求解

CPLEX的安装教程放在文末。安装成功后，打开CPLEX，关闭欢迎界面，选择" 文件 "--" 新建 "-- "OPL项目 "。

起个名字，如" Assignment "，并 勾选上 图中的三个选项。

这里要注意： 项目名称和位置必须是英文， 不能出现中文，否则无法运行 。

在新建的 "Assignment.mod"文件 中输入模型代码，在 "Assignment.dat" 文件中输入数据代码。

注意，在运行程序前， 还有个地方要改 ：

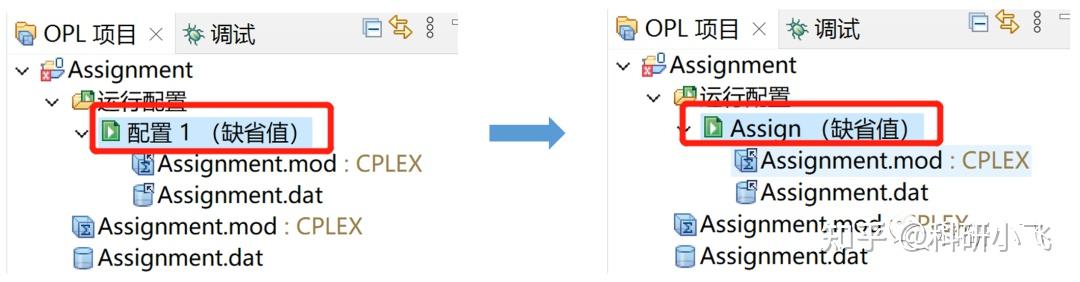
新建完两个文件后，项目栏默认会写" 配置1(缺省值) "。虽然是默认的，但出现中文是不行的，所以要 改成英文 ，随便起个 英文名 即可。

然后，在改完名后的" Assign(缺省值) "上右键，点击" 运行这个 "，没有报错的话，就能在下方看到" 解决方案 "。

可见，目标值是11，最优解x的值也已给出。点开" 统计信息 "还有 计算时间 等数值。

以上就是 CPLEX求解指派问题 的步骤。记住" 参集变，mst "这句口诀，写代码就像吃德芙一般丝滑。

三、CPLEX求解背包问题

本节展示 模型和数据写在一起 的形式，即仅写一个 ".mod"文件 即可。

背包问题：
往一个承重为W的背包中，装入重量和价值都不同的物品。 每个物品的重量为wi，价值为vi。
问：应装哪几件物品，使得装入背包的物品总价值最高？

建立的数学模型为：

(其中，xi为决策变量，选第i个物品时为1，不选时为0)

同样按照" 参集变，mst "的步骤来编程吧。

参集变：
参数 是n、W、wi和vi； 集合 是1..n； 变量 是xi；

int n=4; // 假设是4个物品
int W=15; // 假设最大承重为15