基于机器学习的电池寿命预测 MATLAB 代码

引用的是MIT这篇论文：

[1] Severson, K.A., Attia, P.M., Jin, N. et al. "Data-driven prediction of battery cycle life before capacity degradation." Nat Energy 4, 383–391 (2019). https:// doi.org/10.1038/s41560- 019-0356-8

原文在线查阅地址： Data-driven prediction of battery cycle life before capacity degradation (mit.edu)

实验数据以及说明： Experimental Data Platform (matr.io)

[2] Experimental Data Platform

对于我种外行来说，看文字真不如看代码来得方便，等有空了再去看看论文原文。

于是，我打算先来看看 MathWorks 提供的一个 类似的案例代码快速入个门，入门，入门 。

代码均来自于官方案例：「 Predictive Maintenance Toolbox ，本例使用线性回归模型【Linear regression】来预测快充使用场景下的锂电池剩余循环寿命，这是一种有监督机器学习方法。
这个案例也是参考的这篇论文，数据也是来自这篇论文，所以权学习这篇论文的pre-work。

• 本例使用线性回归模型【Linear regression】来预测快充使用场景下的锂电池剩余循环寿命，这是一种有监督机器学习方法。
• 基于物理机理来实现锂电池寿命预测非常复杂，因为本身电池工况差别，而且就算是同一个电池厂家的电池本体也有差别。
• 如果有足够的测试数据，或许机器学习方法能给我们提供一个“还行”的结果。
• 这个例子里，取电芯前100个充(放)电循环数据，设计特征量，用来预测剩余寿命(这里的预测误差在 10%)。

数据集

根据原论文作者的数据说明，实验是为了做快充优化的，所以基本上所有的实验设计重点是各种不同的充电过程。

下载

MATLAB命令行运行如下代码，下载数据：

url = 'https://ssd.mathworks.com/supportfiles/predmaint/batterycyclelifeprediction/v1/batteryDischargeData.zip';
websave('batteryDischargeData.zip',url);
unzip('batteryDischargeData.zip')
load('batteryDischargeData');

下载解压缩后有2.3GB的 batteryDischargeData.mat 文件：

文件里有三个一样的结构体，一共是 124个电芯循环实验，分为 test, train, val 三组。

原论文提供的三批次实验数据：

• 电芯：lithium-ion phosphate磷酸铁锂(LFP)/石墨，A123 Systems (APR18650M1A)
• 标称容量：1.1Ah
• 标称电压：3.3V
• 环境温度 ：控制在30degC（电芯温度是变化的）

数据说明

比如 testData 这个结构体，1*40,表示有40个电芯数据，每 一行对应一个电芯从新到老的循环 数据。

• barcode和channel_id：电池编号记录
• cycle_life: 电芯循环寿命
• cycles: 循环过程详细数据
• summary: 简化的描述改电芯生命周期的数据
• Vdlin: 电压采样测量点，从3.5V到2.0V，取1000个点，0.15mV一个点；

policy和policy_readable：充电策略描述（这部分参见原数据说明，三批实验数据有差别，大体如此，不影响后续的部分）。

• 命名方式： “C1(Q1)-C2 ”= ”第一段充电倍率，放电切换点SOC%，第二段充电倍率”
• 第二段冲到 80% SOC后，改为 1C 充电；
• 电压到顶后，改为 CC-CV（Constant-current constant-voltage battery charger）充电，C/50；
• 所有放电倍率均为4C

比如下图是第一行的某 一个 循环充电过程：

• 先以5C(近似)充电 =》在SOC上升67%的时候，切换4C(近似)充电 =》充到80%的时候，静置一会儿(不同的测试静置时间不同) =》然后1C充电=》C/50的恒压恒流充电
• 4C放电放到完

% 这部分需要下载论文原数据，不过只是为画下面这张图，不重要，跳过。
i = 1; %第一个电芯
subplot(3,1,1)
plot(batch(i).cycles(1).t,batch(i).cycles(1).I)
xlabel('time');ylabel('Current');
subplot(3,1,2)
plot(batch(i).cycles(1).t,batch(i).cycles(1).V)
xlabel('time');ylabel('Voltage');
subplot(3,1,3)
plot(batch(i).cycles(1).t,(batch(i).cycles(1).Qc - batch(i).cycles(1).Qd)/1.1);% 很神奇的是放电量和充电量是分开记录的
xlabel('time');ylabel('SOC');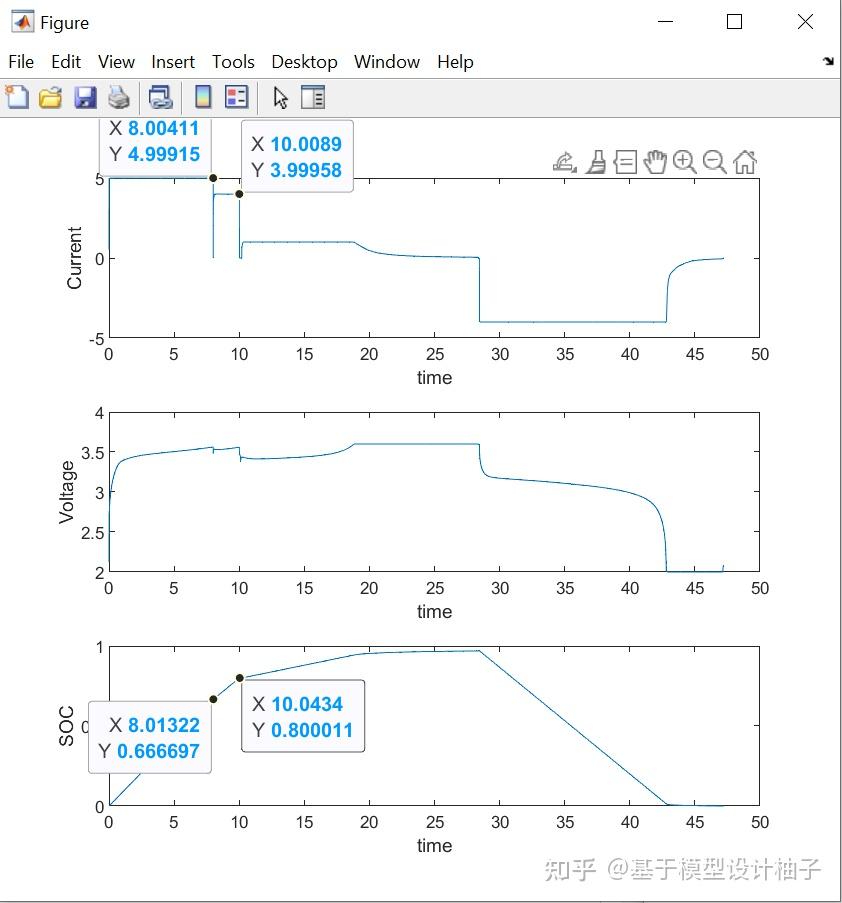

Cycle Summary:

循环周期-放电容量-内阻-充电时间

比如第6个电芯的容量和内阻随着循环次数的衰退：

i = 6;% 电芯编号
subplot(2,1,1)
plot(trainData(i).summary.cycle,trainData(i).summary.QDischarge); % 注意如果是画原始数据，有些 i = 1的曲线是空值
xlabel('cycle');ylabel('QDischarge');ylim([0.5,1.25]);
subplot(2,1,2)
plot(trainData(i).summary.cycle,trainData(i).summary.IR);
xlabel('cycle');ylabel('IR');ylim([0.01,0.025]);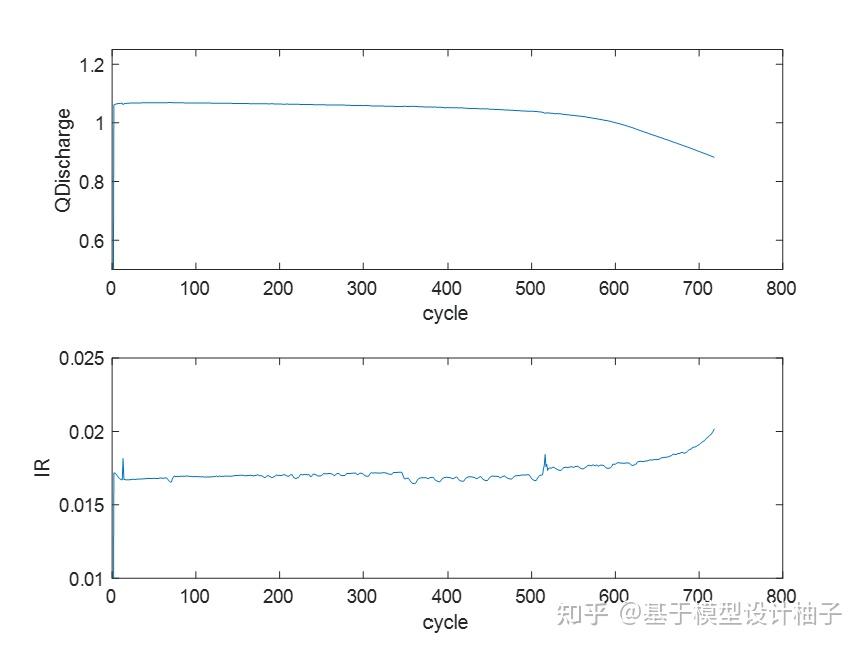

MATLAB 的例子取了其中的一部分数据，原始的内容会多一些。

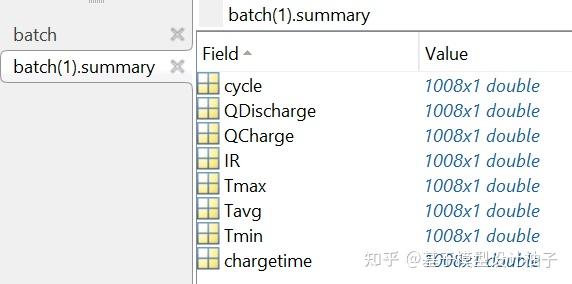
cycles:

时间-温度-电压采样点对应的电量（对应刚才的Vdlin）

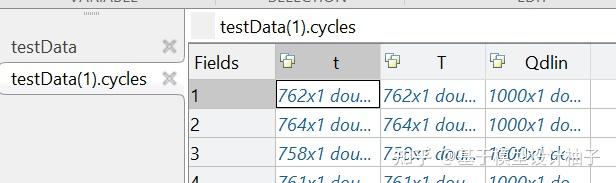
原始数据会多一些信息，刚才的充电过程就是用这里的数据画的。因为这个MATLAB的例子没用上，于是就删掉了。

特征量提取

特征量

放电容量似乎可以视为电池健康状态的一个关键特征，刚刚的图上能看到它是随着循环次数逐渐衰减的。

下面这个代码把各个电芯前1000个循环的放电容量画出来，观察放电容量在生命周期中是如何衰减的。

figure, hold on;
for i = 1:size(trainData,2)
    if numel(trainData(i).summary.cycle) == numel(unique(trainData(i).summary.cycle))
        plot(trainData(i).summary.cycle, trainData(i).summary.QDischarge);      
ylim([0.8,1.1]);
ylabel('放电量 [Ah]');
xlabel('循环数');
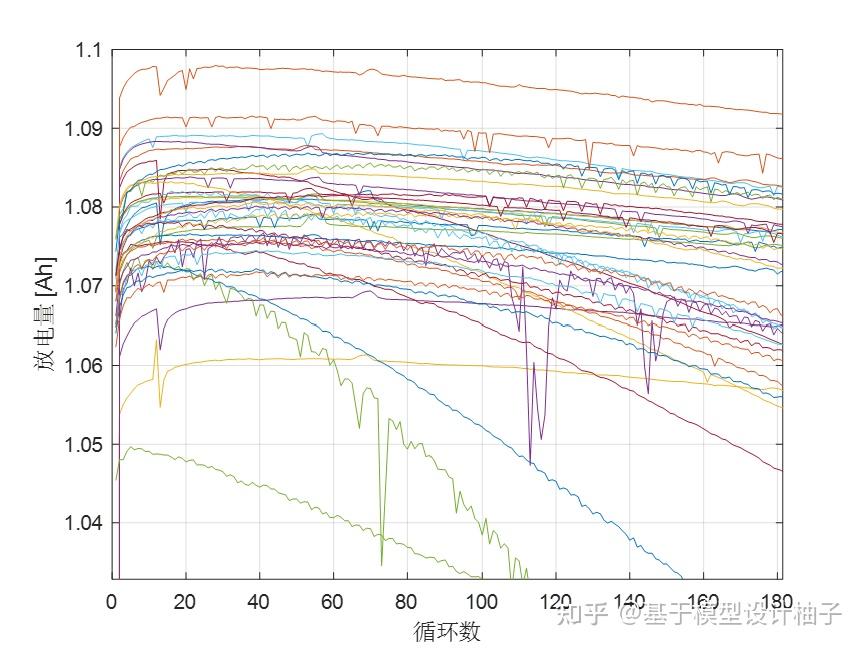
%这里显示的放电容量的spikes是实验问题引起的，不用管它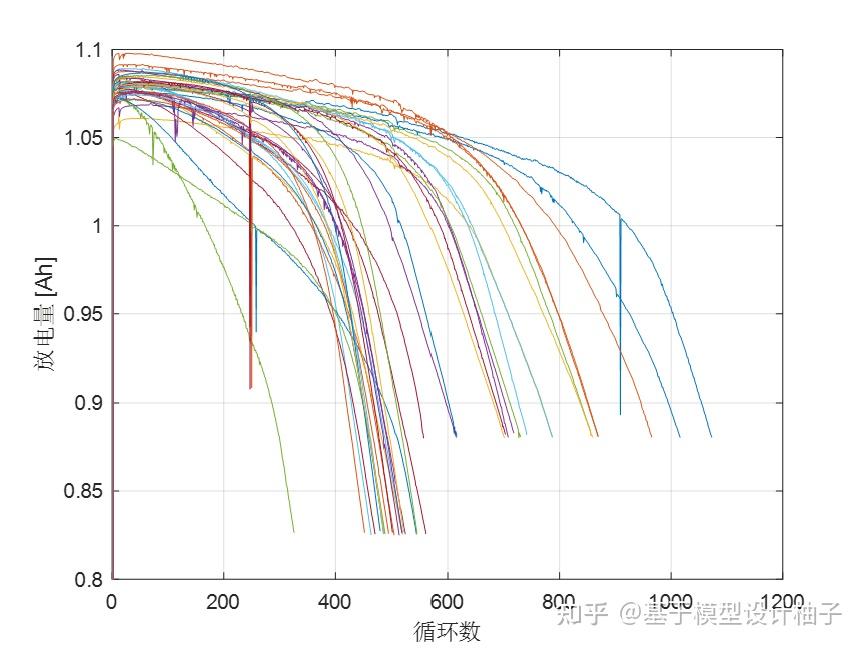

从图上可以看出，在电池寿命快结束时，容量衰减会突然加速衰减。然而，如果我们要用短周期来做预测的话，在前100个周期中（见下方放大的图片），电芯容量衰减很少，不是很明显。这样放电容量就不太能 直接 作为电池寿命预测的特征量。

% 第41个电芯的 QvsV 曲线衰减过程
cc = parula(numel(trainData(41).summary.cycle));
figure; clf;
for k = 1:numel(trainData(41).summary.cycle)
    plot(trainData(41).cycles(k).Qdlin, trainData(41).Vdlin, 'Color', cc(k,:));
    hold on;
hold off;
clrb = colorbar; %* colorbar
set(clrb, 'TickLabels', {'1','257','514'}, 'Ticks', [0,0.5,1]);
clrb.Label.String = '循环数';
xlabel('放电量 [Ah]');
ylabel('电压 [V]');
title('放电量：电芯41');

这是第41个电芯的所有循环的QV曲线合集。看图例，从蓝到黄色循环次数越大。也就是说，电芯越老，这条曲线越往左飘。

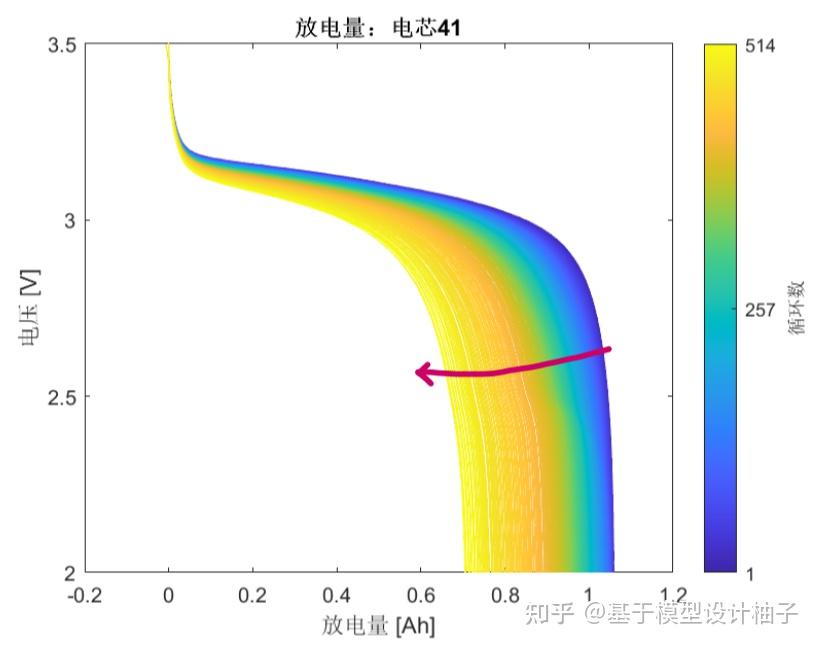
%===以下可以跳过

那么怎么描述这种 飘 呢？比如，我们画其中的三条曲线，第[10,100,500]条：

% 第41个电芯的 QvsV 曲线衰减过程
cc = parula(numel(trainData(41).summary.cycle));
figure; clf;
for k = [10,100,500]
    plot(trainData(41).cycles(k).Qdlin, trainData(41).Vdlin, 'Color', cc(k,:));
    hold on;
hold off;
clrb = colorbar; %* colorbar
set(clrb, 'TickLabels', {'1','257','514'}, 'Ticks', [0,0.5,1]);
clrb.Label.String = '循环数';
xlabel('放电量 [Ah]');
ylabel('电压 [V]');
title('放电量：电芯41');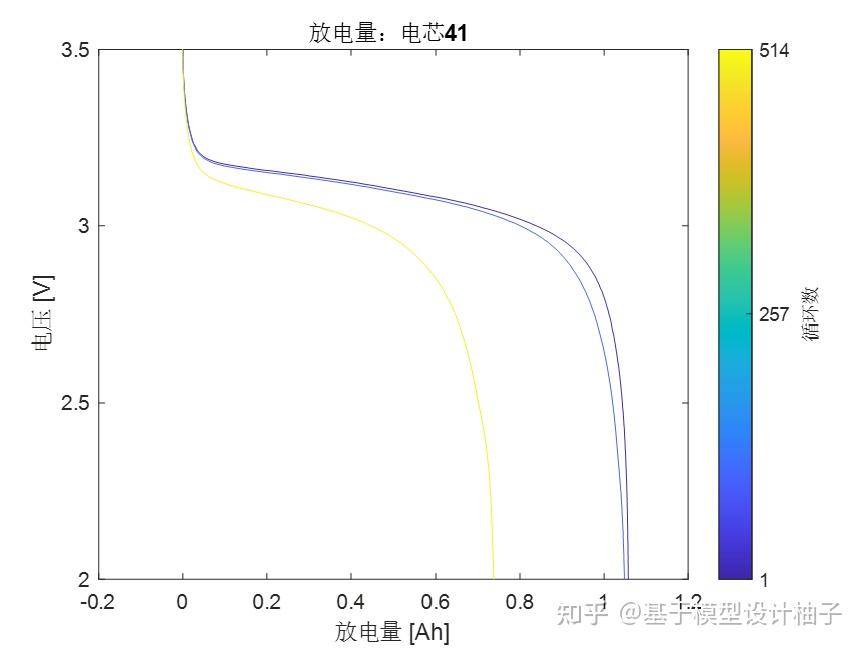

如果我们直接用曲线相减，那得到的是一个向量。比如用第100个循环减去第10个循环的值：

trainData(i).cycles(100).Qdlin - trainData(i).cycles(10).Qdlin

所以就用了两条曲线的差值的方差：

var(trainData(i).cycles(100).Qdlin - trainData(i).cycles(10).Qdlin)

我顺便画了下单个电芯的方差随着衰减的变化过程

% 第41个电芯的 QvsV 曲线衰减过程
figure; clf;
for k = 1:numel(trainData(41).summary.cycle)
    kVar(k) = var(trainData(i).cycles(k).Qdlin - trainData(i).cycles(10).Qdlin); %取方差
plot(1:k,kVar);
xlabel('循环数 ');
ylabel('方差');
title('放电量：电芯41');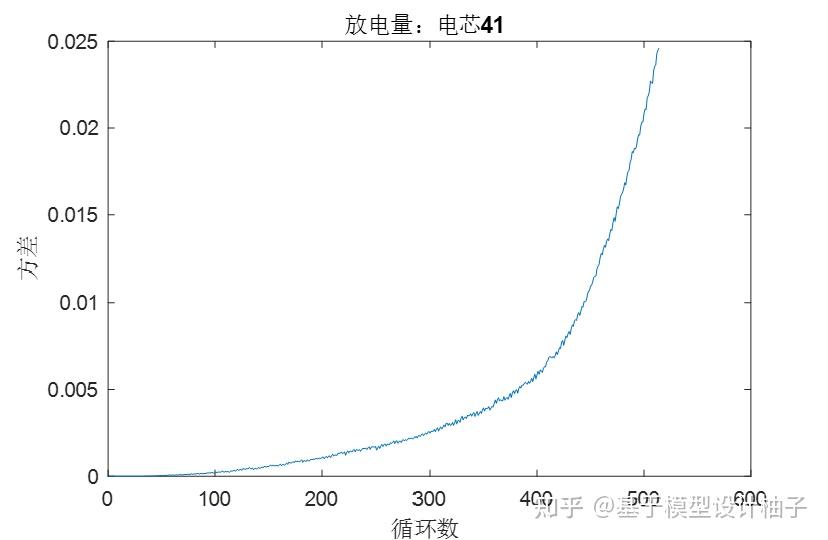

像个很好拟合的二次曲线。

于是很好奇，画一下全部电芯的曲线。

下图方差增加的越多，显然是老的越快的。如果能建立一个这个二次曲线形态变化和工况的关系，似乎就能准确的预测出寿命。

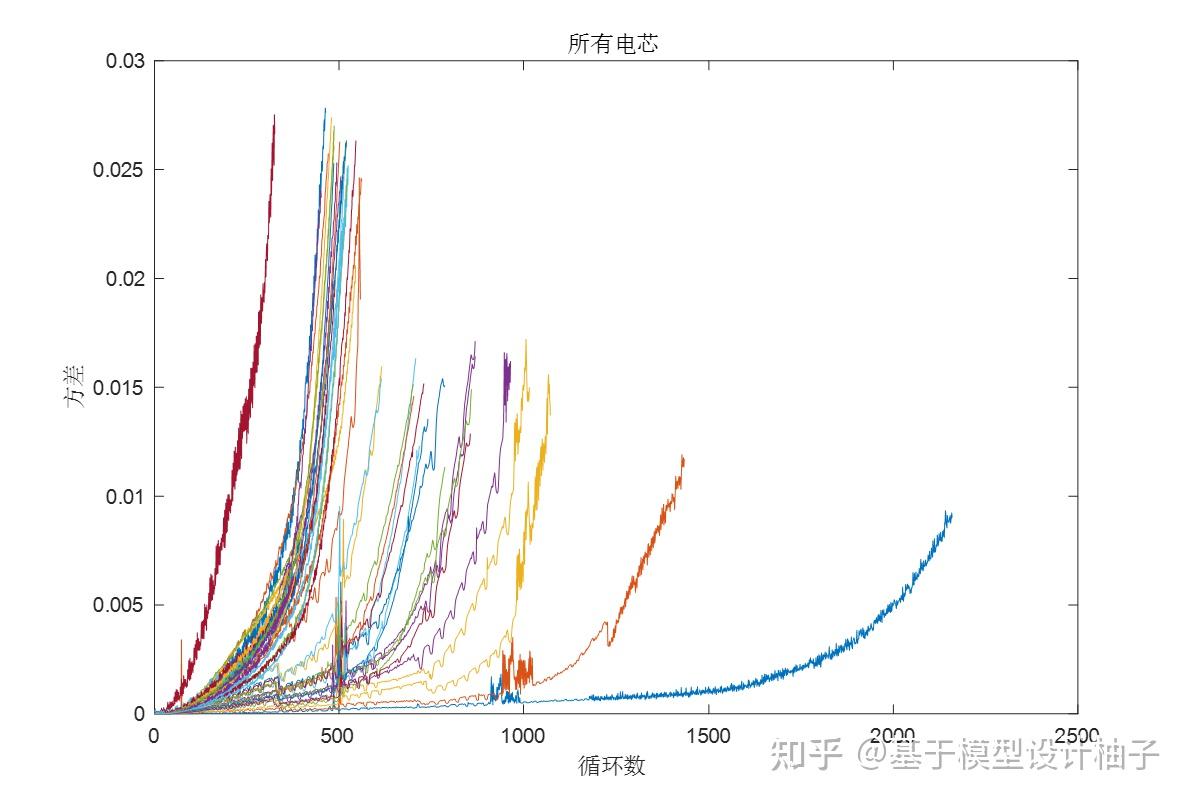
%===以上可以跳过，以下继续

原代码的描述方式也很有意思，它建立了每一个电芯 Q100-10的方差 和 总寿命 的关系：

figure;
trainDataSize = size(trainData,2);
cycleLife = zeros(trainDataSize,1);
DeltaQ_var = zeros(trainDataSize,1);
for i = 1:trainDataSize
    cycleLife(i) = size(trainData(i).cycles,2) + 1; % 第i个电芯的总循环次数
    DeltaQ_var(i) = var(trainData(i).cycles(100).Qdlin - trainData(i).cycles(10).Qdlin); %第i个电芯的的 Q100-10 方差
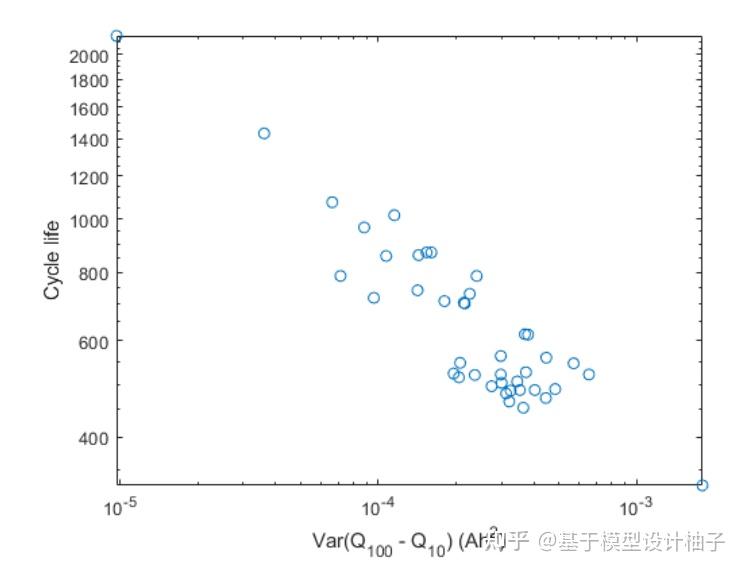
loglog(DeltaQ_var,cycleLife, 'o')
ylabel('Cycle life'); xlabel('Var(Q_{100} - Q_{10}) (Ah^2)');

这是得到的图，

• 横坐标是电芯循环到100次时，电容量曲线衰减方差(和第10次循环对比)；
• 纵坐标是它未来的总寿命；
• 横纵坐标都取了 log ；

8 种特征量

案例里提供了8种特征量， 只取前面100个循环的数据 ，用于预测。

[XTrain,yTrain] = helperGetFeatures(trainData);
head(XTrain)

特征量计算函数案例里提供了。y就是对应的循环寿命/次数。

DeltaQ_var

• 就是上图的横坐标，最里面是：每个电芯第100次循环的放电容量曲线 - 第10次循环的放电容量曲线的差值
• log10(abs (var(batch(i).cycles(100).Qdlin - batch(i).cycles(10).Qdlin) ));
• var 求方差
• abs 求绝对值

DeltaQ_min

• log10(abs(min(batch(i).cycles(100).Qdlin - batch(i).cycles(10).Qdlin;)))；
• 和上面类似，只是不取方差了，只取了曲线差值的最小值。

拟合从第2个到第100个循环的容量衰减曲线 QDischarge vs cycle，线性拟合，比如第4个电芯的曲线：

i = 4;
figure
plot(trainData(i).summary.cycle(2:100), trainData(i).summary.QDischarge(2:100));   
coeff2 = polyfit(trainData(i).summary.cycle(2:100), trainData(i).summary.QDischarge(2:100),1);
y1 = polyval(coeff2,trainData(i).summary.cycle(2:100));
hold on
plot(trainData(i).summary.cycle(2:100),y1,'o')
hold off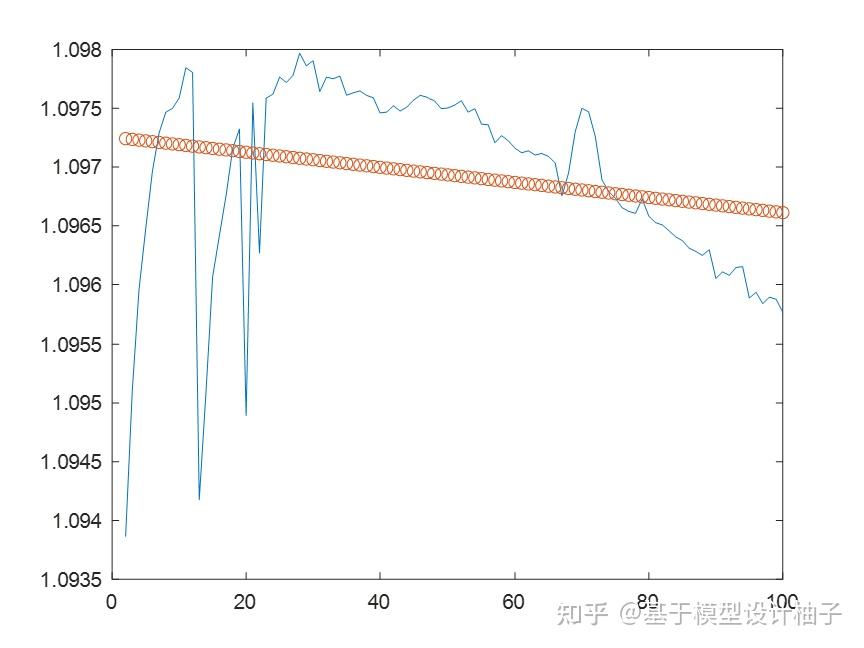

CapFadeCycle2Slope

• 拟合结果的斜率 CapFadeCycle2Slope(i)=coeff2(1);

CapFadeCycle2Intercept

• 拟合结果的截距 CapFadeCycle2Intercept(i)=coeff2(2);

Qd2

• 第2个循环的电芯电量：batch(i).summary.QDischarge(2)

AvgChargeTime

• 从第2到第6个循环的平均充电时间 ：mean(batch(i).summary.chargetime(2:6))

MinIR

• 从第2到第100个循环的最小内阻 ：MinIR(i) = min(temp(batch(i).summary.IR(2:100)~=0));

IRDiff2And100

• 从第2到第100个循环的内阻差值：batch(i).summary.IR(100) - batch(i).summary.IR(2)

以上是所选择的特征向量的解释。

机器学习

准备好了数据就可以开始来训练模型了。

随便试一下先

先随便来（和MATLAB原代码不一样）。

机器学习 App

打开 Regression Learner，点击 New Session:

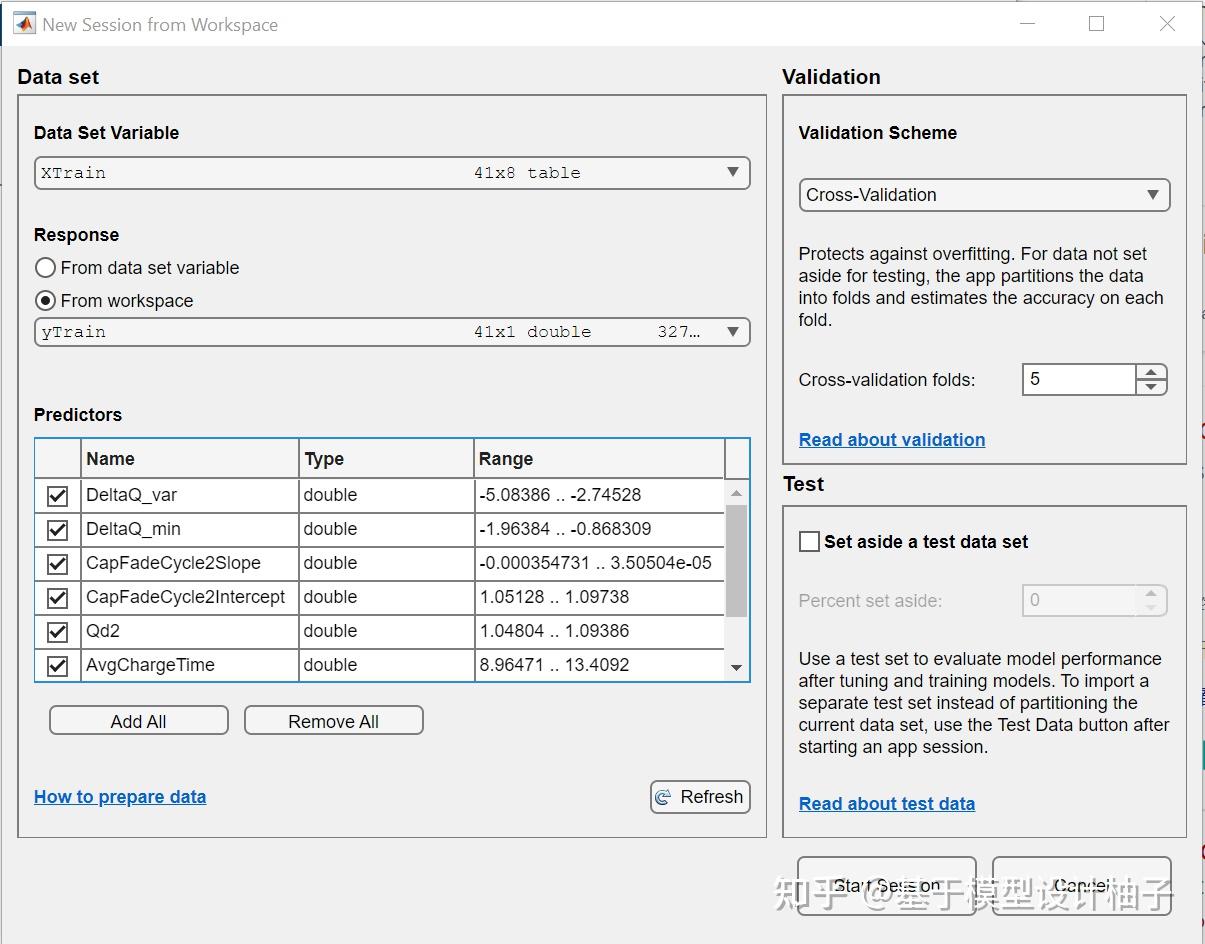
在弹出的窗口中选择：

• Data Set Variable: XTrain
• Response: From workspace yTrain
• Start Session

选择：

1. All Quick-To-Train 或者 All 都可以，随便
2. Train All

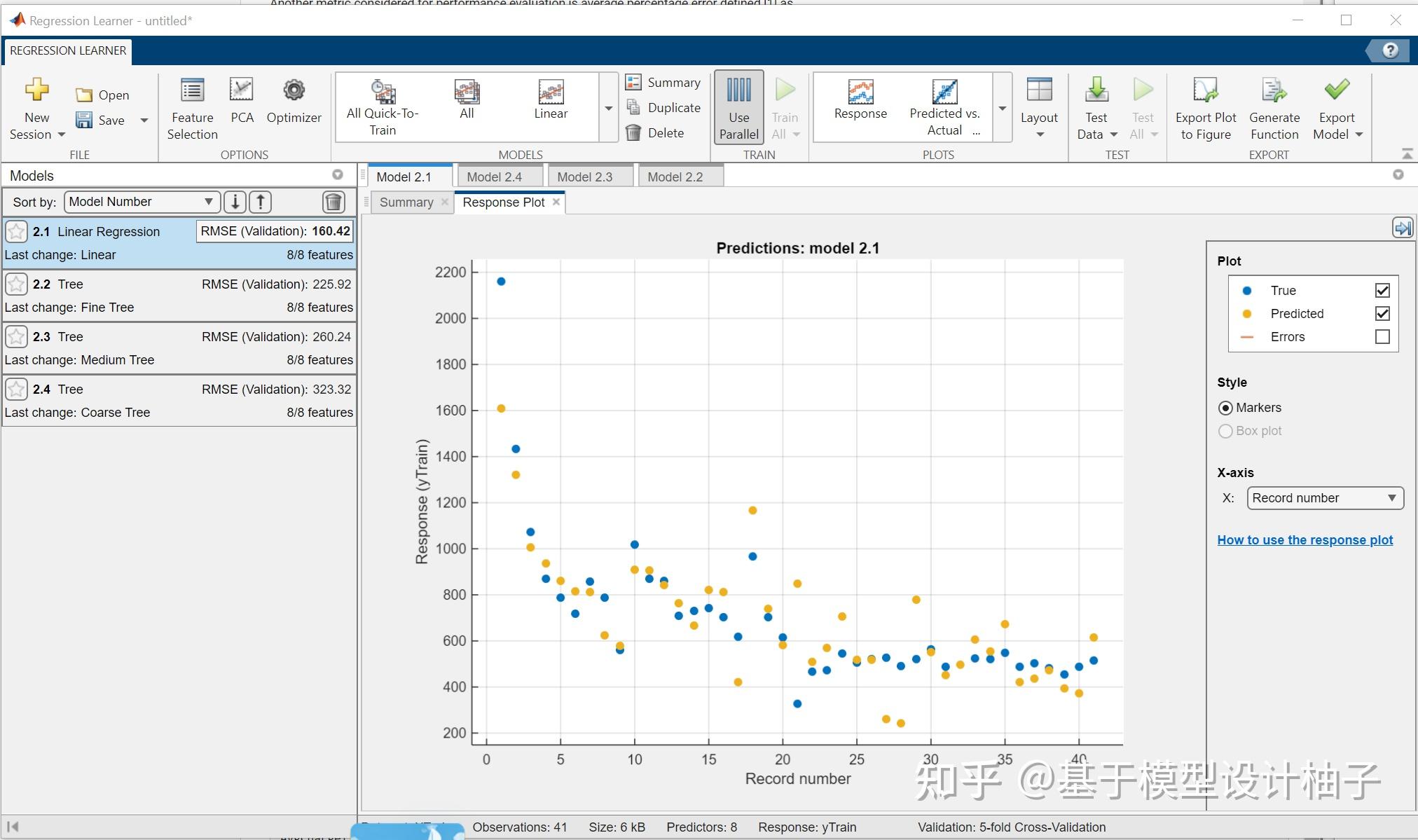
学习了一些基本模型，对比之下线性回归模型的RMS误差最小。如果需要，可以选择其它模型进行学习。

学习完之后，可以导出模型【Export Model】，把结果保存到 workspace。

默认变量名：「trainedModel」。

结果评估

[XTest,yTest] = helperGetFeatures(testData);
yPredTest = trainedModel.predictFcn(XTest);

画图

figure;
scatter(yTest, yPredTest);
hold on;
refline(1, 0);
title('预测剩余寿命 vs 实际剩余寿命')
ylabel('预测剩余寿命');