（一）线性方程组求解

包含n个未知数，由n个方程构成的线性方程组为：

其矩阵表示形式为：

其中

一、直接求解法

1、左除法

x=A\b;

如果A是奇异的，或者接近奇异的。MATLAB会发出警告信息的。

2、利用矩阵的分解来求解线性方程组（比单单进行左除速度快）

（1）LU分解(只有方阵可以使用)

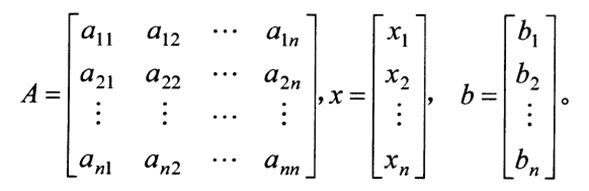
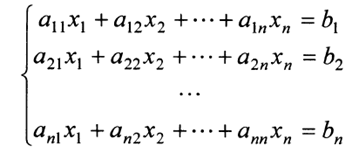LU分解就是分解成一个交换下三角矩阵（也就是说进行一定的操作后才是下三角矩阵）和一个上三角矩阵（不需要变换）的乘积形式。只要A是非奇异的，就可以进行LU分解。

MATLAB提供的LU分解函数对于矩阵进行LU分解：

[L,U]=lu(X);      %X必须是方阵
[L,U,P]=lu(X);    %PX=LU。X必须是方阵

实现LU分解之后，线性方程组Ax=b的解就为x=U\(L\b)或x=U\(L\Pb)、

（2）QR分解（A是非奇异的）

QR分解就是分解成一个正交矩阵Q和一个上三角矩阵R的乘积形式。只要A是非奇异的，就可以进行QR分解。QR只能对方阵进行分解。

[Q,R]=qr(X);        %X=QR
[Q,R,E]=qr(X);      %XE=QR

实现QR分解之后，解为x=R\(Q\b)或x=E(R\(Q\b))。

（3）Cholesky分解（X是正定的）

如果X是正定的。则将矩阵分解成一个下三角矩阵和上三角矩阵的乘积。上三角矩阵为R，下三角矩阵为其转置，X=R’R.

MATLAB进行CHolesky分解方法：

R=chol(X);
[R,p]=chol(X);        %p=0则为正定矩阵，返回一个R，或者p为一个正整数q=p-1，满足R'R=X(1:q,1:q)

则线性方程组的解为x=R\(R’\b)

二、迭代法求解(求解大型系数矩阵的方程组）

1、Jacobi迭代法

（1）原理解释

对于Ax=b，如果A为非奇异，那么A就可以分解成一个对角阵D，一个下三角阵L和一个上三角阵U，使得A=D-L-U。则

然后得到迭代公式为

如果收敛的话，就可得到方程的解。

（2）MATLAB编程求解（= =，很简单的迭代。但是如果没有解的话，会得到NAN= = ）

function [y,n]=jacobi(A,b,x0,eps)
%A为系数矩阵，b为向量，x0为初值。
if nargin==3      %输入参数至少为3个
    eps=1.0e-6;
elseif nargin<3
    error
    return
D=diag(diag(A));   %求A得对角矩阵
L=-tril(A,-1);     %求A的下三角阵（没有对主对角线），由于是拆成A=D-L-U，所以前面加了“-”号，下同   
U=-triu(A,1);      %求A的上三角阵（没有对主对角线）。
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;        %迭代次数
while norm(y-x0)>=eps
    x0=y;
    y=B*x0+f;
    n=n+1;
（3）一个demo
    0.9958
    0.9579
    0.7916
2、Gauss-Serdel迭代法
（1）原理说明
        由于每一次的x都已经算出来了，就没比较再从头算一次了。就是省略了无效的迭代次数，然后我们就得到一个新的迭代公式。
（2）MATLAB编程求解
function [y,n]=gauseidel(A,b,x0,eps)
%A为系数矩阵,b为列向量,x0为初值。
if nargin==3
    eps=1.0e-6;
elseif nargin<3
    error
    return
D=diag(diag(A)); %求A的对角矩阵
L=-tril(A,-1);   %求A的下三角阵
U=-triu(A,1);    %求A的上三角阵
G=(D-L)\U;
f=(D-L)\b;
y=G*x0+f;
n=1;
while norm(y-x0)>=eps
    x0=y;
    y=G*x0+f;
    n=n+1;
     使用迭代法，一般只能找到一组解（离初值最近的解）。然后使用迭代法，一定要能收敛才能够使用。
（三）——常微分方程初值问题的数值解法
      一般是比较难解出来解析解，所以一般求得离散解就很不错了。
一、龙格——库塔法简介
1、由中值定理可得：
     所以，根据上述递推式之后能够计算未知函数y在点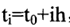，i=0,1，……，n的一列的数值解。
     当然，使用的递推公式都会有一个误差累计的问题，所以我们使用龙格——库塔公式：
2、MATLAB封装的龙格——库塔法实现
[t,y]=ode23('fname',tspan,y0);
[t,y]=ode45('fname',tspan,y0);
其中，fname是定义f(t,y)的函数文件名，该函数文件必须返回一个列向量。
         tspan形式为[t0,tf]，表示求解区间。
         y0是初始状态列向量。
         t，y分别给出求解的相应向量。
然后自己会自动采用步长大小，所以效率还是不错的。
3、demo1
MATLAB编程求解
t0=0;tf=10;
y0=2;
[t,y]=ode23('funt',[t0,tf],y0);    %龙格——库塔法的离散解
y1=sqrt(t+1)+1;      %精确解
plot(t,y,'-b*');
hold on;
plot(t,y1,':ro');
红色是精确解，蓝色是离散解，可以得到差距不大。
4、demo2
     对于高阶的常微分方程。首先要转换为一阶常微分方程组。即状态方程（上面有两点表示二次导数= =）
令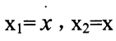：，则原式化为
MATLAB求解
t0=0;tf=20;
x0=[0;0.25];
[t,x]=ode23('funt',[t0,tf],x0)
subplot(1,2,1);plot(t,x);
subplot(1,2,2);plot(x(:,1),x(:,2));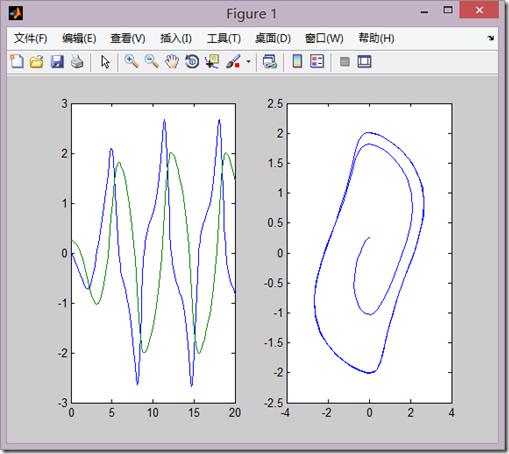
 
（四）函数极值
1、MATLAB求解方法
x=fmin('fname',x1,x2);       %求单变量函数的最小值
x=fmins('fname',x0);         %求多变量函数的最小值
 
2、没有求最大值的方法，但是我们可以通过求-fmin(-f(x))的方法求最大值