Scan Context 介绍及理解

扛着相机的翻译官

既然选择了远方，便只顾风雨兼程

Scan Context 由韩国KAIST大学的 Giseop Kim, Ayoung Kim 于2018年发表在 IROS (International Conference on Intelligent Robots and Systems)

论文：Kim, Giseop, and Ayoung Kim. "Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map." 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . IEEE, 2018.

开源工程： https:// github.com/irapkaist/sc ancontext

目前已经集成在了一些开源工程中

Scan Context 应用于基于3D点云的重定位和场景识别，主要思想是将场景3维信息压缩，将笛卡尔坐标系的信息转换到极坐标系下计算。

优势是高效利用场景点云分布特征，引入"旋转不变性"描述子，快速搜索。

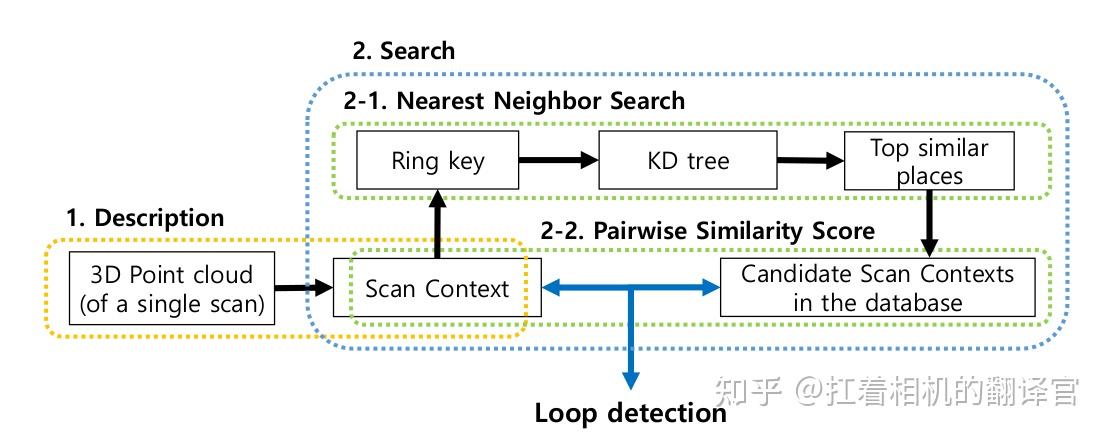
1.主要流程：

读取单帧3D点云数据，建立Scan-Context，在Mapping过程中生成KeyFrame中查找，使用Ring-key在KD-tree下查找最近邻结果，结果计算统计得分，得到最佳匹配，完成回环检测。

2.Scan-Context描述子

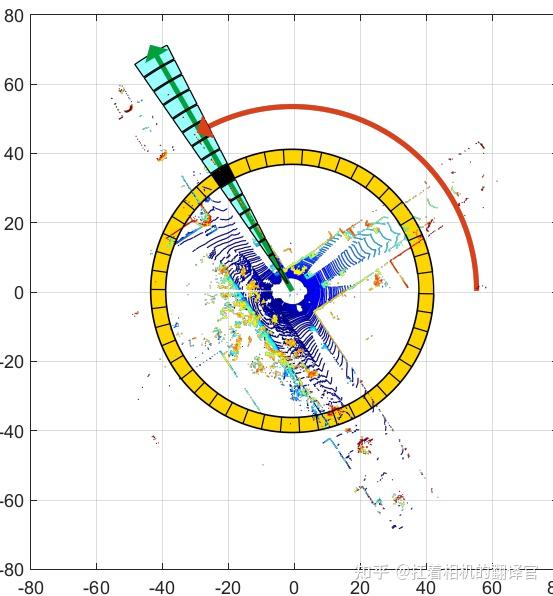
Scan-Context描述子如图所示，

Ring为黄色圆环，
Sector为青色部分，

SectorRing类似于极坐标中的角度，Sector类似于极坐标中的长度，3D物理空间被Ring和Sector划分成2D的“区块”空间，每个区块由Ring和Sector唯一确定。同时，将所需相关信息存放在每个区块中，比如：区块中的点云数量、区块中的点云max height、区块中的点云mean height等；

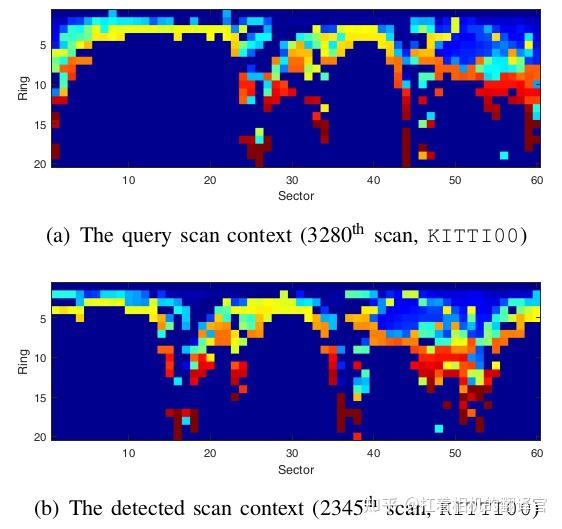
Scan-Context的表示为Ring-Sector矩阵，如图所示：Sector的数量为60，表示0~360°，每个Sector的分辨率为6°；Ring的数量为20，表示距离0~ L_{max} ；

图中(a)和(b)为同一场景下的两帧数据所形成的Scan-Context，可以看出，两个矩阵图像除去水平方向的位移偏差外，是高度相似的。这就是刚刚提到的“旋转不变性”；

也就是说，即便是每次采集数据的角度偏差很多，采集的点云数据也可以通过本描述子找到对应的场景。直观能想到的，只要每次将其中的一个矩阵图像水平移动一个单位，然后计算两个矩阵的相似度，最终一定能找到对应的结果；

抛开计算效率，先来看一下计算相似度的计算公式：

d(I^{q},I^{c}) = \frac{1}{N_s}\sum_{j=1}^{N_s}{(1-\frac{c^{q}_j \cdot c^{c}_j}{\parallel c^{q}_j \parallel \parallel c^{c}_j\parallel})} (1)

I^{q},I^{c} 分别是两个Scan-Context，相似度是每一列的对比之和，余弦距离(cosine distance)作为计算其中列向量 c^{q}_j , c^{c}_j 的方法 (注意：相似度越高与余弦距离越小)， N_s 是列数，也就是一个Scan-Conetext中Sector的数量；

将 I^{c} 沿列方向平移n个单位为 I^{c}_n , 那么可以遍历移动这个列向量 N_s 次，得到每次移动后相似度的结果，取最小值为 I^{q},I^{c} 的相似度:

D(I^{q},I^{c})= \min_{n\in[N_s]}d(I^{q}, I^c_{n}) (2)

n^*=\mathop{\arg\min}_{n\in [N_s]}{d(I^q,I^c_n) } (3)

从理论上，使用当前帧Scan-Context遍历历史所有Scan-Context一定能找到对应的结果，即相似度的全局极值。但从效率上，这并不可取，我们还需要更快的方式。于是引入了Ring-Key。

3.Ring-Key描述子

Ring-Key是一种旋转不变描述子，具体表示为一位数组 k ，数组中每个元素 \psi(r_i) 为第 i 个Ring的编码值， r_i 的排布为距离原点从近到远；

k=(\psi(r_1),...,\psi(r_{N_r})), where \ \psi : r_i\rightarrow \mathbb{R } (4)

\psi(r_i)=\frac{|| r_i ||_0}{N_s} (5)

(5)为 \psi 的表达式，其中 || r_i ||_0 表示 r_i 中的非零数量；

Ring-Key相当于对数据进行了压缩和降维，而由于Ring-Key是旋转不变描述子，所以两个Scan-Context做匹配的时候可以直接对比Ring-Key的相似度，而不用直接使用(2)的方式，至此有了高效的匹配方式。

4.加速匹配

论文中使用Ring-Key构建kd-tree来查找相似候选帧，再进行匹配计算；

在开源代码中，其实还使用到了与Ring-Key类似的Sector-Key的概念，同样起到了数据降维和搜索加速的作用。

5.代码

不同工程中的Scan-Context的具体细节不同，我们以 SC-LeGO-LOAM 嵌入的Scan-Context为例；

5.1.Scan-Context的生成函数：

MatrixXd SCManager::makeScancontext( pcl::PointCloud<SCPointType> & _scan_down )

5.1.1.其中Scan-Context的数据结构：

 // main
 const int NO_POINT = -1000;
 MatrixXd desc = NO_POINT * MatrixXd::Ones(PC_NUM_RING, PC_NUM_SECTOR);

5.1.2.使用雷达安装高度外参，将点云移动至z方向大于零的区域，同时将直角坐标系转换为极坐标系：

  pt.x = _scan_down.points[pt_idx].x; 
  pt.y = _scan_down.points[pt_idx].y;
  pt.z = _scan_down.points[pt_idx].z + LIDAR_HEIGHT; // naive adding is ok (all points should be > 0).
  // xyz to ring, sector
  azim_range = sqrt(pt.x * pt.x + pt.y * pt.y);
  azim_angle = xy2theta(pt.x, pt.y);

5.1.3.矩阵中的每个元素为z的最大值：

// taking maximum z 
if ( desc(ring_idx-1, sctor_idx-1) < pt.z ) // -1 means cpp starts from 0
     desc(ring_idx-1, sctor_idx-1) = pt.z; // update for taking maximum value at that bin

5.2.Ring-Key的生成函数，提取的是行向量的均值：

MatrixXd SCManager::makeRingkeyFromScancontext( Eigen::MatrixXd &_desc )
     * summary: rowwise mean vector
    Eigen::MatrixXd invariant_key(_desc.rows(), 1);
    for ( int row_idx = 0; row_idx < _desc.rows(); row_idx++ )
        Eigen::MatrixXd curr_row = _desc.row(row_idx);
        invariant_key(row_idx, 0) = curr_row.mean();
    return invariant_key;

5.3.Sector-Key的生成函数，提取的是列向量的均值：

MatrixXd SCManager::makeSectorkeyFromScancontext( Eigen::MatrixXd &_desc )
     * summary: columnwise mean vector
    Eigen::MatrixXd variant_key(1, _desc.cols());
    for ( int col_idx = 0; col_idx < _desc.cols(); col_idx++ )
        Eigen::MatrixXd curr_col = _desc.col(col_idx);
        variant_key(0, col_idx) = curr_col.mean();
    return variant_key;

5.4.计算两个Scan-Context的距离(相似度)的函数：

使用Sector-Key进行加速计算，此处与论文中的不同;

std::pair<double, int> SCManager::distanceBtnScanContext( MatrixXd &_sc1, MatrixXd &_sc2 )
    // 1. fast align using variant key (not in original IROS18)
    MatrixXd vkey_sc1 = makeSectorkeyFromScancontext( _sc1 );
    MatrixXd vkey_sc2 = makeSectorkeyFromScancontext( _sc2 );
    int argmin_vkey_shift = fastAlignUsingVkey( vkey_sc1, vkey_sc2 );
    const int SEARCH_RADIUS = round( 0.5 * SEARCH_RATIO * _sc1.cols() ); // a half of search range 
    std::vector<int> shift_idx_search_space { argmin_vkey_shift };
    for ( int ii = 1; ii < SEARCH_RADIUS + 1; ii++ )
        shift_idx_search_space.push_back( (argmin_vkey_shift + ii + _sc1.cols()) % _sc1.cols() );
        shift_idx_search_space.push_back( (argmin_vkey_shift - ii + _sc1.cols()) % _sc1.cols() );
    std::sort(shift_idx_search_space.begin(), shift_idx_search_space.end());
    // 2. fast columnwise diff 
    int argmin_shift = 0;
    double min_sc_dist = 10000000;
    for ( int num_shift: shift_idx_search_space )
        MatrixXd sc2_shifted = circshift(_sc2, num_shift);
        double cur_sc_dist = distDirectSC( _sc1, sc2_shifted );
        if( cur_sc_dist < min_sc_dist )
            argmin_shift = num_shift;
            min_sc_dist = cur_sc_dist;
    return make_pair(min_sc_dist, argmin_shift);

5.5.回环检测主函数：

std::pair<int, float> SCManager::detectLoopClosureID ( void )

5.5.1.使用kd-tree找候选Scan-Context：

nanoflann::KNNResultSet<float> knnsearch_result( NUM_CANDIDATES_FROM_TREE );
knnsearch_result.init( &candidate_indexes[0], &out_dists_sqr[0] );
polarcontext_tree_->index->findNeighbors( knnsearch_result, &curr_key[0] /* query */, nanoflann::SearchParams(10) );

5.5.2.计算候选Scan-Context的距离(相似度)，从中找到距离最近(相似度最高)的那个：

for ( int candidate_iter_idx = 0; candidate_iter_idx < NUM_CANDIDATES_FROM_TREE; candidate_iter_idx++ )
        MatrixXd polarcontext_candidate = polarcontexts_[ candidate_indexes[candidate_iter_idx] ];
        std::pair<double, int> sc_dist_result = distanceBtnScanContext( curr_desc, polarcontext_candidate ); 
        double candidate_dist = sc_dist_result.first;
        int candidate_align = sc_dist_result.second;
        if( candidate_dist < min_dist )
            min_dist = candidate_dist;
            nn_align = candidate_align;
            nn_idx = candidate_indexes[candidate_iter_idx];

5.5.3.回环判断，根据阈值判断是否检测到回环：

/* 
 * loop threshold check
if( min_dist < SC_DIST_THRES )
     loop_id = nn_idx; 
     // std::cout.precision(3); 
     cout << "[Loop found] Nearest distance: " << min_dist << " btn " << polarcontexts_.size()-1 << " and " << nn_idx << "." << endl;
     cout << "[Loop found] yaw diff: " << nn_align * PC_UNIT_SECTORANGLE << " deg." << endl;