MATLAB绘制平面填充图入门详解_matlab区域填充颜色

二、fill命令的简单用法

基于语法：
1）fill(x, y, ‘color’)
功能：以x为横坐标，y为纵坐标，绘制同色填充的区域图。
(1)如果(x,y)组成的图形式闭曲线，则用颜色color填充该闭区域；
(2)如果(x,y)组成的图形是曲线段，则填充以曲线段为上曲边，该曲线段的两个端点连城的直线为另外一条边，生成封闭区域，再用颜色color填充该区域；
(3)color可以是单一颜色，如r、g、b等，也可以是颜色矩阵，此时必须与x和y同维数。
2） fill(x1, y1, ‘color1’, x2, y2, ‘color2’, … )
功能：绘制多个填充区域图，其中以x1为横坐标，y1为纵坐标，围成一个闭区域（非封闭则自动补充曲线端点的连线，以构成闭区域），以x2为横坐标，y2为纵坐标，围成另一个闭区域，并分别用相应的颜色填充。

例1 ：绘制对称区间上正态分布概率密度曲线填充图
参考代码如下：

clear all
%绘制正态概率密度函数对应的填充图
x1 = [ -8 : 0.2 : 8 ];
y1 = 2 * exp( -( x1 ).^2 / 2 );
fill( x1, y1, 'b' )
hold on
%绘制非对称区间上正态概率密度函数对应的填充图
x2 = [ 1: 0.1 : 10 ];
y2 = -2 * exp( -( x2 - 2  ).^2 / 2 );
fill( x2, y2, 'r' )
title( ' fill demo ' )
运行结果：
 
 上面的图形也可以使用如下代码实现，也就是使用在fill中同时绘制两个图形。代码如下： 
clear all
x1 = [ -8 : 0.2 : 8 ];
y1 = 2 * exp( -( x1 ).^2 / 2 );
x2 = [ 1: 0.1 : 10 ];
y2 = -2 * exp( -( x2 - 2  ).^2 / 2 );
fill( x1, y1, 'b', x2, y2, 'r' )
title( ' fill demo ' )
例2： 使用颜色矩阵绘制填充图。
 参考代码如下： 
x3 = [ 1 : 0.5 : 5 ];
y3 = x3.^2;
c = [ randn(length(x3), 1) ];%颜色矩阵，可以根据自己的需要指定
fill( x3, y3, c )
hold on
y4 = -x3.^2;
fill( x3, y4, 'c' )%此处的c是青色
title( 'color matris fill demo' )
运行结果：
  
三、area命令的简单用法
 
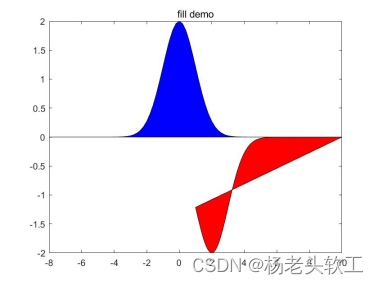
基本语法
 1）area(x, y, ‘name1’, value1, ‘name2’, value2, …)
 功能：绘制曲线段(x,y)与x轴围成封闭图形的同色填充的区域图。
 name的常用值如下：
 FaceColor：填充的颜色，其值必须是rgb格式的颜色数组
 EdgeColor:边缘线的颜色，其值必须是rgb格式的颜色数组
 FaceAlpha:透明度，其值是0~1之间的实数
 LineStyle:线元属性，即用什么样图元绘图，例如‘-’表示直线，‘:’表示虚线
 2）area(X)
 功能：X为矩阵，以 列 为单位绘制曲线，并用同色填充
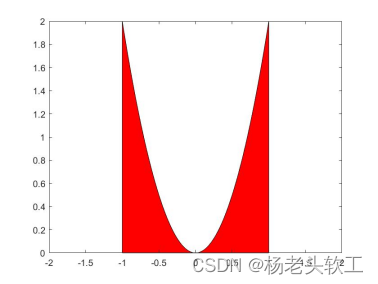
 例3：绘制曲线y=x^2在[-1,1]区间上的一段与x轴围成封闭图形的填充图。
 参考代码： 
clear all
x = [ -1 : 0.01 : 1 ];
y = x.^2 ;
area( x, 2*y, 'FaceColor', [ 1, 0, 0 ] )
axis( [ -2, 2, 0, 2 ] )
运行结果：
 
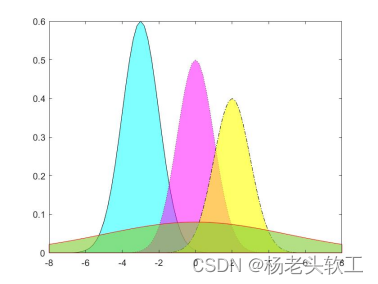
 例4：绘制正态概率密度函数曲线的填充图
 参考代码如下： 
clear all
x = [ -8 : 0.2 : 8 ];
y1 = 0.6 * exp( -(x+3).^2 / 2 );
area( x, y1, 'FaceColor', [ 0, 1, 1 ], 'FaceAlpha', 0.5 );   hold on
y2 = 0.5 * exp( -x.^2 / 2 );
area( x, y2, 'FaceColor', [ 1, 0, 1 ], 'LineStyle', ':', 'FaceAlpha', 0.5 );
y3 = 0.4 * exp( -(x-2).^2 / 2 );
area( x, y3, 'FaceColor', [ 1, 1, 0 ], 'LineStyle', '-.', 'FaceAlpha', 0.6 );
%也可以使用函数normpdf获取指定均值和方差的正态分布概率密度曲线上的纵坐标
y4 = 0.2 * normpdf( x/5, 0, 1 );
area( x, y4, 'FaceColor', [ 0.5, 0.8, 0.2 ], 'FaceAlpha', 0.6, 'EdgeColor', [ 1, 0, 0 ] );
运行结果：
 
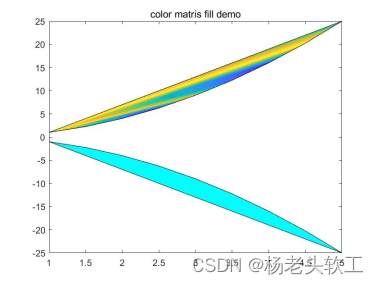
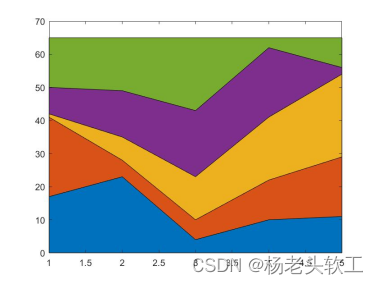
 例5：绘制5阶魔方矩阵的填充图
 参考代码如下： 
clear all
x = magic(5)
area( x )
运行结果：
 
				1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配
、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合
资源名：MATLAB绘制圆形并填充斜线_源程序代码_matlab
资源类型：matlab项目全套源码
源码说明： 全部项目源码都是经过测试校正后百分百成功运行的，如果您下载后不能运行可联系我进行指导或者更换。
适合人群：新手及有一定经验的开发人员
 用于填充图中选定区域的 Matlab 函数。 该函数的灵感来自 Python 库 Matplotlib 中的同名函数。
 该函数具有以下参数： 
 [y1handle, y2handle, h] = fill_between(x,y1,y2, where, opts);
x是 x 位置的向量
y1和y2是 y 位置的向量
where是指定填充y1和y2之间区域的条件的任何二进制向量。 这是一个很好的属性，因为我们可以绘制一条曲线，并决定只填充该曲线的特定区域（见下图左上角）。
 如果where=1或where=[]那么我们假设我们想要填充所有给定的 x 值（见右上角的例子）。
 y1和y2都可以是向量，在这种情况下，我们将在它们之间进行填充（参见右上角和左下角的示例）。
 y1或y2 （但不是两者）可以是常量，我们只是填充到特定的 y 基线，见右下示例。
				这篇文章的主要目的在于对colormap的解释，会涉及到fill和imshow的使用，因此首先解释fill和imshow的用法。fill的用法说明fill就是填充一个多边形区域。函数用法fill(x, y, colorspec)，x是多边形各点的x坐标，y是多边形各点的y坐标，colorspec就是颜色指定，有两种颜色指定的方法。例子1：x = [0, 0, 1, 1];
y = [0, 1, 1,
				编程渣的艰难探索之Matlab绘图
个人需求：用matlab绘制多条曲线并在指定不规则区域填色。
为什么一定要用Matlab呢？因为我觉得图形便于修改，看起来较为正规，代码量较少。
1 同时绘制多条曲线
1.1 基本代码（真的很基础）
x=0:0.005:5; %限定精度和范围（此处x在0到5之间取值，精度0.005）
y1=x; %函数表达式1
plot(x,y1,'black','k--','...
				要用MATLAB画平面网格填充图，可以使用函数meshgrid来生成网格数据，再利用函数surf或mesh来绘制填充图。
首先，我们需要定义x和y的取值范围，使用linspace函数可以生成一维数组来表示x和y的取值范围。例如，可以定义x为从-5到5的取值范围，y为从-3到3的取值范围。
然后，使用meshgrid函数生成x和y的二维坐标矩阵X和Y。这样，X和Y的大小将与x和y的取值范围相对应，生成的矩阵可以表示整个平面上的点坐标。
接下来，可以根据具体的要求定义z的取值范围，可以使用一些数学函数或者自定义函数来生成z的取值矩阵Z。例如，可以定义Z为x和y的某种函数关系。
最后，使用surf函数或mesh函数将生成的网格数据绘制出来。surf函数会根据网格数据的z值对平面进行填充，并可以通过设置颜色映射、透明度等参数进行样式设置。
具体的代码示例如下：
```matlab
x = linspace(-5, 5, 100);
y = linspace(-3, 3, 100);
[X, Y] = meshgrid(x, y);
Z = sin(X) + cos(Y);
surf(X, Y, Z);
上述代码将生成一个平面上的网格填充图，其中Z的取值是通过对X和Y的sin和cos函数的组合得到的。可以根据具体的需求和函数关系定义自己的Z值，从而绘制出相应的填充图。