关于时序数据稳定性的讨论

动机

在做时序数据预测时，时序数据是否稳定是预测结果最重要的指标之一。在这个方向属于计量经济学范畴，初学者经常由于缺乏相应基础而看不懂公式。本文会由浅入深解释其中涉及到的一些概念，并在最后结合 Dickey-Fuller / Augemented Dickey-Fuller Test 做下实际操作。由于统计学和计量经济学是比较复杂的课题，本文只会涉及到需要看懂 DF 算法的部分。

知识结构：

• Stationary & Non-Stationary
• Deterministic & Stochastic Trend
• Random Walk
• Unit Root Test
• Dickey Fuller Test

1 Stationary & Non-Stationary

考虑下面几幅图哪个符合平稳时序数据特征？

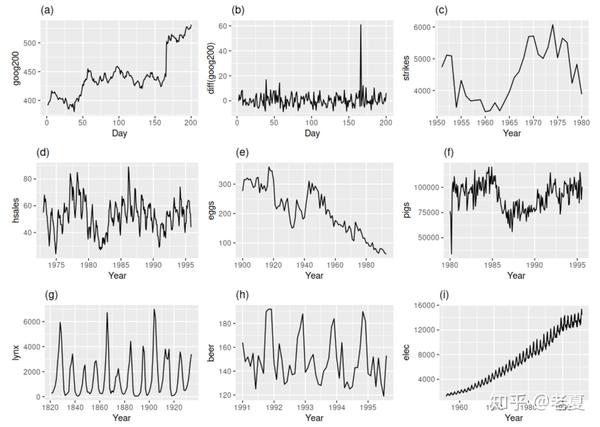
正确答案为 (b)、(g)。

Stationary 数据在时间序列上的表现是“一如既往”的平稳，在任何时间点上的观测到的数据应该都是近似的常数。

Non-Stationary 与其相反，往往会带有 趋势 或 周期性 的特点。

2 Non Stationary

Non-Stationary 数学上可满足如下特征：

• 非常数均值（Non-Constant in Mean）
• 非常数方差（Non-Constant in Variance）
• 上边两者结合

2.1 Non Constant in Mean

Non Constant in Mean 可分如下两种情况讨论：

• Deterministic Trend
• Stochastic Trend

2.1.1 Deterministic Trend

可确定趋势：指时序数据的趋势可以准确地用一个只以时间为变量的方程表达，如：

Y_t = \alpha + \beta t + \varepsilon_t 或者也可以简化为 Y_t = f(t)

满足如上特征的模型都可以称为 Trend Stationary Model 即，趋势稳定模型。为了证明其稳定的特性，可以使用时间轴上相邻两个数据的平均变化来衡量。

\Delta Y_t = Y_t - Y_{t-1} = \beta [ (t) - (t-1) ] + \varepsilon_t - \varepsilon_{t-1} 进一步简化成期望的形式：

\Delta E( \Delta Y_t ) = \beta

即：当变化的期望为常数时，尽管时序数据为趋势稳定，但仍然是 Non-Stationary。

2.1.2 Stochastic Trend

理解 Stochastic Trend 之前，首先要搞懂 Auto Regression（AR）是什么意思。这里不做深入讲解，大家可以粗略理解为在数据特征很少的时候，只能通过数值本身和数值在之前时刻的值来完成回归拟合。

AR(1) 指向前位移一位的 AR，公式可写成：

Y_t = \phi Y_{t-1} + \varepsilon_t ；其中 \phi 为前一时刻系数， \varepsilon_t 为 t 时刻的误差项

Random Walk 是 AR(1) 的特殊形式（后面会讲）

搞懂 AR 后，就可以用它来表达 Stochastic Trend 这种随机性强，不容易预测的趋势了。

假设我们使用 AR(1) Model，Non-Stationary, Stochastic Trend 可以用如下公式表达：

Y_t = C + \phi Y_{t-1} + \varepsilon_t 或 Y_t = f(Y_{t-1}) ； C 为公式的常数项

可以看出，AR(1) 模型中，当前值 Y_t ，只与其时序上前面一个值 Y_{t-1} 有关。

在做时序序列稳定性判断的时候这个公式很有用，我们可以说：

当 \left| \phi \right| < 1 时， 序列为稳定的

当 \left| \phi \right| \geq 1 时， 不稳定 （一般只讨论 等于 1 的情况，因为大于 1 在现实中尚未被发现）

假设 \left| \phi \right| = 1 ，我们对公式 Y_t = C + \phi Y_{t-1} + \varepsilon_t 可以做进一步的整理：

因为 Y_{t-1} = C + Y_{t-2} + \varepsilon_{t-1}

所以原公式可表示成 Y_t = C + (C + Y_{t-2} + \varepsilon_{t-1}) + \varepsilon_t

进一步整理为： Y_t = t C + Y_0 + \sum_{i=1}^{t}{ \varepsilon_i }

这种类型也称之为 Random Walk with Drift ，如果常数项 C 为 0，则称其为 Random Walk 。正是因为股价满足这种带偏移的随机游走，所以这种时序数据本身不存在任何 Pattern，所以才很难被机器学习预测。

3 Random Walk Process

Random Walk Process 满足以下性质：

• 对当前值 Y_t 值最好的预测前提是已知其时序上前面一个值 Y_{t-1}
• 均值为常数，方差为变量（所以不稳定）

4 Unit Root Test

该检测单位根的目的是为了计算出 \left| \phi \right| 是否为 1 （是否是 Randowm Walk)。

Unit Root 在一个系统中有如下特性：

• 如果系统是稳定的，那么由于突如其来的 Shock 对系统的影响会逐渐消失，即，系统会随时间推移重新回到之前的稳定状态
• 如果系统是不稳定的，Shock 的影响是 Permanent 的，在 \left| \phi \right| > 1 时，其影响是爆炸性的（现实中不存在，不需要特殊考虑）。

5 Dickey Fuller Test

为了检测一个序列是否存在单位根（Unit Root）可以使用 Dickey Fuller 检测。

或者说，可以检测一个序列是否是 Random Walk

以 AR(1) 为例，这个检测的函数表示为：

Y_t = \theta_0 + \phi Y_{t-1} + \varepsilon_t ；满足 \varepsilon_t \sim WN(0, \sigma_{\varepsilon}^{2})

如果 \phi \geq 1 那么可判定，该序列为不平稳时序序列，所以也无法有效的建模预测。

所以 DF 的假设可以总结为：

H_0 : \left| \phi \right| = 1 \Rightarrow Y_t \sim I(1) Non-Stationary

H_1 : \left| \phi \right| < 1 \Rightarrow Y_t \sim I(0) Stationary

为了计算相邻时序的演化过程，可以将上述表达式做进一步整理，设：

Y_t - Y_{t-1} = \theta_0 - (1-\phi)Y_{t-1} + \varepsilon_t

进一步得出： \Delta Y_t = \theta_0 + \delta Y_{t-1} + \epsilon_t

如果 \delta = 0 ，则存在单位根，即：

H_0 : \delta = 0

H_1 : \delta < 0

Dickey Fuller Test 一般可以分为以下三种类型讨论：

\Delta Y_t = \delta Y_{t-1} + \epsilon_t -> Random Walk

\Delta Y_t = \theta_0 + \delta Y_{t-1} + \epsilon_t -> Random Walk with Drift

\Delta Y_t = \theta_0 + \theta_1 t + \delta Y_{t-1} + \epsilon_t -> add drift and a linear time trend （ \theta_1 t 为 deterministic time component）

有了上面公式就可以判断当前序列是否是 Non-Stationary 或者是否存在 Unit Root（ \delta = 0 ），在这里可以使用 t-statistic on \hat{\delta} term 检验。

Dickey Fuller 已经给出了一个关于 \delta 的最小二乘的表（DF Table），我们只需要用 t-statistic 值对比这个表中的数值，就可以知道该时序数据是否存在 Unit Root。这个表中数值的分布也被称之为 Dickey-Fuller-Distribution； 如果 t-statistic 值小于 Dickey-Fuller-Distribution 中某个置信区间的值，则该时序数据为平稳的。

6 Augmented Dickey Fuller Test

因为普通 Dickey Fuller Test 建立在 AR(1) 上，所以我们对考虑多个 lag 位移的时候公式就不成立了。在这个基础上就有了这个加强版的 DF Test。

原公式为：

\Delta Y_t = \alpha + \delta Y_{t-1} + \epsilon_t

在存在多个 lag 中以 AR(2) 为例，只需要给当前的公式加一个 lagged delta term： \Delta Y_t = \alpha + \delta Y_{t-1} + \beta \Delta Y_{t-1}+ \epsilon_t

判别是否存在单位根的条件与之前的保持不变，依然是关于 \delta 的判断。基于这个公式可以推导出 high-order-process 的公式：

\Delta Y_t = \alpha + \delta Y_{t-1} + \sum_{i=1}^{h}{\beta_i \Delta Y_{t-i}} + \epsilon_t ；其中 \epsilon_t 不可以存在 serie correlation

同样如果 \delta = 0 ，则存在单位根，即：

H_0 : \delta = 0 -> Non-Stationary

H_1 : \delta < 0 -> Stationary

7 检验实现

DF / ADF 测试中：

• Hypothesis 分为 Null Hypothesis（Non-Stationary) 和 Alternate Hypothesis (Stationary)
• 如果 ADF Statistic < Critical Value 则 Null Hypothesis 这个假设不成立，即满足 Stationary
• 如果 ADF Statistic > Critical Value 则 Failed to reject Null Hypothesis 假设，所以为 Non-Stationary

代码上：

可以使用 Python 的 statsmodels 库中 statsmodels.tsa.stattools.adfuller 这个包。将序列传入这个方法后会返回几指标，其中两个重要的指标：ADF Statistics， 和 Critical Values（包括 1%, 5%, 10% 的置信区间）是我们判断是否存在单位根需要的。

通常会选用 Critical Values 中 5% 置信区间。比如：如果 DF 结果为 -1.7，5% 对应的值为 -2.4 则为 Non-Stationary 的序列。

结论：

啰嗦了这么多，只想说：

对于股票价格这种等同于随机游走的时序数据没必要尝试用机器学习建模预测啦！但是可以考虑用协整的方法做策略。