一、纹理运用
对纹理的理解:可以不单单看做是图像,而是一个记录了信息的存储块,可以通过位置查询各种信息。因此我们在后面可以看到,纹理它不仅仅可以记录颜色,还可以记录偏移、记录法向等等。
1. 环境映射
纹理记录各个方向来的光照信息。

2. 立方体映射

3.凹凸贴图
纹理指明对应点的高度偏移值。

点的高度发生变化会导致点的法线发生变化,从而影响着色效果。
如何计算改变后的法线呢?
在此之前我们先介绍下法线贴图,与凹凸贴图不同,法线贴图直接记录的法线,而凹凸贴图记录的高度,需要经过一次变换才能得到法线。因此介绍法线贴图有助于我们更好的理解凹凸贴图。
3.1 法线贴图
法线贴图直接记录的法线,我们知道法线的三个分量的范围是【-1,1】,而纹理贴图中记录颜色值范围是【0,1】。因此从纹理信息到法线信息需要做一个变换
normal = rgb * 2 - 1.0
法线贴图中记录的法线分别 物体空间的法线 和 切线空间的法线 ,它们之间有何区别?举个例子,如果当前法线贴图记录的是物体空间,所有的法线方向是(0,0,1),法线贴图作用于一个平行于XOY平面的矩形。则我们可以看到正确的效果,如下图显示:

但是当我们对这个矩形进行旋转和平移等其他操作。比如将它旋转到与平面XOZ平行时,效果如下:
此时从法线贴图中获取的纹理坐标仍然指向(0,0,1)即Z轴方向,而我们希望法线能指向正确的(0,1,0)即Y轴方向。
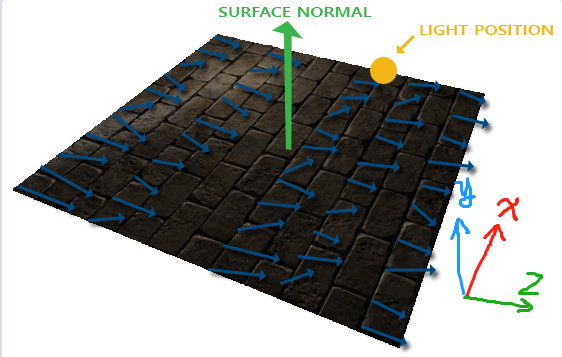

因此物体空间中的法线贴图,其缺点在于对物体进行旋转或者其他仿射变换后,其法线不再适用。因此引入切线空间法线贴图的概念。
切线空间可以这样理解:对于每个面,我们都可以定义其切线空间。其中该面的法线N的方向即为切线空间中的Z方向。法线贴图中的法线定义在该面的切线空间中,经过切线空间坐标系代表的矩阵变化后就可以将切线空间中的法线变换到物体空间。
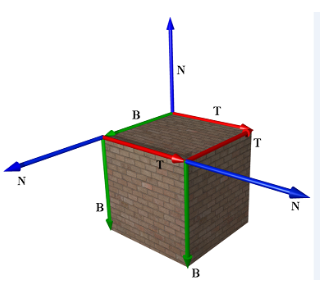
我们已知原法线N代表着切线空间的N,因此我们需要计算的是切线空间中的X.Y,也就是图中所表示的T, B。
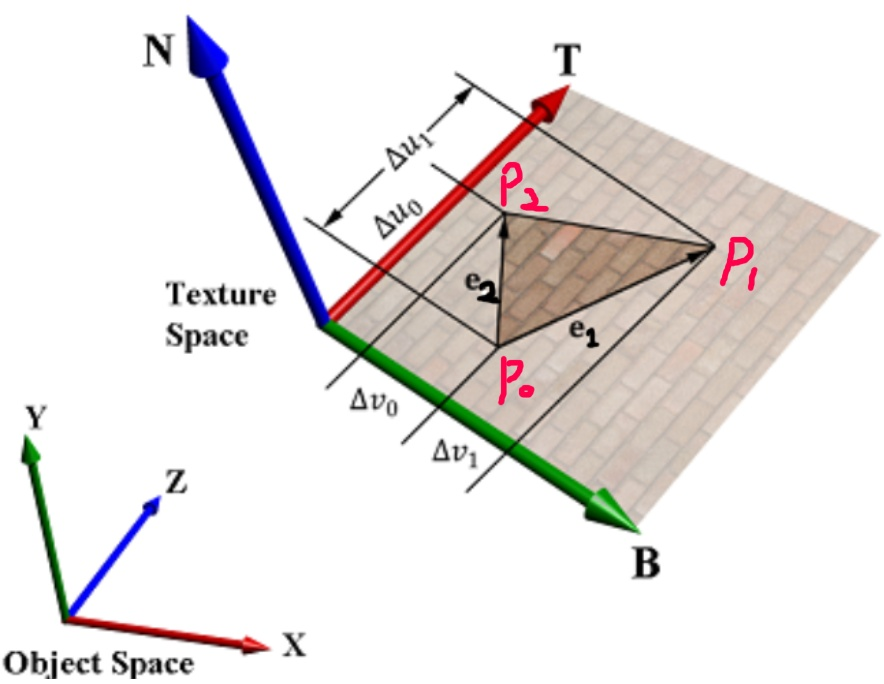
以三角形为例,我们知道三角形三个顶点P0, P1, P2,知道三个顶点的uv坐标(u0,v0)(u1, v1), (u2, v2)则我们可以列出如下式子:
p0 - p1 = (u0 - u1)T + (v0 - v1)B
p0 - p2 = (u0 - u2)T + (v0 - v2)B
设
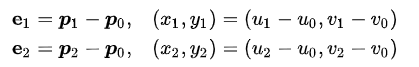
则
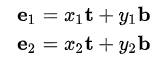
写成矩阵形式则为
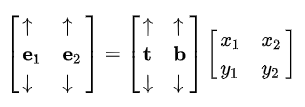
最后求T B即两边同乘上一个逆矩阵即可:
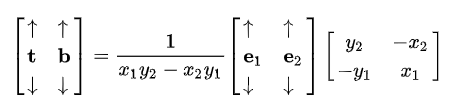
至此我们求得了面的切线空间的矩阵表示法【T, B , N】
法线贴图中法线由切线空间变换到物体空间则这样计算
【T, B, N】 * normal
以上我们是根据一个三角面的切线空间,结合法线贴图计算面的法线。而通常在shader编程中,我们只赋值顶点属性,那么如果计算点的切线空间呢。
在前几节中,我们计算顶点法线有一种方法,是加权平均该顶点组成的所有面的法线。切线空间也一样。平均该顶点组成的面的所有切线空间,可以得到顶点切线空间。
参考:
1.计算机图形学八:纹理映射的应用(法线贴图,凹凸贴图与阴影贴图等相关应用的原理详解) https://zhuanlan.zhihu.com/p/144357517
2.法线贴图那些事儿 https://www.cnblogs.com/bzyzhang/p/12954603.html3. 法线贴图 https://learnopengl-cn.github.io/05%20Advanced%20Lighting/04%20Normal%20Mapping/
3.2 凹凸贴图
凹凸贴图本质上与法线贴图类似,只不过凹凸贴图记录的是高度偏移,需要将高度偏移映射为切线空间中的法线,然后在用法线贴图那一套流程。
凹凸贴图中法线的计算可以通过纹理高度变化的快慢(导数)来求得。

首先我们考虑二维的情况,几何只有X,Y,纹理是一维的。
如下图所示,这段曲线代表纹理记录值随X变化的变化。我们知道物体空间中某一点的纹理对应着图中纹理上的P点,则通过P点和其附近的纹理值,我们可以得到P处的导数(也就是切线方向),而法线很简单,就是切线的X,Y颠倒,Y再加上一个负数。如下图所示:

然后我们再考虑三维情况
与二维类似,我们可以计算U V两个方向的导数,然后构造处切线空间法线。

至此我们可以法线,凹凸贴图本质上并没有改变点的位置,只是改变了点的法线从而实现凹凸的效果。它的缺点在于,物体边缘处和阴影边缘处可以看出物体本质上其实没有凹凸。

4. 位移贴图
位移贴图本质上改变了顶点的坐标。

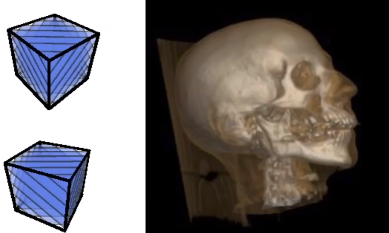
5. 3D纹理
空间中任何一个点都可以取到信息。常用于体绘制。
6.阴影贴图
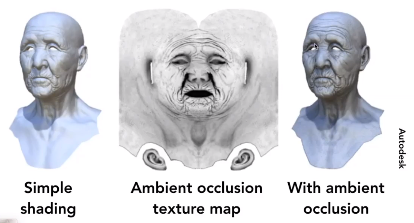
二、几何
1.几何的表示方法
1.1 隐式几何
描述几何上左右点满足的一个特定关系(函数),并不给定实际的一系列点。比如X^2 + Y^2 + Z^2 = 1这就是单位球的隐式表示。
隐式表示的优点:方便判断给定的任意一点是否在几何上。
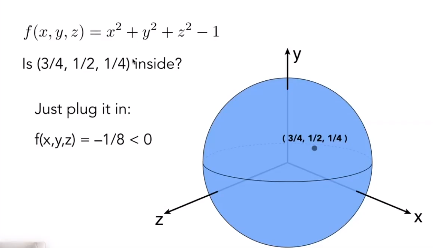
隐式表示的缺点:不知道具体哪些点在几何上,不知道几何的具体形状。
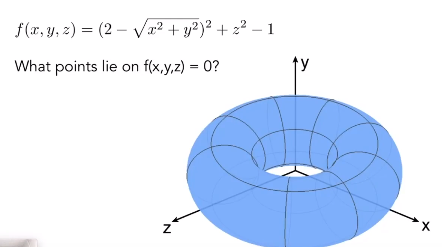
1.2 显式表示
比方说表示一个三角形,即给定三角形的三个顶点。这就是显示的表示方法。
另一种显示的表示方法:通过参数映射的方法定义表面
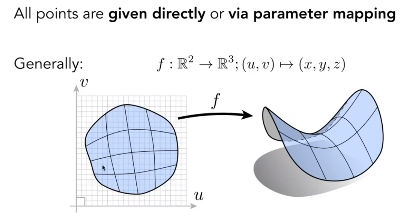
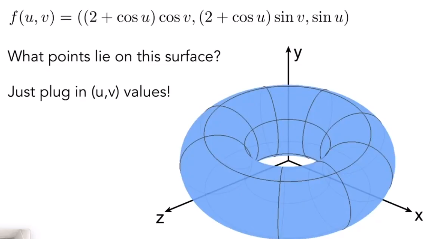
显示表示的缺点:无法方便的判断任意一个点是否在几何上
2.其他的隐式表示方式
2.1 CSG Constructive Solid Geometry
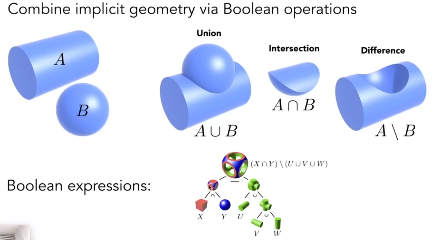
2.2 Distance Functions

2.3 Fractals 分形
