1. 引言
上一节我们讲完了各种激励函数的优缺点和选择,以及网络的大小以及正则化对神经网络的影响。这一节我们讲一讲输入数据预处理、正则化以及损失函数设定的一些事情。
2. 数据与网络的设定
前一节提到前向计算涉及到的组件(主要是神经元)设定。神经网络结构和参数设定完毕之后,我们就得到得分函数/score function(忘记的同学们可以翻看一下之前的
博文
),总体说来,一个完整的神经网络就是在不断地进行线性映射(权重和input的内积)和非线性映射(部分激励函数作用)的过程。这一节我们会展开来讲讲
数据预处理
,
权重初始化
和
损失函数
的事情。
2.1 数据预处理
在卷积神经网处理图像问题的时候,图像数据有3种常见的预处理可能会用到,如下。我们假定数据表示成矩阵为
X
,其中我们假定
X
是[N*D]维矩阵(N是样本数据量,D为单张图片的数据向量长度)。
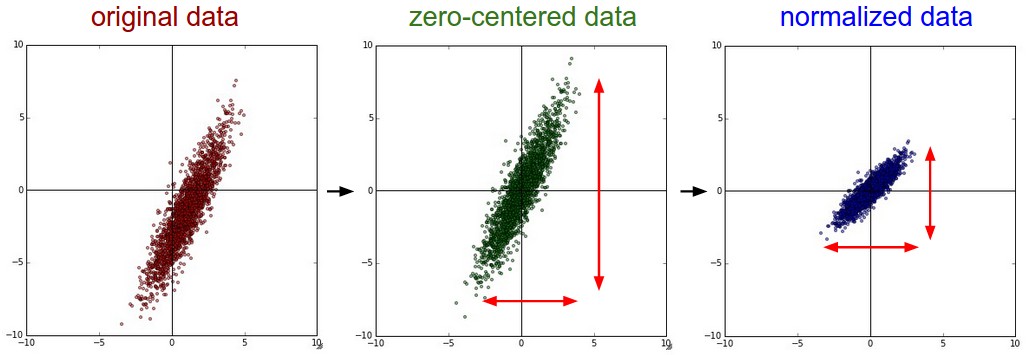
去均值
,这是最常见的图片数据预处理,简单说来,它做的事情就是,对待训练的每一张图片的特征,都减去全部训练集图片的特征均值,这么做的直观意义就是,我们把输入数据各个维度的数据都中心化到0了。使用python的numpy工具包,这一步可以用
X -= np.mean(X, axis = 0)
轻松实现。当然,其实这里也有不同的做法:简单一点,我们可以直接求出所有像素的均值,然后每个像素点都减掉这个相同的值;稍微优化一下,我们可以在RGB三个颜色通道分别做这件事。
归一化
,归一化的直观理解含义是,我们做一些工作去保证所有的维度上数据都在一个变化幅度上。通常我们有两种方法来实现归一化。一个是在数据都去均值之后,每个维度上的数据都除以这个维度上数据的标准差(
X /= np.std(X, axis = 0)
)。另外一种方式是我们除以数据绝对值最大值,以保证所有的数据归一化后都在-1到1之间。多说一句,其实在任何你觉得各维度幅度变化非常大的数据集上,你都可以考虑归一化处理。不过对于图像而言,其实这一步反倒可做可不做,因为大家都知道,像素的值变化区间都在[0,255]之间,所以其实图像输入数据天生幅度就是一致的。
上述两个操作对于数据的作用,画成示意图,如下:
PCA和白化/whitening
,这是另外一种形式的数据预处理。在经过去均值操作之后,我们可以计算数据的协方差矩阵,从而可以知道数据各个维度之间的相关性,简单示例代码如下:
X -= np.mean(X, axis = 0)
cov = np.dot(X.T, X) / X.shape[0]
得到的结果矩阵中元素(i,j)表示原始数据中,第i维和第j维之间的相关性。有意思的是,其实协方差矩阵的对角线包含了每个维度的变化幅度。另外,我们都知道协方差矩阵是对称的,我们可以在其上做矩阵奇异值分解(SVD factorization):
U,S,V = np.linalg.svd(cov)
其中U为特征向量,我们如果相对原始数据(去均值之后)做去相关操作,只需要进行如下运算:
Xrot = np.dot(X, U)
这么理解一下可能更好,U是一组正交基向量。所以我们可以看做把原始数据
X
投射到这组维度保持不变的正交基底上,从而也就完成了对原始数据的去相关。如果去相关之后你再求一下
Xrot
的协方差矩阵,你会发现这时候的协方差矩阵是一个对角矩阵了。而numpy中的
np.linalg.svd
更好的一个特性是,它返回的U是对特征值排序过的,这也就意味着,我们可以用它进行降维操作。我们可以只取top的一些特征向量,然后做和原始数据做矩阵乘法,这个时候既降维减少了计算量,同时又保存下了绝大多数的原始数据信息,这就是所谓的
主成分分析/PCA
:
Xrot_reduced = np.dot(X, U[:,:100])
这个操作之后,我们把原始数据集矩阵从[N*D]降维到[N*100],保存了前100个能包含绝大多数数据信息的维度。实际应用中,你在PCA降维之后的数据集上,做各种机器学习的训练,在节省空间和时间的前提下,依旧能有很好的训练准确度。
最后我们再提一下
whitening
操作。所谓whitening,就是把各个特征轴上的数据除以对应特征值,从而达到在每个特征轴上都归一化幅度的结果。whitening变换的几何意义和理解是,如果输入的数据是多变量高斯,那whitening之后的 数据是一个均值为0而不同方差的高斯矩阵。这一步简单代码实现如下:
Xwhite = Xrot / np.sqrt(S + 1e-5)
提个醒:whitening操作会有严重化噪声的可能。注意到我们在上述代码中,分母的部分加入了一个很小的数1e-5,以防止出现除以0的情况。但是数据中的噪声部分可能会因whitening操作而变大,因为这个操作的本质是把输入的每个维度都拉到差不多的幅度,那么本不相关的有微弱幅度变化的噪声维度,也被拉到了和其他维度同样的幅度。当然,我们适当提高分母中的安全因子(1e-5)可以在一定程度上缓解这个问题。
下图为原始数据到
去相关
到
白化
之后的数据分布示意图:
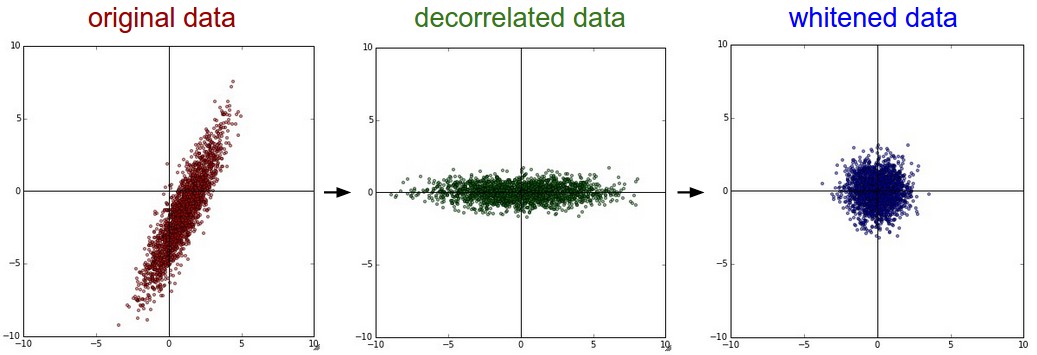
我们来看看真实数据集上的操作与得到的结果,也许能对这些过程有更清晰一些的认识。大家都还记得CIFAR-10图像数据集吧。训练集大小为50000*3072,也就是说,每张图片都被展成一个3072维度的列向量了。然后我们对原始50000*3072数据矩阵做SVD分解,进行上述一些操作,再可视化一下,得到的结果示意图如下:
我们稍加解释一下,最左边是49张原始图片;左起第2幅图是最3072个特征向量中最top的144个,这144个特征向量包含了绝大多数数据变量信息,而其实它们代表的是图片中低频的信息;左起第3幅图表示PCA降维操作之后的49张图片,使用上面求得的144个特征向量。我们可以观察到图片好像被蒙上了一层东西一样,模糊化了,这也就表明了我们的top144个特征向量捕捉到的都是图像的低频信息,不过我们发现图像的绝大多数信息确实被保留下来了;最右图是whitening的144个数通过乘以
U.transpose()[:144,:]
还原回图片的样子,有趣的是,我们发现,现在低频信息基本都被滤掉了,剩下一些高频信息被放大呈现。
实际工程中
,因为这个部分讲到数据预处理,我们就把基本的几种数据预处理都讲了一遍,但实际卷积神经网中,我们并没有用到去相关和whitening操作。当然,去均值是非常非常重要的,而每个像素维度的归一化也是常用的操作。
特别说明
,需要特别说明的一点是,上述的预处理操作,
一定都是在训练集上先预算的,然后应用在交叉验证/测试集上的
。举个例子,有些同学会先把所有的图片放一起,求均值,然后减掉均值,再把这份数据分作训练集和测试集,这是不对的亲!!!
2.2 权重初始化
我们之前已经看过一个完整的神经网络,是怎么样通过神经元和连接搭建起来的,以及如何对数据做预处理。在训练神经网络之前,我们还有一个任务要做,那就是初始化参数。
错误的想法:全部初始化为0
,有些同学说,那既然要训练和收敛嘛,初始值就随便设定,简单一点就全设为0好了。亲,这样是绝对不行的!!!为啥呢?我们在神经网络训练完成之前,是不可能预知神经网络最后的权重具体结果的,但是根据我们归一化后的数据,我们可以假定,大概有半数左右的权重是正数,而另外的半数是负数。但设定全部初始权重都为0的结果是,网络中每个神经元都计算出一样的结果,然后在反向传播中有一样的梯度结果,因此迭代之后的变化情况也都一样,这意味着这个神经网络的权重没有办法差异化,也就没有办法学习到东西。
很小的随机数
,其实我们依旧希望初始的权重是较小的数,趋于0,但是就像我们刚刚讨论过的一样,不要真的是0。综合上述想法,在实际场景中,我们通常会把初始权重设定为非常小的数字,然后正负尽量一半一半。这样,初始的时候权重都是不一样的很小随机数,然后迭代过程中不会再出现迭代一致的情况。举个例子,我们可能可以这样初始化一个权重矩阵
W=0.0001*np.random.randn(D,H)
。这个初始化的过程,使得每个神经元的权重向量初始化为多维高斯中的随机采样向量,所以神经元的初始权重值指向空间中的随机方向。
特别说明
:其实不一定更小的初始值会比大值有更好的效果。我们这么想,一个有着非常小的权重的神经网络在后向传播过程中,回传的梯度也是非常小的。这样回传的”信号”流会相对也较弱,对于层数非常多的深度神经网络,这也是一个问题,回传到最前的迭代梯度已经很小了。
方差归一化
,上面提到的建议有一个小问题,对于随机初始化的神经元参数下的输出,其分布的方差随着输入的数量,会增长。我们实际上可以通过除以总输入数目的平方根,归一化每个神经元的输出方差到1。也就是说,我们倾向于初始化神经元的权重向量为
w = np.random.randn(n) / sqrt(n)
,其中n为输入数。
我们从数学的角度,简单解释一下,为什么上述操作可以归一化方差。考虑在激励函数之前的权重w与输入x的内积
s
=
∑
n
i
w
i
x
i
部分,我们计算一下
s
的方差:
二、
损失
函数
中的正则项
1.正则化的概念:
机器学习中都会看到
损失
函数
之后会添加一个额外项,常用的额外项一般有2种,L1正则化和L2正则化。L1和L2可以看做是
损失
函数
的惩罚项,所谓惩罚项是指对
损失
函数
中某些参数做一些限制,以降低模型的复杂度。
L1正则化通过稀疏...
⾸先导⼊torch,注意虽然它被称为PyTorch,但是代码中使⽤torch⽽不是pytorch。n维数组,也称为张量(tensor),表示⼀个由数值组成的数组,这个数组可能有多个维度。具有⼀个轴的张量对应数学上的向量(vector);具有两个轴的张量对应数学上的矩阵(matrix);具有两个轴以上的张量没有特殊的数学名称。首先,使用arange创建一个行向量x。这个行向量包含以0开始的前12个整数,它们默认创建为整数。也可指定创建类型为浮点数。张量中的每个值都称为张量的元素(element)。
神经网络
中
损失
函数
后一般会加一个额外的正则项L1或L2,也成为L1范数和L2范数。正则项可以看做是
损失
函数
的惩罚项,用来对
损失
函数
中的系数做一些限制。正则化描述:L1正则化是指权值向量w中各个元素的绝对值之和;L2正则化是指权值向量w中各个元素的平方和然后再求平方根;一般都会在正则化项之前添加一个系数,这个系数需要用户设定,系数越大,正则化作用越明显。正则化作用:...
cnn网络中,网络更新一次参数是根据loss反向传播来,这个loss是一个batch_size的图像前向传播得到的loss和除以batch_size大小得到的平均loss。
softmax_loss前向传播中有这样一段代码: loss/get_normalizer(normalization_,valid_count),这就是对loss进行归一化。
如果我有ignore_label,val...
对
神经网络
输入做归一化/标准化处理。具体差别在后文展开。
如果不这样做,我们可以通过修改loss
函数
,增加一个惩罚值:pre-activation penalty
such as
klk_lkl是权重,根据情况进行调整。
The large pre-activation value of the neurons would
当我们进行机器学习时,需要将每一个样本经过模型得到一个预测值,这个预测值与真实值之间的差值我们就可以称之为
损失
,
损失
函数
就是为了测量这些
损失
的多少,以此来评估这个模型的好坏程度,即
损失
越小,模型越好,越接近实际。如果你还是不能理解
损失
函数
,那你可以这么理解:本博主很帅,你想变得和本博主一样帅,这时候你就需要一面镜子来衡量我们之间的差距,以便你追上本博主。这时,这面镜子就是
损失
函数
,用来衡量我们之间的差异,让你不断进行改变,越来越靠近本博主。
本文翻译自文章:Differences between L1 and L2 as Loss Function and Regularization,如有翻译不当之处,欢迎拍砖,谢谢~
在机器学习实践中,你也许需要在神秘的L1和L2中做出选择。通常的两个决策为:1) L1范数 vs L2范数 的
损失
函数
; 2) L1正则化 vs L2正则化。
作为
损失
函数
L1范数
损失
函数
,也...
1、正则化
(1)什么是正则化
正则化( Regularization )就是对最小化经验误差
函数
上加正则项约束,这样的约束可以解释为先验知识(有时候正则化参数等价于对参数引入先验分布)。约束有引导作用,在优化误差
函数
的时候倾向于选择满足约束的梯度减少的方向,使最终的解倾向于符合先验知识(如一般的 l-norm 先验,表示原问题更可能是比较简单的,这样的优化倾向于
1.
损失
函数
、代价
函数
与目标
函数
损失
函数
(Loss Function):是定义在单个样本上的,是指一个样本的误差。 代价
函数
(Cost Function):是定义在整个训练集上的,是所有样本误差的平均,也就是所有
损失
函数
值的平均。 目标
函数
(Object Function):是指最终需要优化的
函数
,一般来说是经验风险+结构风险,也就是(代价
函数
+正则化项)。
2. 常用的
损失
...