【C语言】数据储存 — 数据类型 —— 类型转换!
程序说到底就是对数据的处理,所以首先要弄清楚需要处理哪些数据,计算机如何存储这些数据。C语言根据需要,抽象出了一些基本数据类型和衍生数据类型。这些可以满足大部分需求,更复杂的抽象数据类型亦可通过它们来组成。
1. 数据存储
计算机存储的最小单位是bit,它表示0或1。而计算机 可寻址 的最小单位是byte,它至少由8个bit组成,内存就是由许多个byte组成并编址的。有OS时,C操作的是逻辑地址,OS会最终转为物理地址。
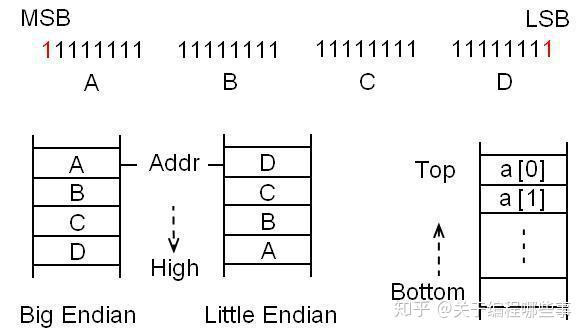
一个数据由多个bit组成,按照二进制的表示习惯,将最左侧的bit叫做 MSB (Most Significant Bit),最右侧的bit叫做 LSB (Least Significant Bit),这里的significant当然是指该bit表示的数量级。这些bit会划分到连续的byte中,存储时byte的顺序基于系统或平台。这又引出了 大小端 (Endian)的概念,LSB存储在高地址时叫Big Endian,否则叫Little Endian。但无论如何,该数据的地址都是指最低地址。而且进一步讲,数组和结构成员的地址也是按它们的指数或定义顺序向高地址增长的,即使在栈里也不例外(栈底一般在高地址,栈顶向低地址增长)。
C提供了关键字 sizeof 获取数据或类型占用内存的大小,结果以byte为单位。sizeof后如果跟括号,里面可以是类型或表达式,否则后面只能跟表达式。sizeof是运算符而不是函数,它的结果在编译时确定。如果操作对象是表达式,则返回其对应类型的大小,而不会执行表达式。对于想学习C/C++的小伙伴而言,学习的氛围和志同道合的伙伴很重要,笔者这里推荐一个C语言/C++编程爱好者的聚集地,直达→ C语言/C++编程学习进阶之路 !

计算机处理数据的单位叫 word ,我们一般说的32位64位计算机就是指word。为了提高处理效率,数据尽量不要或少跨word存储。这就需要数据的存储地址是数据长度的整数倍,和类型长度一样,对齐的单位一般是2的幂。基本类型对齐单位是其类型长度,组合类型(数组、结构、联合)的对齐单位是其成员的最大对齐单位。由于默认对齐的存在,组合类型的成员之间可能有一些空隙,sizeof的结果可能不是简单的累加了。但要注意,组合类型的成员总是尽量向低地址靠齐,所以组合类型的开头是不会有空隙的。

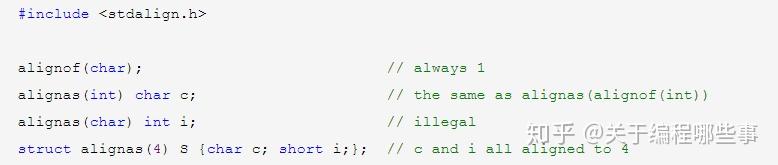
新规范中引入了关键字 _Alignof 和 _Alignas (同sizeof一样不是函数),新引入的关键字一般以'_'和大写字母开头(为了不和编译器的扩展或用户自定义冲突),如果想用小写字母开头的,需要include对应的标准库(宏定义)。_Alignof后跟类型,得到类型的对齐单位。_Alignas后跟类型或整数常量,用来修饰类型或变量定义,但它不能小于其原有的对齐单位。
C中数据一般叫 对象 (object),不同的数据会有不同的 类型 (type)。类型决定了数据的长度和格式,除此之外的类型属性(比如const)只有编译器能看到,而对计算机是透明的。C定义了char、int、float、double四种 基本型 ,还有两个特殊类型void和枚举,以及它们的 衍生 (derived)类型(指针、数组、结构、联合、函数)。基本型和枚举并称为 代数型 (arithmetic),代数型和指针并称为 度量型 (scalar),数组和结构并称为 聚合型 (aggregate)。 整型 (interger)包括char、int和枚举,浮点型包括float和double,整型和浮点型并称 实数型 (real)。新规范中还定义了可选关键字_Bool、_Complex和_Imaginary,个人认为可以当做基本型,而且_Bool可以划到整型里。
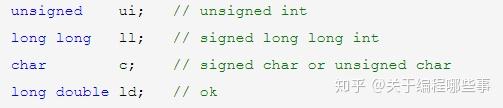
类型前可以有多种修饰符,它们有不同种类和用途,这里先介绍一类叫类型说明符(非规范定义)。包括short、long、long long(新规范)、signed和unsigned,它们仅作用于基本型,且长度和符号可以组合使用。所有的说明符都可以修饰int,int默认为signed(可不写),有说明符时int可不写。signed、unsigned可修饰char,long可修饰double,其它用法皆非法。
2. 数据类型
2.1 整型
整型数有不同的长度,其中char始终为1,int一般为字长,枚举与int一样,_Bool基于实现。short至少16bit且不超过int,long至少32bit且不低于int,long long至少64bit且不低于long。无符号整型的值即它的二进制数的值,有符号整型的值基于平台实现。少数老的平台采用的是反码表示法(1's complement),它概念简单直观,但却不方便计算,个人认为注定被淘汰,没有讨论价值。现在几乎所有的平台都使用 补码表示法 (2's complement),该模型更符合问题的本质,自然也更便于计算。对于负数,补码即0减去它的绝对值(有underflow),实现了正负数的平滑连接。
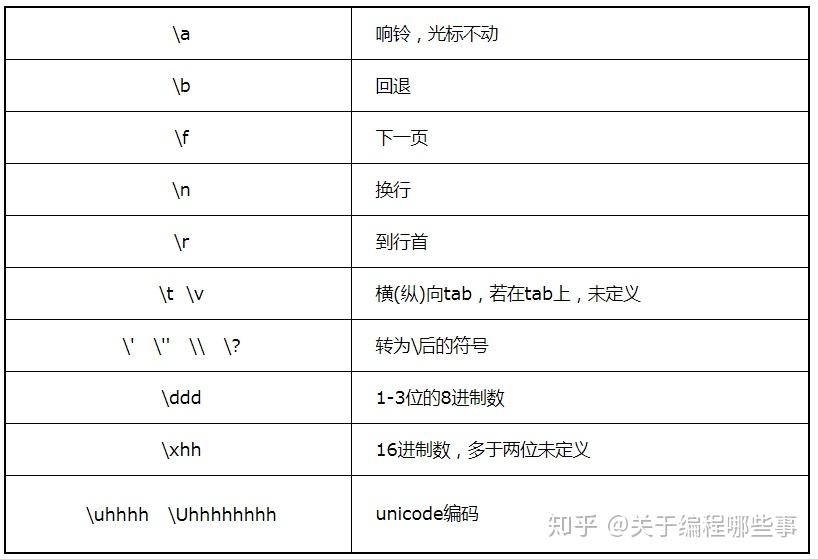
字符型 包含 char 、wchar_t、char16_t和char32_t,其中char是基本类型,其它为int(带说明符)的宏定义。char类型永远是1个byte,可表示basic字符集,它的符号是基于实现的。字符常量用一对单引号表示,引号里为字符或转义序列,引号前有可选前缀L、u和U(分别对应后3种字符型)。字符常量本身的类型为int或unsigned int,它的值为引号中字符的编码或转义序列的值。引号中可以有多个字符,但它们在int中的存储位置是不定义的。下表中列出了转义序列及其含义:
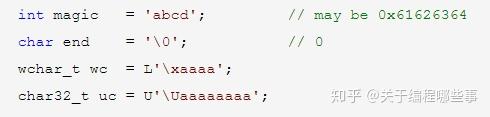
int型常量 以非0数字开头则表示10进制数,0x或0X开头表示16进制数,0开头表示8进制数。后面可以有后缀U、L或LL(不限大小写),分别表示unsigned、long和long long。U可以和L或LL组合,且顺序随意。int型可以按它能表示的最大数来排序,如果能表示的最大数相同,则按int、long、long long排序。一个可能的队列为int、long、unsigned int、unsigned long、long long、unsigned long long。int型常量的类型以后缀类型(默认为int)为起点,从队列中寻找第一个满足规则且能包含其值的类型。规则是:(1)如果起点为unsigned,则尝试signed;(2)如果起点为signed且为10进制数,则不尝试unsigned。另外要注意,不存在负常量,它只是对正常量的负运算。
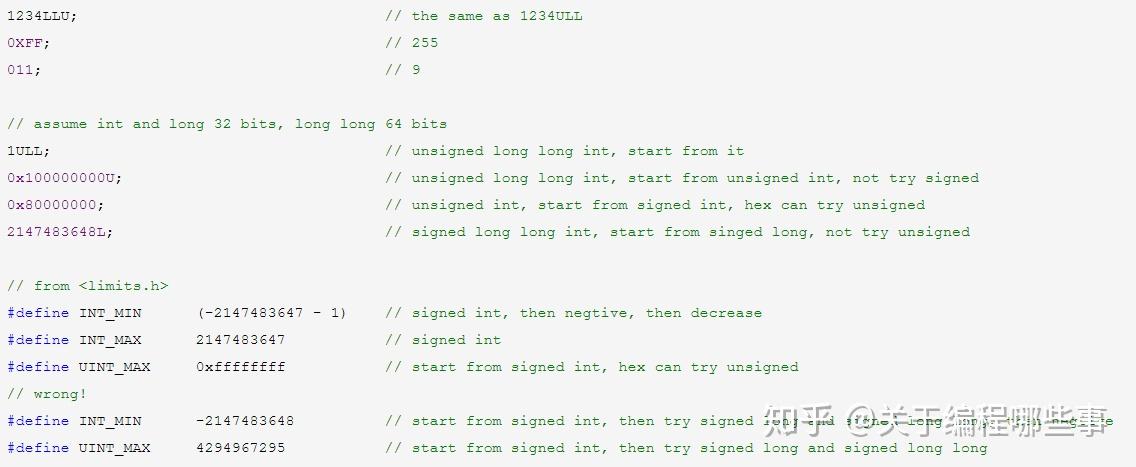
枚举 (enumeration)是一个特殊的自定义的类型,它为其每一个常量定义了名字,这些常量的值都是int型(可为负数)。枚举常量的值可以显式指明,或者为其前一常量加1,第1个常量的隐式值为0。枚举常量可以像宏一样使用,往往用于简单的编号。

2.2 浮点型
浮点型的计算机表示由平台决定,但几乎所有实现都遵循规范 IEC-60559(IEEE-754) ,这里简单介绍一下该规范中的浮点表示。根据数据长度(精度),规范将浮点分为single、double和double-extended,分别对应C中的 float、double 和long double。float和double的长度分别为32和64,long double未作明确定义。
从MSB到LSB,浮点型被分为符号位(sign,1位)、指数(exponent,8或11位)和尾数(fraction,23或52位),它可表示为以2为底的科学计数。
符号位是整个浮点数的符号,所以会存在正负0和正负无穷。指数被解释为无符号整数,并减去一个偏差(bias)。偏差值会导致emaxemax比eminemin绝对值大1(考虑到倒数的溢出),比如float类型的偏差为127,emaxemax = 128,eminemin = -127。指数取最大值时,若尾数为0,整个数解释为正负无穷大,否则为NaN(not a number)。指数为最小值时,尾数解释为0.f0.f(denormalized),否则解释为1.f1.f(normalized)。
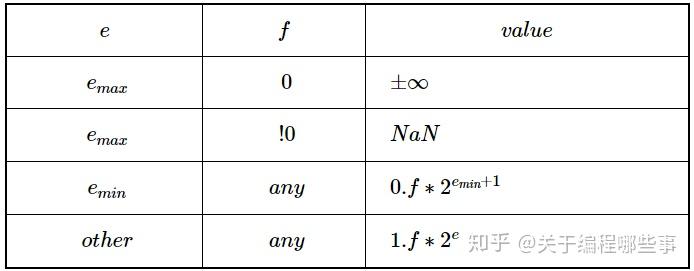
实数是连续的,无法用计算机精确表示,整个浮点数空间可以看做是实数的采样。对normalized区段,每个数量级的采样数是相等的(ff的每一位都有意义),对denormalized区段,每个数量级的采样数递减(ff的实际有效位)。denormalized区段指数采用的是emin+1emin+1,而非eminemin,保证了和normalized区段的平滑过渡,很是巧妙!浮点数也支持正负无穷和NaN这类抽象值,为错误处理提供了很好的工具。超出表示边界的值都是无穷大,无意义的数(0/00/0,0∗∞0∗∞)都表示为NaN,它们亦可参加运算,值视情况而定。浮点运算在运算时保持精度,但对结果进行舍入(每一个运算),舍入的方法是尾数为偶数(round to even)。

由于舍入或正负0的存在,和0的比较变得不可靠,所以不要判断某浮点数是否为0。在比较两个浮点数是否相等时,直接用a == b或a != b,不要将a - b与0比较。浮点的舍入会导致原本相近两个数的差被掩盖,有时调整算法可以减少 误差 ,读者可以思考以下公式变换带来的精度提高。

浮点常量 一般以10为底,新规范支持以2为底的浮点常量(0x开头),它可以避免精度的丢失。浮点常量的尾数部分不可少,10为底用10进制数,2为底用16进制数。尾数可以为整数或小数,若小数点前或后为0可不写,但不能同时不写。指数部分从字母e、E(10为底)或p(2为底)开始,后面都跟10进制数(为了和后缀中的F区分开来)。10为底的浮点常量可以没有指数部分,但这时尾数不能为整数,否则会被解析为整型。2为底的浮点常量必须有指数,否则后缀F无法与尾数区分。浮点常量默认为double,后缀F和L(不分大小写)分别表示float和long double,无类型提升(和常整型不同)。

新规范中支持复数(complex)和虚数(imaginary),但是可选功能。多数编译器是用结构来定义复数的,而不是用关键字 _Complex 和 _Imaginary 。复数和虚数必须由浮点型修饰,虚数常量ii是基于实现的。除ii外没有复数常量,是由浮点数的类型提升完成的。

2.3 组合类型
这里的组合类型非标准定义,它指数组、结构和联合(以后将结构和联合叫复合类型)。组合类型由多个成员组成,每个成员可以为除void和函数之外的任何一种类型。组合类型是表示复杂类型的重要工具,也是抽象类型的必要元素。
数组 由多个相同类型的成员组成,它们在内存中连续分布,可以通过index获取。C中没有多维数组的概念,只有数组的数组,仅此而已。数组的长度不能为0,新规范支持结构末尾的可变数组a[](flexible array member),它相当于预定了一个数组的位置,而不一定有成员。含可变数组的结构至少还有另外一个成员,且它不可以再做组合类型的成员。由于align的作用,可变数组与结构最后一个成员之间可能有空隙,该结构的sizeof结果包含该空隙。

字符串 是一类特殊的数组,它的成员是字符型。字符串常量定义在一对双引号中,其中可以是字符或转义序列,也可以有L、u或U作前缀。字符串常量中不能换行,但可以有空格或tab。连续的字符串常量(中间可有空白)在预处理时会被拼接为一个,该特点便于书写长字符串和分开转义序列与普通字符,单字节字符串和宽字节字符串拼接的结果为宽字符。字符串常量(拼接后)末尾有一个隐式的字符'\0',字符串函数把它当做结束符。任何字符串常量(包括初始化字符串)都会存储在常量区,编译器可以选择合并相同的字符串常量。字符串常量可以直接当数组使用,但对其修改是未定义的。

结构 体中可以包含不同类型的成员,由它可以组成更复杂的抽象类型。如果从面向对象的角度说,对象的属性体现在结构的普通成员上,对象之间的关系则体现在结构的指针成员上。结构中还可以定义位域(bit field),位域是指定长度的整型,它被放置在word中。空间足够时,相邻位域紧靠之前的位域,否则未定义。未做显式说明时,int位域的符号基于实现。对位域的操作效率比普通整型低,它往往用于紧凑空间或一致性需求(传输协议)。
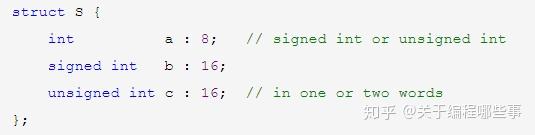
联合 也可以包含不同类型的成员,但它们的地址都是一样的(等于联合本身的地址),也就是说成员在内存里有重叠。联合中也可以有位域,它们也是互相重叠的。联合一般用于结构的分情况解释或数据的局部操作,后者的一个例子是大小端判断。
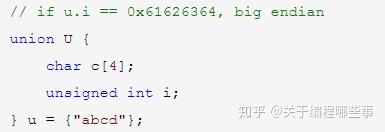
基本类型和字符串都有常量表示,新规范中还支持 复合常量 (compound literal),它的定义方法是类型后加初始化序列。但复合常量本质上是匿名变量,它和变量的性质几乎一样,唯一的差别是const的复合常量和字符串常量有一样的存储属性。

2.4 其它类型
void 严格来说不是一个类型,单独使用时表示“没有”,仅用于表示函数返回、函数参数和表达式。void指针仅表示数据地址,而无数据的类型信息,它取代了旧规范库中一些场合的char指针。
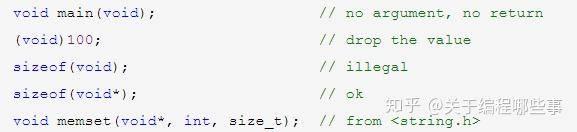
函数 也是一种对象,它的类型由返回类型和参数类型共同决定。而且函数可以看作const的,因为它在代码区,不可修改。
指针 即带有类型的地址,指针的长度是未定义的,但相同类型的指针长度是相同的。机器码中的变量使用地址表示的,所以指针变量只不过是地址的地址,无需多做探讨。如果说变量是对数据的一般化,则指针变量是对变量的一般化。这种更深层次的功能使得C更灵活更强大,但同时也更危险,因为它影响的不是某个数据。避免问题的关键就是一定要“指有所指”,未初始化的指针(dangling pointer)可能破坏任何数据。
空指针 是一个特殊的指针常量,它不等于任何有意义的地址,它无法直接表示。常量0在特定语境下表示空指针,但最终的编译结果未必是0。NULL大部分时候指空指针,宏NULL一定要定义成对0的强制转换,以避免0的多义性。

还有一类指针常量就是静态存储的变量的地址以及函数的地址,它们可以用于初始化静态存储的变量(必须用常量初始化,见下章)。

3. 类型转换
表达式中的操作符有时会引起操作数的 类型转换 (type conversion),本节对这类转换做一些总结。当新类型可以表示操作数时,转换后的值不变。任何度量类型转换为_Bool时,如果为0则转为0,否则转为1。向unsigned整型转换时,若操作数是整数则取模,若为浮点则去掉小数部分(整数部分若超出新类型则未定义),若为复数则先去掉虚部。向signed整型转换时,若操作数超出表示则未定义。向浮点数转换时,若无法精确表示则舍入方法未定义。向复数转换时,若操作数无虚部则结果虚部为0。
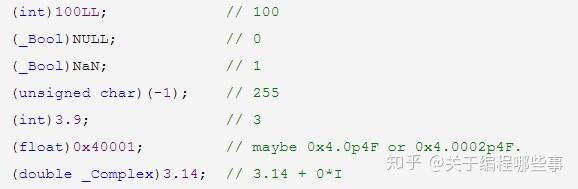
整型和指针可以互相转换,但结果是未定义的。指针之间的转换也可以,但align不一致时未定义。甚至不同类型的函数指针也可以转换,但无意义。指针转换并不改变所指向地址的内容,用新指针取值时数据将被重新解释。

除了显式的强制转换外,还会发生一些隐式的转换,尤其常见于代数运算中。 整型提升 (integer promotion)将小整型提升为int或unsigned int,若int包含该小整型则转为int,否则转为unsigned int。整型提升仅发生于前置+-、~和移位的所有操作数,以及switch语句和常用代数转换中。 常用代数转换 (usual arithmatic conversion)发生在比较、算术(+-*/%)和位(&|^)运算中,它将两个操作数转换为相同的类型:
(1)若操作数中有浮点数,则向最高精度浮点数转换。但整数无需做整型提升,实数无需向复数转换。
(2)若操作数中没有浮点数,则先做整型提升。提升后若一个类型包含另一个,则转换为较大范围者,否则转换为较大范围的无符号类型。

赋值操作、函数的参数传递和值返回也可以看做是隐式转换,当不知道函数参数的类型时,整型要做整型提升,float要转换为double( default argument promotion )。

另外还有两个重要的隐式类型转换必须弄清楚,就是 数组名和函数名 。数组名即表示整个数组,但在除sizeof、_Alignof和&作用下,数组名自动转换为首元素的指针。字符串常量在以上3种情况和用作为数组初始化之外,也自动转换为首元素的指针。函数名是函数类型,在除sizeof、_Alignof和&作用下,函数名自动转换为相应函数类型的指针。

“我是一名从事了10年开发的老程序员,最近我花了一些时间整理关于C语言、C++,自己有做的材料的整合,一个完整的学习C语言、C++的路线,学习材料和工具。对于想学习C/C++的小伙伴而言,学习的氛围和志同道合的伙伴很重要,笔者这里推荐一个C语言/C++编程爱好者的聚集地, 直达→ C语言/C++编程学习进阶之路 !欢迎初学和进阶中的小伙伴。希望你也能凭自己的努力,成为下一个优秀的程序员。工作需要、感兴趣、为了入行、转行需要学习C/C++的伙伴可以一起学习!”
关注我的专栏,带你遨游代码世界!
最后分享一张C/C++学习路线图给爱学习的小伙伴们


