一、基本概念

1. 参数检验 是 在总体分布形式已知的情况下，对总体分布的参数如均值、方差等进行推断的方法 。但是，在数据分析过程中，由于种种原因，我们往往无法对总体分布形态作简单假定，此时参数检验的方法就不再适用了。
2. 非参数检验 正是一类基于这种考虑， 在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法 。

	参数检验	非参数检验
检验指标	均值	中位数
总体分布情况	已知	未知
针对的对象	参数	分布情况
优点	符合条件时， 检验效率高	应用范围广、 简便、易掌握
缺点	对数据要求严格，要求数据 连续性、分布型已知 和 总体方差相等	若对 符合参数检验条件的数据用非参数检验，则检验效率低于参数检验

1. 参数检验 的集中趋势的衡量为 均值 ，而 非参数检验 更适合为 中位数 ，比如收入情况，如果在样本中加入几个亿万富翁，即使一般人的收入没有变化，平均值也会大幅度增加，但中位数没有显著差异。
2. 优缺点对比：1） 参数检验 ：优点是 符合条件时，检验效率高 ；其缺点是 对数据要求严格 ，如等级数据、非确定数据不能使用参数检验，而且要求数据的分布型已知和总体方差相等。
   2） 非参数检验 ：优点是 应用范围广 （没有正态分布的假设）、 简便、易掌握 ；缺点是 若对符合参数检验条件的数据用非参数检验，则检验效率低于参数检验 。如无效假设是正确的，非参数法与参数法一样好，但如果无效假设是错误的，则非参数检验效果较差。
3. 当 样本量足够大 时， 参数检验 的方法对非正态分布的数据也能够很好地进行处理，因为样本均值的分布根据中心极限定理是近似正态分布。当 样本量较小且分布未知 时，通常会考虑使用 非参数检验 。
4. 各类方法对比：

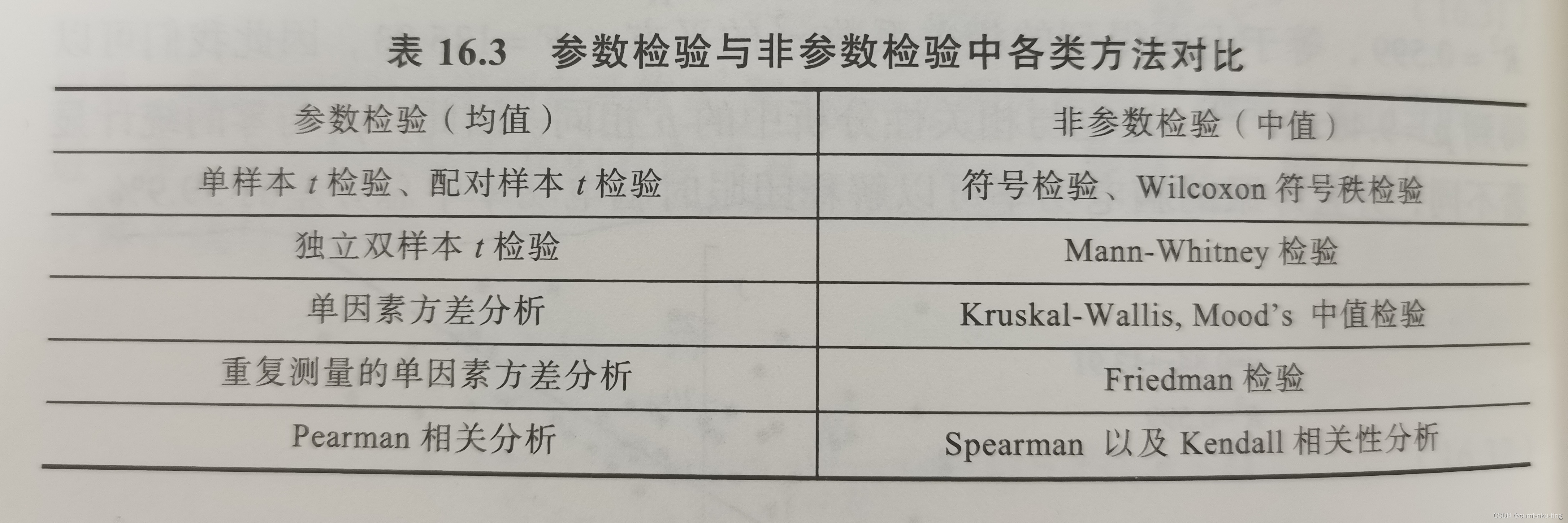
三、具体方法对比

1、参数检验

1. t检验 ：它适用于 计量数据、正态分布、方差具有齐性的两组间小样本比较 。包括样本与均数间、两样本均数间、配对数据间的比较三种，分别对应的是 单一样本t检验 ， 独立样本t检验 和 配对样本t检验 ，三者的计算公式是不同的。T检验需要满足正态分布性和方差齐性，在不满足方差齐性时，需要使用t‘检验。
2. U检验 ，也称Z检验，应用条件与t检验基本一致，只是当大样本(N>30)时用U检验，而小样本(N<30)时则用t检验。
3. 方差分析 ：用于 正态分布、方差齐性的多组间计量比较 。常见的有 单因素 、 双因素 、 多因素 的均数比较，“因素”指影响未知变量的行为（事件）。方差分析首先是比较各组间总的差异，如总差异有显著性，再进行组间的两两比较。

我们提到 不论是t检验还是方差分析必须满足两条假设，分别是正态性和方差齐性 。因此，在一个完整的统计工程中，必须首先检测数据的正态性和方差齐性，matlab里有对应的函数可以直接调用， lillietest正态检验函数 和 vartestn方差齐性检验 。

2、非参数检验

非参数检验我们一般用的不多，简单列举了几个，非参数检验检验的是分布而不是参数，所以总体分布是未知的。

1. 符号检验 ：符号检验还可用于 配对样本的比较检验 ，符号检验法是 通过两个相关样本的每对数据之差的符号进行检验，从而比较两个样本的显著性 。具体地讲，若两个样本差异不显著，正差值与负差值的个数应大致各占一半。
2. Wilcoxon符号秩检验 ：符号检验只考虑的分布在中位数两侧的样本数据的个数，并没有考虑中位数两侧数据分布的疏密程度，这就使得符号检验的结果比较粗糙，检验功率较低。统计学家维尔科克森在1945年，提出了一种更为精细的“符号秩检验法”，该方法是在配对样本的符号检验基础上发展起来的， 比传统的单独用正负号的检验更加有效 。它适用于 单个样本中位数的检验 ，也适用于 配对样本的比较检验 ，但并不要求样本之差服从正态分布，只 要求对称分布即可 。
3. 卡方检验 : 就是 统计样本的实际观测值与理论推断值之间的偏离程度 ，以卡方分布为基础，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合，若两个值完全相等时，卡方值就为0，表明理论值完全符合。
4. K-S检验 : 是基于累计分布函数的， 检验一个样本是否服从既定的分布 ，或者 检验两个样本是否来自同一个分布 。
5. 曼·惠特尼检验 ，是 比较两个独立样本的非参数检验 。
6. K-W检验 ，又称“H检验”，用以 检验两个以上样本是否来自同一个概率分布的一种非参数方法 。被检验的几个样本必须是独立的或不相关的。与此检验对等的参数检验是单因素方差分析，但与之不同的是，K-W检验不假设样本来自正态分布。它的原假设是各样本服从的概率分布具有相同的中位数。
7. Friedman 福里德曼检验 : 又被称之为 双因素秩方差分析 ，是 非参数版的anova2 。同anova2一样，待检验的数据也必须是均衡的。但是福里德曼检验和anova2检验不完全相同， anova2同时注意两个因素对待检验数据的影响 ，但是， 福里德曼检验只注重2个因素中的其中一个对待检验数据的影响，而另一个因素则是用来区分区组用的 。（有4名美食评委1234对来自于四个地区ABCD的厨子做的烤冷面做出评价打分，现在我们想知道，这四个地方的烤冷面品质是否相同，那么同一个评委对四个地区厨师的打分就具有可参考性，而不同地区评委之间对同一个厨师的打分参考性几乎没有（受评委自己的主观意识影响太强）。因此，我们只考虑地区因素，而评委因素是区组因素，不同区组之间的数据没有可比较性。）

1， 参数检验 是针对参数做的假设， 非参数检验 是针对总体分布情况做的假设，这个是区分 参数检验 和 非参数检验 的一个重要特征。 2，二者的根本区别在于 参数检验 要利用到总体的信息（总体分布、总体的一些参数特征如方差），以总体分布和样本信息对总体参数作出推断； 非参数检验 不需要利用总体的信息（总体分布、总体的一些参数特征如方差），以样本信息对总体分布作出推断。 3， 参数检验 ... 非参数检验 是针对总体分布情况做的假设，这是区分的一个重要特征； 2、根本区别在于， 参数检验 要利用到总体的信息（总体的分布、总体的一些参数特征，如方差），以总体分布和样本信息对总体参数做出推断； 非参数检验 不需要利用总体信息，以样本信息对总体分布做出推断； 3、正态分布用 参数检验 ，非正态分布用 非参数检验 。...