-
做的东西涉及一些指令的传输,很容易通过抓包获取指令内容,为了保证指令安全,需要对指令进行加密,决定自己实现一个基于Diffie-Hellman密钥协商算法的封装类
-
GitHub
1、通信双方通过协商,共同建立会话密钥,任何一个参与者均对结果产生影响,不需要任何第三方参与
2、会话密钥由每个协议参与者分别产生的参数通过计算得到
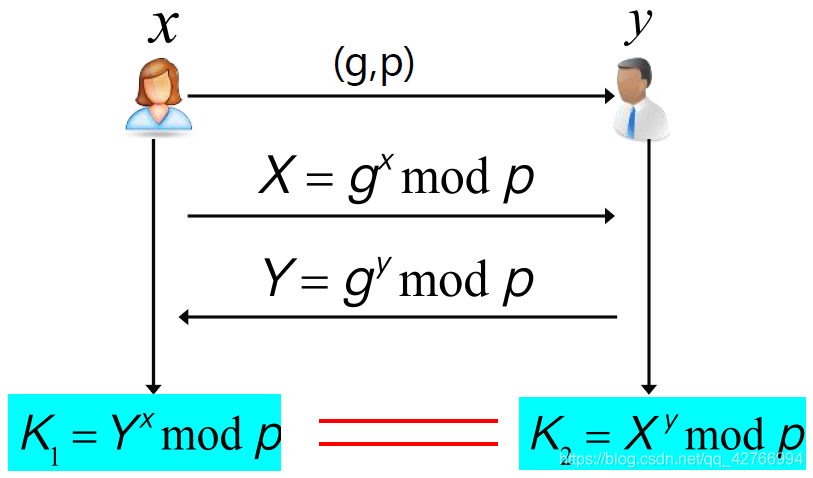
1、初始化:A选取一个生成元
g
和一个大素数
p
,发送给B
2、A随机选取0<
x
<p-1,计算
X
= g
x
mod p后,将X传给B
3、B随机选取0<
y
<p-1,计算
Y
= g
y
mod p后,将Y传给A
4、A计算Y
x
mod p得到会话密钥
K1
5、B计算X
y
mod p得到会话密钥
K2
6、由下可知 K1 == K2,此时双方便可利用会话密钥进行加密通信了

#ifndef CRYPTO_H
#define CRYPTO_H
#include <stdlib.h>
* 作者:公羽向阳
* 时间:20201025
* 编译器:TDM-GCC 4.8.1 64bit
* 基于DH的密钥协商加密类
* 1、请先使用Crypto::init()方法初始化随机种子
* 2、客户端构造此类,服务端通过客户端生成的 [g,p] 构造
* 3、客户端通过调用get_public()方法得到一个数组 [g, p]
* 4、客户端、服务端通过get_pub_key()方法获取公钥 C、S 用于协商
* 5、客户端、服务端通过get_key(size_t pub_key)方法获取密钥用于加密
* 6、客户端、服务端可使用crypto(char *data, size_t size, const char *key)方法加解密
class Crypto
public:
Crypto();
Crypto(size_t g, size_t p);
static void init();
size_t *get_public();
size_t get_pub_key();
char *get_key(size_t pub_key);
void crypto(char *data, size_t size, const char *key);
virtual ~Crypto();
protected:
size_t create_big_integer();
size_t pow_mod(size_t n, unsigned int times, size_t mod);
private:
size_t _g, _p;
size_t *_public;
size_t _private;
size_t _pub_key;
char *_pri_key;
#endif
#include "crypto.h"
#include <stdio.h>
#include <unistd.h>
#include <time.h>
Crypto::Crypto()
this->_g = (unsigned)rand()%9+2;
this->_p = create_big_integer();
this->_private = (size_t)rand()%this->_p;
this->_pub_key = pow_mod(this->_g, this->_private, this->_p);
this->_pri_key = new char[sizeof(size_t)+1];
this->_public = new size_t[2];
Crypto::Crypto(size_t g, size_t p)
this->_g = g;
this->_p = p;
this->_private = (size_t)rand()%this->_p;
this->_pub_key = pow_mod(this->_g, this->_private, this->_p);
this->_pri_key = new char[sizeof(size_t)+1];
this->_public = new size_t[2];
void Crypto::init()
srand((unsigned)time(0));
size_t *Crypto::get_public()
this->_public[0] = _g;
this->_public[1] = _p;
return this->_public;
size_t Crypto::get_pub_key()
return this->_pub_key;
char *Crypto::get_key(size_t pub_key)
size_t tmp = pow_mod(pub_key, this->_private, this->_p);
sprintf(this->_pri_key, "%08x", tmp);
return this->_pri_key;
void Crypto::crypto(char *data, size_t size, const char *key)
size_t len = strlen(key);
for(size_t i=0; i<size; ++i)
data[i] ^= key[i%len];
size_t Crypto::create_big_integer()
return ((size_t)((size_t)rand()<<16)|(size_t)rand());
size_t Crypto::pow_mod(size_t n, unsigned int times, size_t mod)
size_t tmp = 1;
for(unsigned int i=0; i<times; i++)
tmp = tmp*n%mod;
return tmp;
Crypto::~Crypto()
delete [] this->_public;
delete [] this->_pri_key;
#include <iostream>
#include <string.h>
#include "crypto.h"
using namespace std;
void print(char *data, int size)
for(int i=0; i<size; i++)
cout << data[i];
cout << endl;
int main(int argc, char** argv)
Crypto::init();
Crypto client;
size_t *g_p = client.get_public();
size_t X = client.get_pub_key();
Crypto server(g_p[0], g_p[1]);
size_t Y = server.get_pub_key();
char *K2 = server.get_key(X);
char *K1 = client.get_key(Y);
cout << "K1: " << K1 << "\nK2: " << K2 << endl << endl;
if(strcmp(K1, K2))
cout<< "会话密钥生成错误" << endl;
return 0;
char data[11] = "helloworld";
cout << "A加密: " << endl;
client.crypto(data, 10, K1);
print(data, 10);
cout << "==========" << endl;
cout << "B解密: " << endl;
server.crypto(data, 10, K2);
print(data, 10);
cout << "==========" << endl;
return 0;
原理中说的是生成随机大素数,在实现的时候我生成的是大整数,因为大素数生成是个麻烦的事情,我也尝试写过,但是生成速度太慢,影响体验。考虑到我们的加密方式是按位异或加解密,用这种方法就算不使用大素数依旧不会出问题,所以直接生成的是一个大整数,关于大素数的生成可以看一下 这篇文章,讲得挺好的。
d1 = pyDH . DiffieHellman ()
d2 = pyDH . DiffieHellman ()
d1_pubkey = d1 . gen_public_key ()
d2_pubkey = d2 . gen_public_key ()
d1_sharedkey = d1 . gen_shared_key ( d2_pubkey )
d2_sharedkey = d2 . gen_shared_key ( d1_pubkey )
d1_sharedkey == d2_sharedkey
默认情况下,它使用组 14(2048 位)。 使用另一个组(例如,15):
d1 = pyDH . DiffieHellman (
DH交换算法简介
Deffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一,它使得通信的双方能在非安全的信道中安全的交换密钥,用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法,之后被应用于安全领域,比如 Https 协议的 TLS(Transport Layer Security) 和 IPsec 协议的 IKE(Internet Key Exchange) 均以 DH 算法作为密钥交换算法。
DH算法
小明先选一个素数和一个底数,例如,素数p=23,底数g=5(底数可以任选),再选择一个秘密整数a=6,计算A=(g^a mod p)=8,然后大声告诉小红:p=23,g=5,A=8;
小红收到小明发来的p,g,A后,也选一个秘密整数b=15,然后计算B=(g^b mod p)=19,并大声告诉小明:B=19;
小明自己计算出s=(B^a mod p)
Diffie Hellman密钥协商用于在双方之间交换相同的秘密信息,例如交换对称加密的密钥,是基于离散对数困难问题的一个密钥协商协议。
所谓离散对数问题是说,有大素数p,
1、Diffie-Hellman算法简介
Diffie-Hellman算法(以下简称为:DH算法),是最早的密钥交换算法之一,它使得通信的双方能在非安全的信道中安全的交换密钥,用于加密后续的通信消息。
起基本流程原理如下:
假定小明和小红期望在一个不安全的网络中协商一个共同的密钥,那么进行如下步骤:
两人先说好大素数(质数)p和它的原始根g。
小明随机产生一个数a,并计算A = p^a mod g, 发送给小红。
小红随机产生一个数b,并计算......
Boblee人工智能硕士毕业,擅长及爱好python,基于python研究人工智能、群体智能、区块链等技术,并使用python开发前后端、爬虫等。1.Diffie-Hellman密钥协商算法Diffie-Hellman密钥协商算法在1976年在Whitfield Diffie和Martin Hellman两人合著的论文New Directions in Cryptography(Section Ⅲ...
如上原理,最后很容易通过数学原理证明(g^b%p)^a%p = (g^a%p)^b%p,因此它们得到一个相同的密钥。
上面除了a,b和最后得出的公共密钥是秘密的,其它都是可以在公共信道上传递。实际运用中p很大(300位以上),g通常取2或5。那么几乎不可能从p,g和g^a%p算出a(
diffie-Hellman(DH)算法原理
Diffie-Hellman算法是Whitefield Diffie和Martin Hellman在1976年公布的一种秘钥交换算法,它是一种建立秘钥的方法,而不是加密方法,所以秘钥必须和其他一种加密算法结合使用。这种秘钥交换技术的目的在于使两个用户安全的交换一个秘钥一遍后面的报文加密。
Diffie-Hellman密钥交换算法的有效性依赖于计算离散对数的难度。
1)由消息发送的一方构建密钥,这里由甲方构建密钥。
2)由构建密钥的一方向对方公布其公钥
DH密钥交换算法因为不能验证数据的来源,所以不能抵御中间人击.
如果需要安全强度更高的非对称加密算法,可以采用Ecc椭圆曲线加密算法或者使用广泛的RSA加密算法.
不对称加密算法主要用于在公共网络安全的数据传输.
不对称加密算法关键部分在于大整数数学函数库的使用.
C/C++实现的DH算法动态链接库,需要64位的可以自己手动编译.
Diffie-Hellman算法是第一个公开密钥算法,早在 1976 年就发现了。其安全性源于在有限域上计算离散对数,比计算指数更为困难。该算法可以使两个用户之间安全地交换一个密钥,但不能用于加密或解密信息。
该算法是一种建立密钥的方法,并非加密方法,但其产生的密钥可用于加密、密钥管理或任何其它的加密方式,这种密钥交换技术的目的在于使两个用户间能安全地交换密钥(KEY)以便用于今后的报文加密。该算法需要公开两个参数:质数 n 和其原根 g,同时通信双方 A 和 B 随机选择自己的私钥 x 和 y,通过交换g
(1) 选择公共数p,a;
(2) 用户Alice选择一个秘密数Xa,并将自己的公钥Ya = (a^Xa) mod p发送给用户Bob
(3) 用户Bob选择一个秘密数Xb,并将自己的公钥Yb = (a^Xb)mod p发送给用户Alice
(4) Alice计算 共享密钥Ka = (Yb^Xa) mod p
(5) Bob计算 共享密钥Kb =(Ya^Xb) mod p
(6) 此时 Ka =Kb
程序实现
#include<iostream&

