【斯坦福CS224W图与机器学习11】Link Analysis: PageRank
本节主要介绍了PageRank以及其在二部图推荐中的应用【 ppt传送 】【 视频传送 】,主要包括了三个方面:
- Web as a Graph
- PageRank
- Random Walk with Restarts and Personalized PageRank
Web as a Graph
PageRank算法最初是Google用于网页排序的算法,首先介绍一下网页的图结构以及一些概念。网页可以看作一个图,其中节点是网页,边是网页之间的连接。下图为一个网页的有向图,每个蓝色部分都链接到下一个链接。
几种类型的有向图:
- 强连接:有向图中任意两个节点之间都能互相到达,如图所示
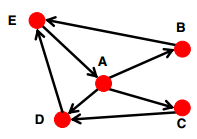
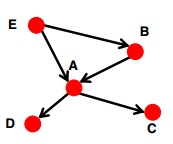
- 有向无环图:没有环,即如果节点u可以到达节点v,那么节点v不能到达节点u,如图所示
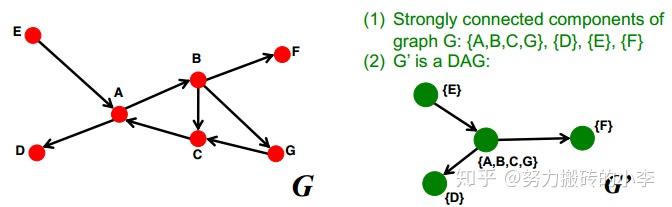
- 强连通分量(Strongly Connected Component):图中一个子图包含一系列节点S,S中每个节点都可以互达,并且没有更大的集合可以可以满足这个性质了,如下图所示,有4个强连通分量:{A,B,C,G}, {D}, {E}, {F}
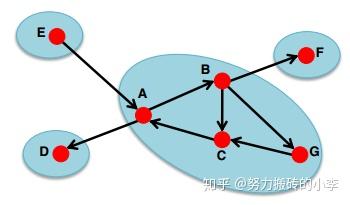
- 结论:任何一个有向图都是它强连通分量上的有向无环图
证明:
1)把每个强连通分量看作是图G的节点,也就是说,每个强连通分量代表一个节点,如下图所示,图G有4个连通分量,对应图G'中4个节点
2)构建图G',节点为强连通分量,如果在原图中,两个强连通分量之间有边相连,则在新图G'中,这两个对应的节点也有边相连,如下图所示,可以看出,图G'为有向无环图。
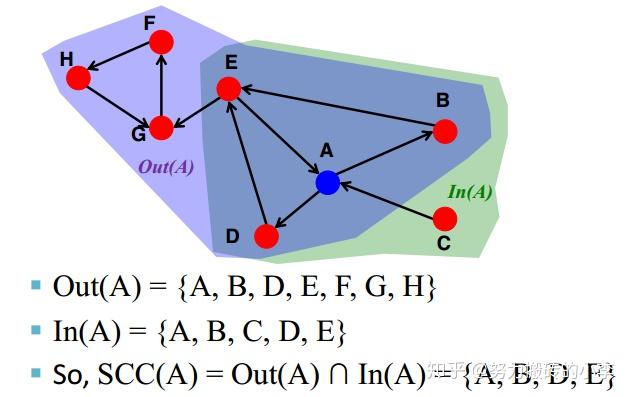
- 怎样找到包括节点v的强连通分量?
SCC=Out(A) \cap In(A) ,即通过节点能到达的集合,和能到达节点的集合取交集,即为包含该节点的强连通分量,如下图所示,包含节点A的强连通分量为{A,B,D,E}
PageRank
PageRank最初是用于计算网页重要性的一种迭代算法,它认为:
- 网页如果经常被其他网页连接,那么它很重要;
- 如果网页被一个很重要的网页连接,这个网页也会因为这个连接的重要网页而变得重要。
定义节点 r_j 的“rank”: r_j=\sum_{i\rightarrow j}\frac{r_i}{d_i} ,其中 d_i 为节点i的出度。即每个节点的rank由指向它的节点的出度来决定。如下图所示。
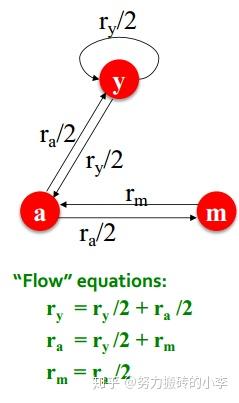
可以利用矩阵形式来表达上式,即 r=Mr ,M是随即邻接矩阵,如果 j\rightarrow i ,则 M_{ij}=\frac{1}{d_j} ,比如在上图中, M=\begin{pmatrix}\frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 1 \\ 0 &\frac{1}{2} & 0 \end{pmatrix} ,即 \begin{pmatrix}r_y \\ r_a \\r_m \end{pmatrix}=\begin{pmatrix}\frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 1 \\ 0 &\frac{1}{2} & 0 \end{pmatrix} = \begin{pmatrix}r_y \\ r_a \\r_m \end{pmatrix}
那么就可以通过上式不断迭代,直至收敛,简单的算法原理为:
- Step1:初始化 r^{(0)}=[\frac{1}{N},...,\frac{1}{N}]^T
- Step2:迭代 r^{(t+1)}=Mr^{(t)}
- Step3:重复第二步直至 |r^{(t+1)}-r^{(t)}|<\epsilon
比如说,对于上图例子中,先初始化 \begin{pmatrix}r_y \\ r_a \\r_m \end{pmatrix}=\begin{pmatrix}\frac{1}{3} \\ \frac{1}{3} \\\frac{1}{3} \end{pmatrix} ;
然后利用 r=Mr 不断迭代:

最终稳定时三个节点的rank(重要性)为: \begin{pmatrix}r_y \\ r_a \\r_m \end{pmatrix}=\begin{pmatrix}\frac{6}{15} \\ \frac{6}{15} \\\frac{3}{15} \end{pmatrix}
但是上述算法一定收敛吗?一定会收敛到我们想要的结果吗?结果是合理的吗?
上述算法有两个问题:
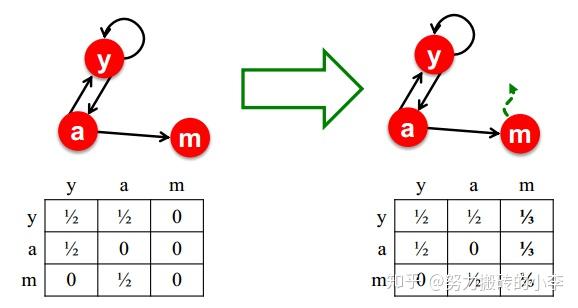
- 问题一:dead ends,就是说有些节点没有out-links(出边),如下图所示,初始为 \begin{pmatrix}r_a \\ r_b \end{pmatrix}=\begin{pmatrix}\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} ,由于b没有出边,不断迭代后, \begin{pmatrix}r_a \\ r_b \end{pmatrix}=\begin{matrix}\frac{1}{2} &0&0&0&0 \\ \frac{1}{2} &\frac{1}{2}&0&0&0 \end{matrix} ,所有节点的重要性均为0,并不是我们想要的收敛结果

为了解决问题一,可以调整M矩阵,在dead ends时,以相同的概率跳转到其他节点,如下图所示:
- 问题二:Spider traps,所有节点都指向一个节点,最终节点所有重要性都会被一个节点吸收,如下图所示,初始为 \begin{pmatrix}r_a \\ r_b \end{pmatrix}=\begin{pmatrix}\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} ,由于所有节点都指向b,不断迭代后, \begin{pmatrix}r_a \\ r_b \end{pmatrix}=\begin{matrix}\frac{1}{2} &0&0&0&0 \\ \frac{1}{2} &1&1&1&1 \end{matrix} ,会发现节点b的重要性为1,而节点a没有重要性,这显然是不合理的。
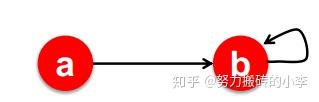
为了解决问题二,在每一步时:
- 以概率 \beta 正常游走
- 以概率 1-\beta 随机跳到一个网页(节点)上
\beta 通常介于0.8-0.9之间,这样游走序列就不会陷入某个局部节点了
通过上述分析, PageRank表达式为:
r_j=\sum_{i\rightarrow j}\beta \frac{r_i}{d_i}+(1-\beta)\frac{1}{N}
矩阵形式为: r=\beta M\cdot r+[\frac{1-\beta}{N}]_N ,其中 [(1-\beta)/N]_N 为所有元素均为 (1-\beta)/N 的N维矩阵
下图为一个迭代例子( \beta=0.8 ):
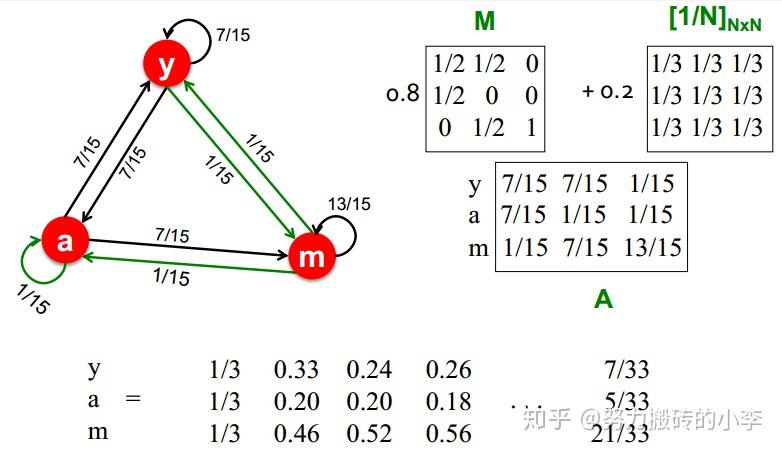
M是一个稀疏矩阵,而 [\frac{1-\beta}{N}]_N 为一个稠密矩阵,因此,为了减轻计算复杂度,我们在每一轮迭代中,计算 r^{new}=\beta M\cdot r^{old} ,然后在 r^{new} 的基础上,添加一个常数值 (1-\beta)/N ,流程如图所示:

Random Walk with Restarts and Personalized PageRank
下面介绍了PageRank在推荐中的应用。
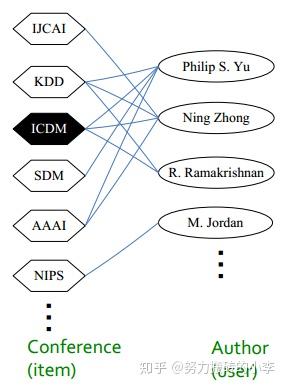
现在有一个Conference-to-authors二部图,如图所示,我们想知道和ICDM最相关的会议是哪个?我们应该为M.Jordan推荐哪个会议参加?这种给定一个节点,判断其他节点对其的”重要程度“正是PageRank算法的思想。推荐问题就是,给定一个节点,来计算其他节点对于它的重要程度(PageRank)并排序,根据PageRank大小排序后进行推荐。
方法:给定一个query-nodes集合,模拟随机游走
- Step1:随机访问邻居节点,并且记录访问次数
- Step2:以概率 \alpha 重新在query-nodes上游走(回到某初始点)
- Step3:访问次数最多的节点和query-nodes最接近,是要被推荐的对象
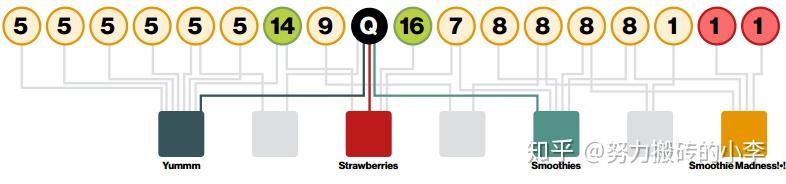
下图为一个例子,其中数字表示访问自处,对于节点Q来说,访问次数16的节点为与其相似度最高的节点。这种方法考虑了多重连接、多重路径,直接连接和间接连接,以及节点度数。
- Normal Pagerank:每个节点被访问的次数相同
- Personalized Pagerank:节点可以根据不同的权重被访问的概率不同
- Random Walk with Restarts:可以以一定的概率方会到初始节点
系列文章:
【斯坦福CS224W 图与机器学习(1-2)】:图模型基本介绍
【斯坦福CS224W 图与机器学习 3】:Motifs and Structural Roles
【斯坦福CS224W 图与机器学习 4】Community Structure in Network
【斯坦福CS224W 图与机器学习 5】Spectral Clustering
【斯坦福CS224W 图与机器学习6】Message Passing&Classification
