;
但是这样又一个坏处 因为d是从1开始一直自增1去遍历 所以n1不能太大 也就是说p和q不能太大 但是本身p,q需要是大质数 这样才能保证加密的性能
需要用到扩展欧几里得算法求乘法逆元d
要了解扩展欧几里得算法我们需要先知道贝祖定理:
若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.
所以 通常谈到最大公约数时,我们都会提到一个非常基本的事实:给予二个整数a、b,必存在整数x、y使得ax + by = gcd(a,b)。
有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数——这是众所周知的。然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
扩展欧几里得算法可以用来计算模反元素(也叫模逆元),而模反元素在RSA加密算法中有举足轻重的地位。
我们举个例子:
用类似辗转相除法,求二元一次不定方程47x+30y=1的整数解
这个过程也可以用矩阵表示 q表示商,r表示余数
那么使用扩展欧几里德算法的过程应该是这样:
求exgcd(e, m)—>利用欧几里得算法不断递归直到x=1,y=0—>反向递归求出第一层的x和y,x即为e模m的逆元。
用代数表示一下 就是
我们要处理的是求出 a 和 b的最大公约数,并求出 x 和 y 使得 a*x + b*y= gcd ,而我们已经求出了下一个状态:b 和 a%b 的最大公约数,并且求出了一组x1 和y1 使得: b*x1 + (a%b)*y1 = gcd , 这两个相邻的状态之间应该存在一种关系
那么我们来验证一下:
我们给出这一条定理: a%b = a - (a/b)*b //c系语言的除是取整数部分的除 因为欧拉定理我们清楚地知道 gcd(a,b)= gcd(b,a % b)
gcd = b*x1 + (a-(a/b)*b)*y1
= b*x1 + a*y1 – (a/b)*b*y1
= a*y1 + b*(x1 – a/b*y1)
对比之前我们的状态:求一组 x 和 y 使得:a*x + b*y = gcd
根据恒等定理 系数是不是要相同啊:
x = y1
y = x1 – a/b*y1
这时候 我们就可以写出扩展欧几里得算法
int exgcd(int a2,int b2,int &x,int &y)
if(b2==0)
x=1;y=0;
return a2;
int ans = exgcd(b2,a2%b2,x,y);
double temp=x;
x=y;
y=temp-a2/b2*y;
return ans; ///返回的还是最大公约数 但是我们就方便求x和y
这时候 我们很方便地可以求x和y 也就可以求出乘法逆元
乘法逆元是: ed mod φ(N)=1
也就存在这个表达式 ed +kφ(N)= 1 根据前边我们知道当gcd(ed φ(N)) != 1 的时候是没有解
一般,根据不定方程等数论部分的知识 我们应该能够找到无数组解满足条件,但是谁会闲的无聊让你写一堆通解
一般是让你求解出最小的那组解,怎么做?我们求解出来了一个特殊的解 x0 那么,我们用 x0 % φ(N)其实就得到了最小的解了
因为啊 d的通解正是x0+kt
也就是说 d对于 φ(N) 的逆元是一个关于 φ(N) 同余的
那么根据最小整数原理,一定存在一个最小的正整数,它是 d 关于φ(N) 的逆元,而最小的肯定是在(0 , φ(N))之间的,而且只有一个 这些都是纯数学推导
不得不说数学真的很重要
这时候还有一点要注意 我们有时候得到的x0可能是负数 所以要用函数abs()取绝对值
至此 所有RSA加密的问题都迎刃而解了
现在我给出模拟RSA加密的总代码
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b)///辗转相除法求最大公约数
int t = a;
while(a%b!=0)
a=b;
b=t%b;
t=a;
return b;
int x,y,q;
int exgcd(int a2,int b2,int &x,int &y)
if(b2==0)
x=1;y=0;
return a2;
int ans = exgcd(b2,a2%b2,x,y);
double temp=x;
x=y;
y=temp-a2/b2*y;
return ans; ///返回的还是最大公约数 但是我们就方便求x和y
int tocal(int a3,int b3)
int x0,y0;
int gcd = exgcd(a3,b3,x0,y0);
if(1%gcd!=0) return -1; ///gcd得等于1 ...
x0*=1/gcd;
b3=abs(b3);
int ans = x0%b3;
if (ans<=0) ans+=b3;
return ans;
int main()
int p, q;
cout << "输入p、q (p、q为质数)" << endl;
cin >> p >> q;
int n = p * q;
int n1 = (p - 1) * (q - 1);///欧几里得函数
int e;
cout << "输入e (e是与" << n1 << "互质的) 且 1<e<" << n1 << endl;///按照定义来
cin >> e;
int d;
/*其实也可以穷举法求d 但是这样 输入的p和q不能过大 所以n1才不会太大
for (d = 1;; d++) ///求d d是e的乘法逆元
if (d * e % n1 == 1)
break;
d = tocal(e,n1);
cout << endl << endl;
cout << "{ " << e << "," << n << " }" << "为公钥" << endl;
cout << "{ " << d << "," << n << " }" << "为私钥" << endl;
cout << endl << endl;
int before;
cout << "输入明文,且明文小于"<<n << endl;
cin >> before;
cout << endl;
int i;
cout << "密文为" << endl;
int after;
after = before % n;
for (i = 1; i < e; i++)
after = (after * before) % n;
cout << after << endl;
cout << "明文为" << endl;
int real;
real = after % n;
for (i = 1; i < d; i++)
real = (real * after) % n;
cout << real << endl;
return 0;
运行结果:完全正确
后来地球上出现了迄今为止最重要的非对称加密RSA算法。
公钥对外公开 而私钥自己保有
世界上很多事情,都是单向(或者反向问题难度大大增加)的。杀一个人比救一个人容易 摔碎一个餐具比拼好一个餐具容易 研究毒药比研究毒药的解药容易
令两个大素数相乘容易 把一个大数分解成两个素数相乘就很难
解密确实用了私钥,一个跟加密过程不一致的方式。即解密并不是我们常识理解的那种逆运算,比如1+1=2,反过来2-1=1。但是RSA却不是这样很显然的方式
所以才叫非对称加密 这样对概念也就能深深的理解
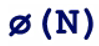 是N的欧拉函数
是N的欧拉函数