多元多次函数自动求导在梯度下降中的应用

Feifei

想做科研的工程师

代码地址： https://github.com/13372034568/machine_learn/ 下面的“工具类.py”

本文所说的自动求导，还停留在多项式求导上；

因为最终需要用图像进行展示，所以，选择了二元二次多项式作为示例。

因为为多项式，所以定义元组用于存储每一元的系数、指数，每一元本身也是多项式。元组的输出如下：

[[(1, 2), (-3, 1)], [(46, 2), (-39, 1), (-27, 0)]]

可以表示为：z = X^2 - 3 * X + 46 * Y^2 - 39 * y - 27

空间曲面如下所示：

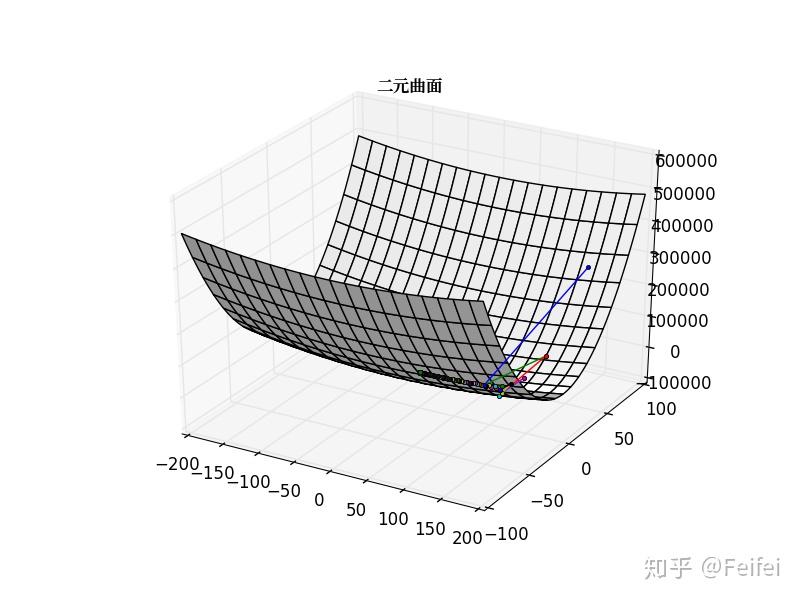
里面的彩色线为梯度下降逼近轨迹

等高线形式表示如下：

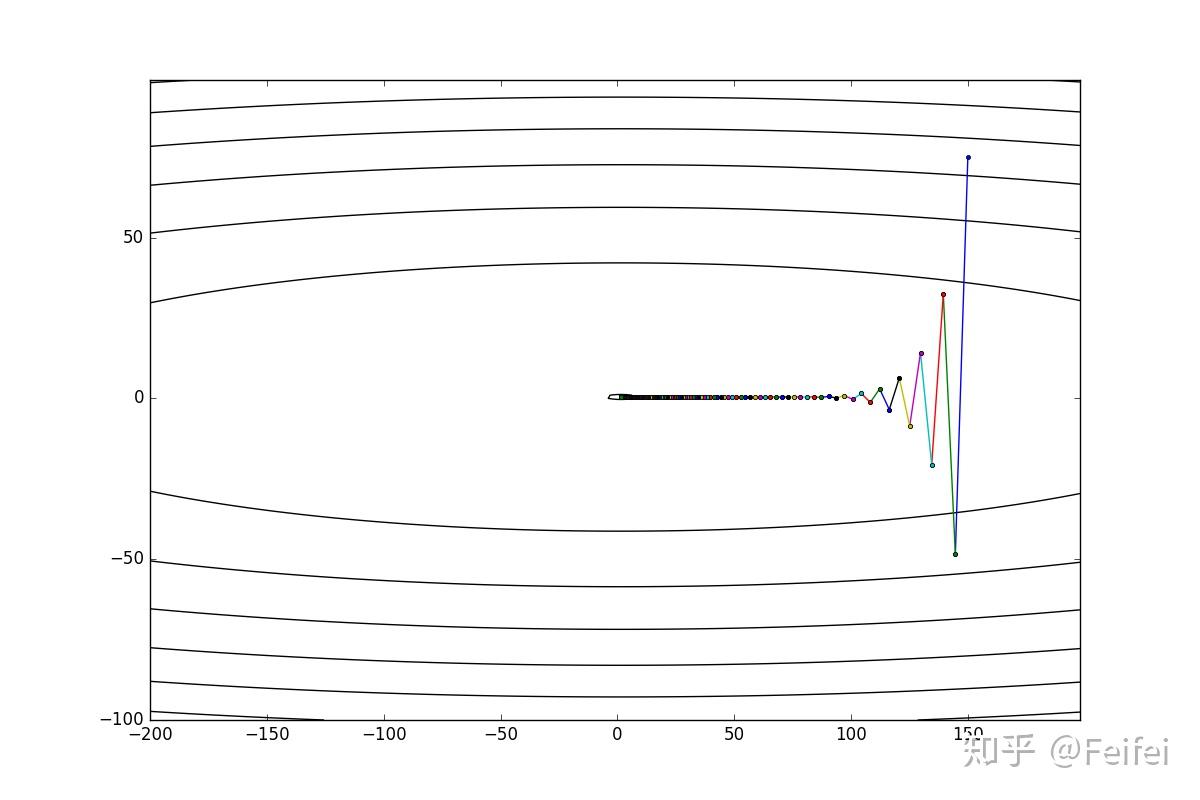
代码包含几个独立模块，分别负责

（1）构造一个多元多次函数所需要的各元系数、指数

def 创建多元多次函数(元数, 最大次数, 系数范围):
    元组 = []
    for 元项序号 in range(元数):
        元项 = []
        次数列 = list(range(0, 最大次数 + 1))
        采样数 = randint(1, 最大次数 + 1)
        次数采样 = sample(次数列, 采样数)
        次数采样.sort(reverse=True)
        当前系数范围 = 系数范围[元项序号]
        for e, 次数 in enumerate(次数采样):
            if e == 0:
                系数 = randint(1, 当前系数范围[1])
            else:
                系数 = randint(当前系数范围[0], 当前系数范围[1])
            元项.append((系数, 次数))
        元组.append(元项)
    return 元组

（2）实例化多元多次函数

def 实例化多元多次函数(元组, 自变量取值范围, 步长, 使用笛卡尔=False):
    if 使用笛卡尔:
        自变量集 = 生成自变量笛卡尔集(自变量取值范围, 步长)
    else:
        自变量集 = 生成自变量同步集(自变量取值范围, 步长)
    自变量取值 = [[] for _ in 元组]
    应变量取值 = []
    for 自变量 in 自变量集:
        应变量 = 计算多元多次函数(元组, 自变量)
        应变量取值.append(应变量)
        for 自变量序号, 自变量单维度取值 in enumerate(自变量):
            自变量取值[自变量序号].append(自变量单维度取值)
    return 自变量取值, 应变量取值

（3）通过自变量求解应变量

def 计算多元多次函数(元组, 自变量列表):
    assert len(元组) == len(自变量列表)
    应变量计算值 = 0
    for 元组序号, 元项 in enumerate(元组):
        元项计算值 = 0
        自变量值 = 自变量列表[元组序号]
        for 系数, 次数 in 元项:
            元项计算值 += 系数 * np.power(自变量值, 次数)
        应变量计算值 += 元项计算值
    return 应变量计算值

（4）对多元多次函数的求导过程

def 求导数(元组, 自变量列表):
    assert len(元组) == len(自变量列表)
    导数向量 = []
    for 元组序号, 元项 in enumerate(元组):
        元项导数值 = 0
        自变量值 = 自变量列表[元组序号]
        for 系数, 次数 in 元项:
            if 次数 == 0:
                元项导数值 += 0
            else:
                元项导数值 += 次数 * 系数 * pow(自变量值, 次数 - 1)
        导数向量.append(元项导数值)
    return np.array(导数向量)

（5）梯度下降

def 梯度下降(元组, 自变量起始列表, 学习率, 梯度停止阈值, 最大迭代数, 求导函数):
    x = np.array(自变量起始列表, dtype='float64')
    passing_dot = [x.copy()]
    for i in range(最大迭代数):
        grad = 求导函数(元组, x)
        x -= grad * 学习率
        passing_dot.append(x.copy())
        print('[ Epoch {0} ] grad = {1}, x = {2}'.format(i, grad, x))
        if abs(sum(grad)) < 梯度停止阈值:
            break
    return x, passing_dot

（6）使用matplotlib绘制空间函数曲线、等高线

def 绘制多元多次函数曲线(元组, 自变量取值, 应变量取值, 模式="曲线", 梯度下降轨迹=None, fp=None):
    plt.grid(True)
    if len(自变量取值) == 2:
        x = 自变量取值[0]
        y = 自变量取值[1]
        X, Y = np.meshgrid(x, y)
        Z = 计算多元多次函数(元组, [X, Y])
        if 模式 == "等高线":
            plt.figure(figsize=(12, 8))
            plt.contour(X, Y, Z, colors='black')
            if 梯度下降轨迹 is not None:
                arr = np.array(梯度下降轨迹)
                for i in range(len(arr) - 1):
                    plt.plot(arr[i:i + 2, 0], arr[i:i + 2, 1], marker="o", markersize=3)
        elif 模式 == "曲面":
            fig = plt.figure()
            ax = fig.gca(projection='3d')
            ax.set_title("二元曲面", fontproperties=chs_font)
            # ax.plot_surface(X, Y, Z, cmap='rainbow')
            ax.plot_surface(X, Y, Z, color='white')
            if 梯度下降轨迹 is not None:
                arr = np.array(梯度下降轨迹)
                for i in range(len(arr) - 1):
                    plt.plot(arr[i:i + 2, 0], arr[i:i + 2, 1], arr[i:i + 2, 2], marker="o", markersize=3)
                ax.legend()
        elif 模式 == "曲线":
            fig = plt.figure()
            ax = fig.gca(projection='3d')
            ax.set_title("二元多次曲线", fontproperties=chs_font)
            ax.plot(x, y, 应变量取值,
                    color='r', linewidth=1, label="2d curve")
            ax.legend()
        else:
            plt.close()
            return
    elif len(自变量取值) == 1:
        x = 自变量取值[0]
        plt.plot(x, 应变量取值, linewidth=1)
    else: