计算两点之间的方位角

geoday

首先说明下对于方位角的界定，是正北方向顺时针0-360度。

平面

首先：根据math.atan2求出原点至点(dx,dy)的方位角，即与 x 轴的夹角，单位为弧度，取值范围为（-π，π】。

然后：将上述方位角进行转换成正北方向（y轴）顺时针的方位角。

import math
# 计算两点之间的方位角
# 输入两个点的坐标，输出方位角，单位为度
def bearing(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    return (90 - math.degrees(math.atan2(dy, dx)) + 360) % 360
print(bearing(0, 0, 100, -100))  # 135.0

球面

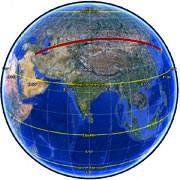
通常沿着大圆路径（great circle path），两点之间的方位角并不是恒定的，与两点之间的距离和纬度相关。如下图所示从巴格达到大阪，起点的方位角约为60度，终点的方位角约为120度。

针对起点的方位角，其计算公式如下，

θ = \arctan2*(\sin Δα* \cos β2 , \cos β1*\sin β2-\sin β1*\cos β2* \cos Δα )

其中α1,β1 为起点坐标（单位为弧度）, α1,β1为终点坐标（单位为弧度），Δα为经度的差值。

import math
# 计算两点之间的方位角
# 输入两个点的经纬度坐标，输出球面上起点方位角，单位为度
def bearing(lon1, lat1, lon2, lat2):
    β1 = math.radians(lat1)
    β2 = math.radians(lat2)
    dα = math.radians(lon2) - math.radians(lon1)
    y = math.sin(dα) * math.cos(β2)
    x = math.cos(β1) * math.sin(β2) - math.sin(β1) * math.cos(β2) * math.cos(dα)
    brng= (math.degrees(math.atan2(y, x)) + 360) % 360
    return brng
print(bearing(45, 35, 135, 35))  # 60.16243352168624 起点为伊拉克的巴格达，终点为日本的大阪

针对终点的方位角，在原来的基础上先将起点和终点互换，然后再进行如下转换

θ = (θ+180)\%360

import math
# 计算两点之间的方位角
# 输入两个点的经纬度坐标，输出球面上起点方位角，单位为度
def bearing(lon1, lat1, lon2, lat2):
    β1 = math.radians(lat1)
    β2 = math.radians(lat2)
    dα = math.radians(lon1) - math.radians(lon2)
    y = math.sin(dα) * math.cos(β1)
    x = math.cos(β2) * math.sin(β1) - math.sin(β2) * math.cos(β1) * math.cos(dα)