Python环境下应用Cplex求解最优化问题

4 天前

躺平生活

怎么样

1.python环境

注意，本文默认已经会使用pycharm和python的语法。使用Python3.10和Cplex12.10版本。本文使用的cplex是pip直接下载的免费版本，在求解上有限制，想要安装不受限制的版本可以看： https:// zhuanlan.zhihu.com/p/65 5434273

1.1导入cplex包

可以使用命令框执行，需要网络环境较好的情况下执行，大概下载30M不到的文件。

pip install cplex

或者如下在pycharm内settings下的python interpreter内点加号搜索cplex下载。

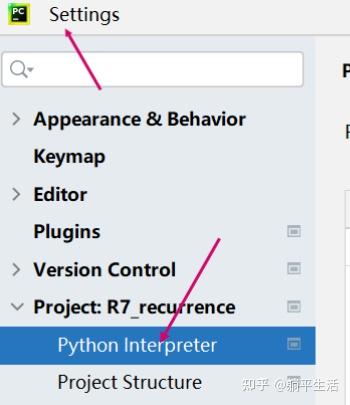
下载好后，使用时只需要添加如下语句导入cplex的包

import cplex

1.2创建cplex对象

使用如下代码进行cplex对象的创建。注意：后面使用的语句都是当前创建的cplex_obj。

cplex_obj = cplex.Cplex()

当然，在创建时也可以选择初始化一些参数，如下

cplex_obj = cplex.Cplex(param={'timelimit': 10, 'mipgap': 0.1})

这句代码的意思是设置了第一个参数时间限制10秒，即，在10秒内要给出求解的最优值；第二个参数设置最优性间隙10%，即，当现在求解的最优值与真实最优值的差距不超过10%。

1.3添加变量

使用如下语句进行变量的添加

x = cplex_obj.variables.add(names=['x'],lb=[0],ub=[1],types=['I'],obj=[1],init=[0])

在上面语句中，names是设置变量名称；lb设置变量下界；ub设置变量上界；types设置变量的类型，'C'连续值类型，'I'整数值类型，'B'二进制类型；obj设置目标函数系数，init设置初始值。所以上面的语句意思：x的整数变量，下界为0，上界为1，目标函数系数为1，初始值为0。

1.4设置目标函数

使用如下的语句设置线性目标函数

cplex_obj.objective.set_linear(“目标函数”)

“目标函数”：是一个字典，表示目标函数的系数。字典的键是变量名，值是对应的系数。对于如何应用，下面举一个小例子

x = cplex_obj.variables.add(name=['x'], types=['C'],lb=[0],ub=[1])
y = cplex_obj.variables.add(names=['y'], types=['C'],lb=[0],ub=[1])
cplex_obj.objective.set_linear([(x, 1), (y, 2)])
cplex_obj.objective.set_sense(cplex_obj.objective.sense.maximize)

这是设置了x，y的两个连续值变量，然后设置了目标函数 x+2y ，并求解最大值（第四句设置优化方向为最大值）。注意，即使是单个变量的添加，也需要使用括号"[ ]"，不然会报错，TypeError: object of type 'int' has no len()或者TypeError: object of type 'float' has no len()等；这里添加求解函数的时候，可以使用1.5中添加约束所用的方式，即，[['x', 'y'], [1.0, 1.0]]，完整语句如下所示。

cplex_obj.objective.set_linear([['x', 'y'], [1.0, 1.0]])

1.5添加约束

添加约束使用如下表达式

cplex.linear_constraints.add(lin_expr, senses, rhs, range)

该方法有两个必选参数：（1）lin_expr表示线性表达式列表，每个线性表达式是一个系数-变量元组的列表，表示约束左侧的线性表达式；（2）sense表示约束类型，参数是一个字符串列表，表示每个约束的类型，可以是L（小于等于）、E（等于）或G（大于等于）。

该方法还有三可选参数：（1）rhs表示右侧常数；（2）range，如果不为None，则表示约束类型为R（范围约束），同时需要指定range参数为一个表示范围的浮点数；（3）names设置约束的名称。

为了方便理解，下面举一个例子

cplex_obj.linear_constraints.add(lin_expr=[[['x', 'y'], [1.0, 2.0]]], senses=['L'], rhs=[30], names=['st1'])
cplex_obj.linear_constraints.add(lin_expr=[[['x', 'y'], [1.0, 1.0]]], senses=['L'], rhs=[15], names=['st1'])

为目标函数 x+2y 添加了两个约束，分别是：（1） x+2y\leq 30 ；（2） x+y \leq 15 。注意，在使用时发现不能使用与添加目标函数时一样的格式：[('x',1.0),('y',2.0)]，如下语句会报错。

cplex_obj.linear_constraints.add(lin_expr=[[('x',1.0),('y',2.0)]],senses=['L'],rhs=[30],names=['st1'])

要使用如下的格式才能正确求解，并且要注意这里有三层括号，因为原本表达式就是两层括号，而这里再加了一层括号。再加一层括号的理由与1.4例子里添加单个变量的理由一样，即，不加会报错。

cplex_obj.linear_constraints.add(lin_expr=[[['x','y'],[1.0,2.0]]],senses=['L'],rhs=[30],names=['st1'])

1.6求解模型

求解模型使用如下语句

cplex_obj.solve()

该语句它会自动调用设置好的求解算法来求解模型。在CPLEX中，求解模型的过程分为两个阶段：预处理和求解（本文不详细展开讲）。

1.7获取结果

获取结果使用如下语句

solution = cplex_obj.solution.get_values()

如上语句，变量的求解值已经赋值给solution，可能是一个变量，也可能是多个变量，可以通过下面语句，获取具体名称的求解变量值（名称为x的变量值）

x_result = cplex_obj.solution.get_values('x')

注意，在获取求解结果的时候，要保证求解成功，否则会出现问题。可以使用如下语句对进行检查

if cplex_obj.solution.is_primal_feasible():
    print("Solution is feasible")
    # 获取解
    solution = cplex_obj.solution.get_values()
    print(solution)
else:
    print("Solution is infeasible")

检查是可行解后，再获取求解值并输出。

1.8设置值和获取值

1.8.1设置值

在上面所介绍的添加变量、目标函数和添加约束中，可以直接在语句中对参数进行初始化，也可以使用下面的方式，设置语句的参数

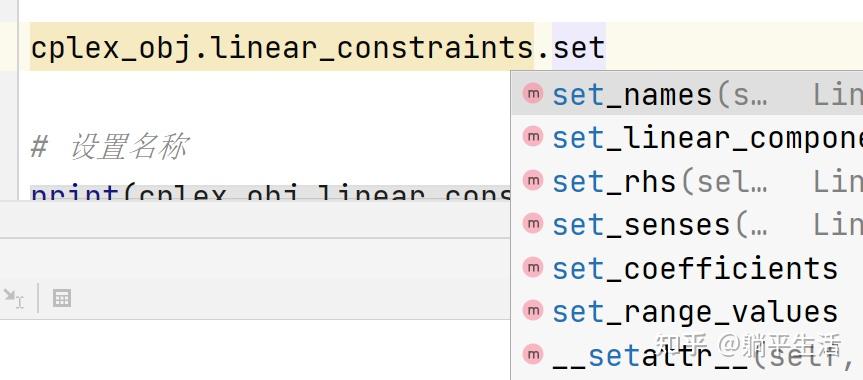
cplex_obj.linear_constraints.set_names(1,'st3')

使用set_names对约束条件的名称进行设置，1表示列表第二个约束（从0开始计数），'st3'表示设置的约束名称。注意，这里只是列举了设置约束名称的方法，同样其他的语句，其他的参数都可以使用类似的语句设置，如下所示

cplex_obj."对应的语句".set_"对应参数"

对应的图，图中均为可以设置的部分

1.8.2获取值

同样，可以如1.8.1设置值，也可以类似的获取值

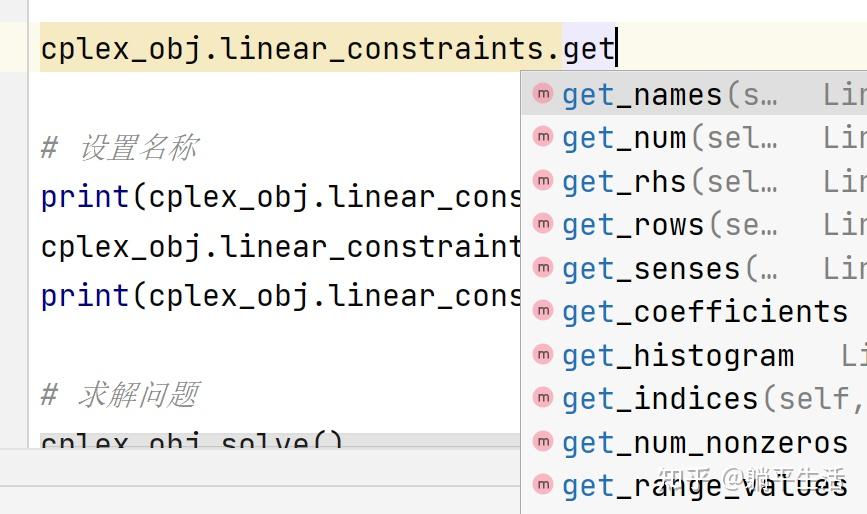
name = cplex_obj.linear_constraints.get_names(1)

获取列表第二个约束的名称（列表从0开始），返回给name变量。注意，与1.8.1类似，其他的语句，其他的参数都可以使用类似的语句获取，如下所示

cplex_obj."对应的语句".get_"对应参数"

对应的图，图中均为可以获取的部分，具体的参数作用不再展开讨论。

1.9测试使用的代码

这是一个临时使用测试的代码，一个简单的线性规划表达式如下

argmax:x+2y

st.x+2y \leq 30

x+y\leq 15

x\in [0,10]

y\in [0,10]

import cplex as cp
# 创建cplex对象
cplex_obj = cp.Cplex()
# 创建连续值变量
x = cplex_obj.variables.add(names=['x'], types=['C'], lb=[0], ub=[10])
y = cplex_obj.variables.add(names=['y'], types=['C'], lb=[0], ub=[10])
# 创建目标函数（线性）
cplex_obj.objective.set_linear([('x', 1.0), ('y', 2.0)])
# 设置优化方向（最大化）
cplex_obj.objective.set_sense(cplex_obj.objective.sense.maximize)
# 添加约束
cplex_obj.linear_constraints.add(lin_expr=[[['x', 'y'], [1.0, 2.0]]], senses=['L'], rhs=[30], names=['st1'])
cplex_obj.linear_constraints.add(lin_expr=[[['x', 'y'], [1.0, 1.0]]], senses=['L'], rhs=[15], names=['st2'])
# 设置名称，测试set_names和get_names
print(cplex_obj.linear_constraints.get_names(1))
cplex_obj.linear_constraints.set_names(1,'st3')
print(cplex_obj.linear_constraints.get_names(1))
# 求解问题
cplex_obj.solve()
# 检查求解可行性
if cplex_obj.solution.is_primal_feasible():