DID会固定年份吗_双重差分方法(DID)解析、影响机制分析与三重差分方法(DDD)...
Copyright @计量经济圈 & 经管一只小蚂蚁整理转载
只用于学习与交流,为其提供一些参考依据。
一、双重差分解析
双重差分方法近几年在主流期刊流行起来(这种趋势大概会持续几年),主要原因在于:(1)
可以很大程度上避免内生性问题
,政策相对于微观经济主体而言一般是外生的,因而不存在逆向因果问题。此外,使用固定效应估计一定程度上也能缓解遗漏变量偏误问题。(2)传统方法下评估政策效应,主要是通过设置一个政策发生与否的虚拟变量然后进行回归,相较而言,
双重差分法的模型设置更加科学
,能更加准确地估计出政策效应。(3)
双重差分法的原理和模型设置很简单
,容易理解和运用,并不像空间计量等方法一样让人望而生畏。(4)尽管
双重差分法估计的本质就是面板数据固定效应估计
,但是DID听上去或多或少也要比OLS、FE之流更加“时尚高端”,因而DID的使用一定程度上可以满足“虚荣心”。
DID
只适用于面板数据
,当然特殊的截面数据只要能构造出双重差分项就可以运用DID。大神Duflo曾经就使用截面数据和DID研究了南非的养老金计划项目对学前儿童健康的影响。
基准DID模型设定如下:

其中,du为分组虚拟变量,若个体i收到政策影响,则个体i属于处理组(实验组),对应的du取值为1,若个体不受到政策的影响,则个体i属于对照组。dt为政策实施的时间虚拟变量,政策实施之前为0,之后取1。du×dt为上述两个虚拟变量的交互项,也就是构造的双重差分项,其估计系数
α
3为政策实施的净效应。
注意:
从DID的模型设置来看,要想使用DID必须满足以下两个关键条件:一是必须存在一个具有试点性质的政策冲击,这样才能找到处理组和对照组,那种一次性全铺开的政策并不适用于DID分析;二是必须具有一个相应的至少两年(政策实施前后各一年)的面板数据集。
为什么交互项(双重差分项)的系数
α
3就能体现政策的净效应?双重差分项真正内涵如下表所示。

很多文献中采用数学表达式,如下所示,

以上阐述了双重差分方法的基本原理,其核心思想就是通过对政策前后对照组与处理组之间的差异的比较,进而构造出反映政策效果的双重差分统计量。将该思想转化为简单的模型(1),这个时候只需要关注模型的交互项系数
α
3就可以得到政策效应。
更进一步地,可以由下图形象反映出DID的基本思想。
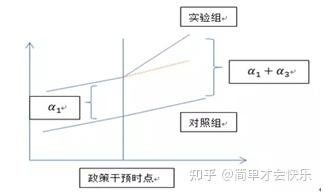
上图也反映出DID方法的一个重要的基本假设——共同趋势假设,即处理组与控制组在政策实施之前必须具有相同的发展趋势。DID的使用不需要政策随机与分组随机,只需要满足共同趋势假设。怎么检验?参考上一篇推文。
很多时候,在很多比较高大上的文献中,经常设置与模型(1)不太一样的模型,可以设定如下:

该模型只有交互项du×dt,而缺少处理组与控制组的虚拟变量以及时间虚拟变量,其实模型(2)与模型(1)的本质是一样的,模型(2)更常见于有多年面板数据类型。其中,
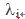
为个体效应,更能反映个体特征,代替原来的分组变量du。vi为时间效应,代替dt,因而我们采用固定效应模型估计模型(1),就无法估计出du。如果按照模型(2)设定就为双向固定效应模型,其实在具体分析中,我们未必这么设定(见下文分析)。这就是为什么DID方法在一定程度上可以减轻遗漏变量带来的衡量偏误问题(消除了不可观测的非时变因素,同时估计模型时,还需要进一步加入控制变量)。
上述DID思想看起来并不复杂,主要在于DID稳健性检验,对于编程和技术细节处理要求较高(在实际分析中,我们经常会得到不理想的结果,这就需要本身的计量水平和技术处理了)。DID并不是只跑个简单回归就可以,需要严格的稳健性检验。稳健性检验可以参考上期推文。这里简单阐述下:
(1)共同趋势检验,对于多个不同政策时间点,推荐使用回归方法进行,画图可能无法实现。基本思想为,将政策实施前的年份虚拟变量与处理组虚拟变量交叉相乘,若果政策实施前的交互项并不显著,而双重差分项依然显著,就可以说明已经通过共同趋势假设检验。
(2)政策唯一性检验。寻找处理组(或所有个体)在政策年份附近其他政策(要有影响的政策,选择无关政策没有任何意义),加入该政策的虚拟变量或者重新构造双重差分项,加入原有模型进行回归即可。如果原有差分项项系数依然显著,但系数变小,就可以判断原来政策还是主要影响因素(最理想结果),其他情形结合结果分析即可。
(3)其他检验,见上一篇推文。部分文献中可以选取一个完全不受政策干预影响的因素作为被解释变量进行回归,双重差分项回归系数不显著最好,如果DID估计量的回归结果依然显著,说明原来的估计结果很有可能出现了偏误(不好的结果,不要报告论文中)。
当然稳健性检验还有很多方法,根据自己实证需要择优选择。
二、双重差分的局限性解决办法
个体之间会随时间表现出系统差异,同时宏观经济环境也随时间而变(时间效应),故政策实施地区的前后差异未必就是处理效应。为了克服这种样本选择偏差,可以使用倾向得分匹配模型(PSM)、广义倾向得分匹配模型(GPS)、广义精确匹配模型(CEM)进行匹配再验证。先匹配再DID,还是先DID,然后匹配再DID,两种方法都可以,根据你的数据和主题等比较选择。如果可以使用PSM可以分析影响因素,将其提前更好,如果侧重DID,PSM等匹配模型作为稳健性检验,可以选择后者。
特别地,
上期我们采用reg、xtreg、areg(linear regression with a largedummy-variable set)进行回归,其实估计结果是一样的。这说明只要模型设定合理,假设检验通过,不同的估计方法都可以得到想要的估计结果。当然这里面涉及到很多技术处理问题,本文就不再赘述。
三、多期双重差分
对于政策实施时间不一致的情况,可以采用构造的“多期双重差分方法”进行分析。一般而言,在多期DID模型中我们只需要关心交互项DID=treated*time(其实标准DID模型,一般也只关心交互项,不随时间改变的treated使用xtreg也无法得到估计值)。因此,建议使用混合最小二乘法进行估计,当然对于单一时间点的政策,在某些情况下,采用双向固定效应估计结果较好。使用混合最小二乘法的原因在于:政策在各个地区实施的时间跨度很大,导致用来估计的双重差分项观测值较少,存在一定的偏误。例如在分析《地铁修建可以提升区域一体化?》相关论文时,上海、北京等大城市修建地铁较早,而南昌修建地铁很晚(2015),而使用的数据为2005-2016年,那么南昌的只能有两年的treated=1,而采用固定效应等模型需要进行组内估计,这样显得观测值太少。因此,可以忽略panel data数据结构,而直接使用类似于repeated cross section的数据结构来进行DID回归。(相应的模型设定与估计方法参考上篇推文)
四、影响机制识别
DID交互项*其他变量可以进一步识别影响机制。例如分析地铁修建可以提升区域一体化?假设地铁修建是否可以从资源配置(source)、流动率(flow)等因素间接影响区域一体化(只是假设,为了说明问题)。此时,只需要将source与flow这两个变量与构建的双重差分项再次交叉相乘,同时将这两个变量加入回归方程进行回归就可以识别影响机制。这种机制检验构建的模型类似于三重差分方法(DDD)的表达式。
在分析的过程中,可能审稿专家还会说DID没有解决内生性问题,这时候可以使用工具变量进行进一步稳健性检验。可以采用ivreg2命令,该命令提供了2SLS与两阶段GMM估计方法。
五、三重差分方法(DDD)
@计量经济圈
我们现在想要研究香港推行的针对60岁以上的老年人的医保政策,假定该政策生效日期是2008年,那么我们想要知道是否这个医保政策促进了香港老年人的健康?每当看到这个的时,候我们首先需要问自己,这里面出现了几个有效信息。
从这个描述来看,我们能够得到三个有效信息:第一,该政策是在香港实行,第二,该政策是针对60岁以上老年人,第三,该政策生效日期是2008年。如果你发现有三个有效信息,一般而言,我们最好采用DDD三重
差分法
来更好地估计该医保政策的效果。标准的DID双重差分法,实际上是提供了两个有效信息:香港和2008,即在2008年香港执行该项医保政策,现在的情况是三个有效信息。
我们推演一下,为什么此处最好使用三重差分法来获得政策效应。如果不考虑其他没有执行该项政策的内陆省份的情况,直接用2008年之后香港60岁以上的老年人健康状况与2008年之前的香港60岁以上的老年人健康状况,那谁知道健康状况的变化是不是因为金融危机造成的,所以这里面的混淆因素就理不清楚了。这就是为什么我们需要把其他没有执行该医保政策的内陆省份包括进来作为控制组,来控制这些大环境因素造成的健康状况变化。
另外,如果直接用香港60岁以上老年人群体的健康状况(处理组)减去60岁以下中年人群体的健康状况(控制组),那有什么大的问题呢?我们压根分不清这个处理组与控制组健康状况差异到底是不是由于这个医保政策造成的,毕竟老年人和中年人群体的健康状况本来就存在系统性的差异。
标准的三重差分就像下面这个式子所展示的那样,他的变异形式就比较广了,只要有三个交互项的乘积在里面(DID*其他任何一个变量),都可以叫做三重差分。