26 个回答
在这里,我想借用垃圾邮件分类这个例子来简单描述朴素贝叶斯分类器。
首先根据已经标记好的邮件,即垃圾邮件与正常邮件,选择邮件中的一部分作为训练集,提取邮件中大多数重要的词语,建立词库。并统计每一个词语在垃圾邮件中出现的频率和在正常邮件中出现的频率,做好有关记录。
在这里,我们用S(Spam)表示垃圾邮件,H(Healthy)表示正常邮件。对于某个词语W(Word),P(W|S)即表示垃圾邮件中出现词语W的概率,在已经建立的词库中已知。P(W|H)即表示正常邮件中出现词语W的概率,在已经建立的词库中已知。
由Bayes公式易知出现词语W的邮件为垃圾邮件的概率为:
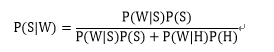
对于一封需要判别的邮件,我们提取其中的词语,并计算其中的每个词语的P(W|S)与P(W|H)。对于多个词语,选取P(W|S)最高的N个词语(N数值可以调整)。计算联合概率。令P_i=P(W_i |S),则有计算公式:
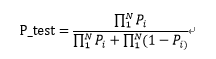
设定一个阈值P,若P_test>P,则判定为垃圾邮件。反之,判定为正常邮件。
那么,朴素贝叶斯分类器中的”朴素“从何而来呢?
原来,我们在训练模型的时候,由于训练集有限而垃圾邮件文本内容无限,不可能找到覆盖所有可能情况的训练集。所以将对文本的分析转换为对词或词的组合进行分析,也就是说不用句子作特征,而用句子中的词作特征。此时,我们就引入了简单粗暴可以说很“朴素”的条件独立假设来简化问题,即认为项与项之间独立,其对最终结果的贡献互不影响(注意这里指的是项与项之间互相独立,每一项可能代表一个词,即一元语言模型;也可能代表多个词,即n元语言模型)。
之前论智君编译过一篇 《6步骤带你了解朴素贝叶斯分类器(含Python和R语言代码)》 ,也许有用。
假设你正在处理一个分类问题,你已经形成了一些假设,建立了一套特征并且确定了各变量的重要性。你的数据集中有一大堆数据点,但是只有很少的变量,而你的上司希望你能在一小时内给出预测数据,你会怎么办?
如果我是你,我会用朴素贝叶斯分类器。相比较其他分类方法,朴素贝叶斯简单高效,适合预测未知类数据集。
在这篇文章中,我将解释该算法的基础知识,如果你是Python和R语言的新手,下次你遇到大型数据集,你就能学以致用。
什么是朴素贝叶斯分类器?
朴素贝叶斯分类器是一种基于贝叶斯定理的弱分类器,所有朴素贝叶斯分类器都假定样本每个特征与其他特征都不相关。举个例子,如果一种水果其具有红,圆,直径大概3英寸等特征,该水果可以被判定为是苹果。尽管这些特征相互依赖或者有些特征由其他特征决定,然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。
朴素贝叶斯分类器很容易建立,特别适合用于大型数据集,众所周知,这是一种胜过许多复杂算法的高效分类方法。
贝叶斯公式提供了计算后验概率P(X|Y)的方式:

其中,
- P(c|x)是已知某样本(c,目标),(x,属性)的概率。称后验概率。
- P(c)是该样本“c”的概率。称先验概率。
- P(x|c)是已知该样本“x”,该样本“c”的概率。
- P(x)是该样本“x”的概率。
朴素贝叶斯算法的分类流程
让我举一个例子。下面我设计了一个天气和响应目标变量“玩”的训练数据集(计算“玩”的可能性)。我们需要根据天气条件进行分类,判断这个人能不能出去玩,以下是步骤:
步骤1:将数据集转换成频率表;
步骤2:计算不同天气出去玩的概率,并创建似然表,如阴天的概率是0.29;
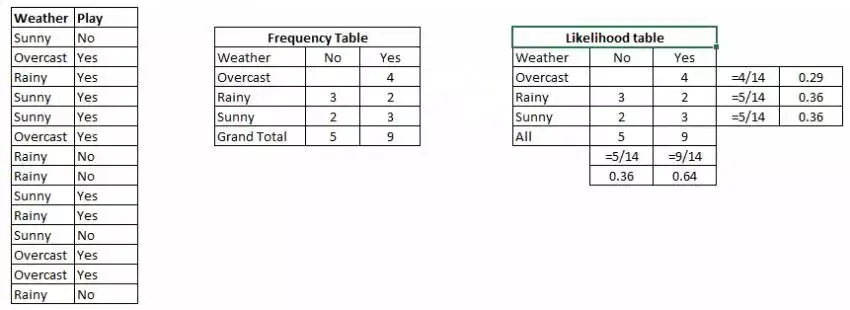
步骤3:使用贝叶斯公式计算每一类的后验概率,数据最高那栏就是预测的结果。
问题:如果是晴天,这个人就能出去玩。这个说法是不是正确的?
P(是|晴朗)=P(晴朗|是)×P(是)/P(晴朗)
在这里,P(晴朗|是)= 3/9 = 0.33,P(晴朗)= 5/14 = 0.36,P(是)= 9/14 = 0.64
现在,P(是|晴朗)=0.33×0.64/0.36=0.60,具有较高的概率。
朴素贝叶斯适合预测基于各属性的不同类的概率,因此在文本分类上有广泛应用。
朴素贝叶斯的优缺点
优点:
- 既简单又快速,预测表现良好;
- 如果变量独立这个条件成立,相比Logistic回归等其他分类方法,朴素贝叶斯分类器性能更优,且只需少量训练数据;
- 相较于数值变量,朴素贝叶斯分类器在多个分类变量的情况下表现更好。若是数值变量,需要正态分布假设。
缺点:
- 如果分类变量的类别(测试数据集)没有在训练数据集总被观察到,那这个模型会分配一个0(零)概率给它,同时也会无法进行预测。这通常被称为“零频率”。为了解决这个问题,我们可以使用平滑技术,拉普拉斯估计是其中最基础的技术。
- 朴素贝叶斯也被称为bad estimator,所以它的概率输出predict_proba不应被太认真对待。
- 朴素贝叶斯的另一个限制是独立预测的假设。在现实生活中,这几乎是不可能的,各变量间或多或少都会存在相互影响。
朴素贝叶斯的4种应用
实时预测 :毫无疑问,朴素贝叶斯很快。
多类预测 :这个算法以多类别预测功能闻名,因此可以用来预测多类目标变量的概率。
文本分类/垃圾邮件过滤/情感分析 :相比较其他算法,朴素贝叶斯的应用主要集中在文本分类(变量类型多,且更独立),具有较高的成功率。因此被广泛应用于垃圾邮件过滤(识别垃圾邮件)和情感分析(在社交媒体平台分辨积极情绪和消极情绪的用户)。
推荐系统 :朴素贝叶斯分类器和协同过滤结合使用可以过滤出用户想看到的和不想看到的东西。
如何建立朴素贝叶斯的基本模型(Python和R)
scikit learn里有3种朴素贝叶斯的模型:
高斯模型 :适用于多个类型变量,假设特征符合高斯分布。
多项式模型 :用于离散计数。如一个句子中某个词语重复出现,我们视它们每个都是独立的,所以统计多次,概率指数上出现了次方。
伯努利模型 :如果特征向量是二进制(即0和1),那这个模型是非常有用的。不同于多项式,伯努利把出现多次的词语视为只出现一次,更加简单方便。
你可以根据特定数据集选取上述3个模型中的合适模型。下面我们以高斯模型为例,谈谈怎么建立:
- Python
#Import Library of Gaussian Naive Bayes model
from sklearn.naive_bayes import GaussianNB
import numpy as np
#assigning predictor and target variables
x= np.array([[-3,7],[1,5], [1,2], [-2,0], [2,3], [-4,0], [-1,1], [1,1], [-2,2], [2,7], [-4,1], [-2,7]])
Y = np.array([3, 3, 3, 3, 4, 3, 3, 4, 3, 4, 4, 4])
#Create a Gaussian Classifier
model = GaussianNB()
# Train the model using the training sets
model.fit(x, y)
#Predict Output
predicted= model.predict([[1,2],[3,4]])
print predicted
Output: ([3,4])
- R
require(e1071) #Holds the Naive Bayes Classifier
Train <- read.csv(file.choose())
Test <- read.csv(file.choose())
#Make sure the target variable is of a two-class classification problem only
levels(Train$Item_Fat_Content)
model <- naiveBayes(Item_Fat_Content~., data = Train)
class(model)
pred <- predict(model,Test)
table(pred)
关于朴素贝叶斯分类器的几个黑科技
以下是一些小方法,可以提升朴素贝叶斯分类器的性能:
- 如果连续特征不是正态分布的,我们应该使用各种不同的方法将其转换正态分布。
- 如果测试数据集具有“零频率”的问题,应用平滑技术“拉普拉斯估计”修正数据集。
- 删除重复出现的高度相关的特征,可能会丢失频率信息,影响效果。
- 朴素贝叶斯分类在参数调整上选择有限。我建议把重点放在数据的预处理和特征选择。
- 大家可能想应用一些分类组合技术 如ensembling、bagging和boosting,但这些方法都于事无补。因为它们的目的是为了减少差异,朴素贝叶斯没有需要最小化的差异。
原回答:
考虑过滤垃圾邮件这个经典例子。
怎么过滤垃圾邮件?
最简单的分类方法,就是预先定义一些规则,例如发件人、关键词、发信服务器和声称的地址是否一致等。但是,这样预先设定的分类方法实际效果并不是很好。
因为预先定义完善的规则需要花费大量的精力,而且不同用户需要的规则也是不一样的。另外,从产品的角度来说,很多用户可能并不具备设定一个完善的规则的能力或者精力。
其次,在利益的驱使下,垃圾邮件的发送者会不断改进自身的系统。因此,预先定义的规则哪怕再完善,也会逐渐过时。
而通过机器学习,能“自行”学习哪些邮件是垃圾邮件,不需要预先设定完善的规则,也能随垃圾邮件的变化而变化,遇强则强。
就拿根据关键词过滤垃圾邮件来说吧。传统的做法是预先定义出现哪些关键词就判定为垃圾邮件。那这个做法面对千变万化的垃圾邮件显然会很无力。如果通过机器学习来过滤的话,那我们可以一方面统计某些词语在正常邮件和垃圾邮件中出现的频率,根据两者的不同推断一封新邮件是正常邮件还是垃圾邮件;另一方面,我们又可以利用推断的结果反过来推断某些词语在正常邮件和垃圾邮件中出现的频率。这样,这个系统分类的邮件越多,识别效果就越好。
抽象一下,我们根据历史数据统计某一特征
f
在分类
S
和
N
中出现的概率(
pSucc f S
和
pSucc f N
),据此推断新数据属于
S
还是
N
。同时,我们根据新数据的分类,推断分类为
S
和
N
的邮件具有特征
f
的概率(
pSucc S f
和
pSucc N f
),并进而调整
pSucc f S
和
pSucc f N
的值。
那么这个学习过程其实是辗转计算
pSucc f S
和
pSucc S f
这一组概率(
N
的情况同理)。
那
pSucc f S
和
pSucc S f
有什么关系呢?
我们尝试代入一个具体的例子来摸索一下。假设
f
代表邮件中出现了“正规发票”这个词,而
S
代表这封邮件是垃圾邮件。那么,直觉上,我们有:
- 包含“正规发票”这个词的邮件是垃圾邮件的概率越大,相应地,垃圾邮件中包含“正规发票”这个词的概率也越大
- 包含“正规发票”这个词的邮件是垃圾邮件的概率和垃圾邮件中包含“正规发票”这个词的概率并不相等
- 包含“正规发票”这个词的邮件是垃圾邮件的概率大于垃圾邮件中包含“正规发票”这个词的概率
抽象上述表述,我们得到:
pSucc f S = coefficient * (pSucc S f) -- coefficient > 0
pSucc f S /= pSucc S f


