三角不等式Triangle Inequality


我们在中学就知道平面几何中著名的三角不等式:三角形两边之和大于第三边,即 z\leq x+y 。只有当三角形蜕化为三边共线时,才有机会取等号。
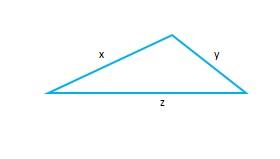
三角不等式在欧式几何中,可以用矢量和它们的距离来表达: \color{blue}{||\vec{x}+\vec{y}||\leq ||\vec{x}||+||\vec{y}||} ,上述三角不等式中第三边的边长 z 变成了 ||\vec{x}+\vec{y}|| ,其中 ||\vec{.}|| 就是我们最熟悉的矢量的长度的定义(在 \mathbb{R^{2}},\mathbb{R^{3}} 中这个矢量版本的三角不等式很直观)。矢量蜕化到 \mathbb{R^{1}} 中就变成了实数,于是有另一个版本的三角不等式: \color{blue}{|x+y|\leq|x|+|y|} 。
现在我们来证明实数版本的三角不等式: |x+y|\leq|x|+|y| 。
证: 证明绝对值不等式经常会用到这个恒等式: -|a|\leq a\leq |a| 。 所以上式可以写成 -|x|\leq x\leq |x|,-|y|\leq y\leq |y| 。两式相加得到 -|x|-|y|\leq x+y\leq |x|+|y| 。再根据绝对值的性质“当 a>0 时, -a\leq x\leq a\Leftrightarrow |x|\leq a “,就得到 |x+y|\leq|x|+|y| 。
由 |x+y|\leq|x|+|y| 可以得到:
- 取 x=a-b,y=b-c ,有 |a-c|<|a-b|+|c-b| 。
- |x-y|\leq |x|+|y|
- |x|-|y|\leq|x-y|
- ||x|-|y||\leq|x-y|
可以自己试试证明它们。
我们再来证明一下矢量版本的三角不等式 ||\vec{x}+\vec{y}||\leq ||\vec{x}||+||\vec{y}|| 。
证: ||\vec{x}+\vec{y}||^{2}=(\vec{x}+\vec{y})\cdot(\vec{x}+\vec{y}) =\vec{x}\cdot\vec{x}+2\vec{x}\cdot\vec{y}+\vec{y}\cdot\vec{y} =||\vec{x}||^{2}+2\vec{x}\cdot\vec{y}+||\vec{y}||^{2} \color{red}{\leq^{*}} ||\vec{x}||^{2}+2||\vec{x}||||\vec{y}||+||\vec{y}||^{2} =(||\vec{x}||+||\vec{y}||)^{2} ,即 ||\vec{x}+\vec{y}||\leq ||\vec{x}||+||\vec{y}|| 。
\color{red}{\leq^{*}} 这一步用到了另一个著名的不等式柯西-施瓦兹不等式Cauchy-Schwarz Inequality(参考:《 柯西-施瓦兹不等式Cauchy-Schwarz Inequality 》)。
