转载自:
http://blog.csdn.net/lsldd/article/details/41251583
做回归分析,常用的误差主要有均方误差根(RMSE)和R-平方(R2)。
RMSE是预测值与真实值的误差平方根的均值
。这种度量方法很流行(Netflix机器学习比赛的评价方法),是一种定量的权衡方法。
””’ 均方误差根 ”’
def rmse(y_test, y):
return sp.sqrt(sp.mean((y_test - y) ** 2))
R2方法是将预测值跟只使用均值的情况下相比,看能好多少
。其区间通常在(0,1)之间。0表示还不如什么都不预测,直接取均值的情况,而1表示所有预测跟真实结果完美匹配的情况。
””’ 与均值相比的优秀程度,介于[0~1]。0表示不如均值。1表示完美预测. ”’
def R2(y_test, y_true):
return 1 - ((y_test - y_true)**2).sum() / ((y_true - y_true.mean())**2).sum()
本例中使用一个2次函数加上随机的扰动来生成500个点,然后尝试1、2、100次方的多项式对该数据进行拟合。拟合的目的是使得根据训练数据能够拟合出一个多项式函数,这个函数能够很好的拟合现有数据,并且能对未知的数据进行预测,拟合结果如下:
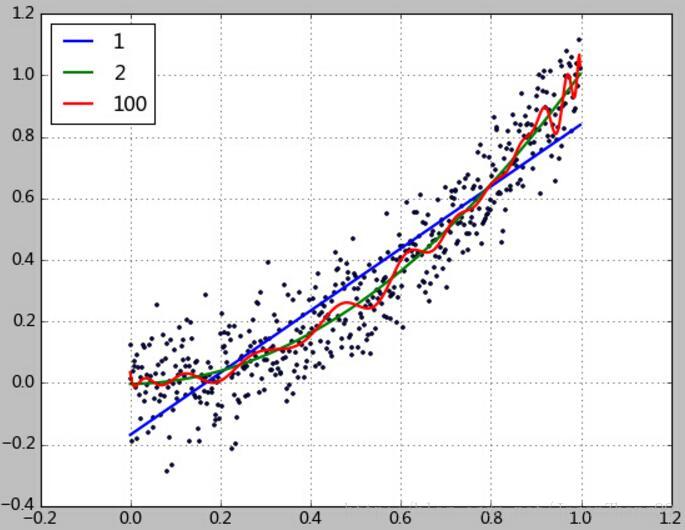
1次项系数:[-0.16140183 0.99268453] rmse=0.13, R2=0.82, R22=0.58, clf.score=0.82
2次项系数:[ 0.00934527 -0.03591245 1.03065829] rmse=0.11, R2=0.88, R22=0.66, clf.score=0.88
100次项:rmse=0.10, R2=0.89, R22=0.67, clf.score=0.89
使用100次方多项式做拟合,效果确实是高了一些,然而该模型的据测能力却极其差劲,模型产生了过拟合。
而且注意看多项式系数,出现了大量的大数值,甚至达到10的12次方。
将500个样本中的最后2个从训练集中移除。然而在测试中却仍然测试所有500个样本,拟合结果如下:
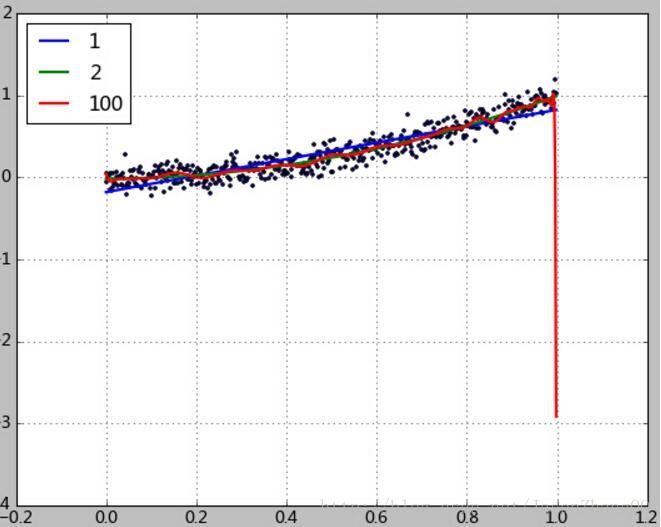
1次项系数:[-0.17933531 1.0052037 ] rmse=0.12, R2=0.85, R22=0.61, clf.score=0.85
2次项系数:[-0.01631935 0.01922011 0.99193521] rmse=0.10, R2=0.90, R22=0.69, clf.score=0.90
100次项:rmse=0.21, R2=0.57, R22=0.34, clf.score=0.57
仅仅只是缺少了最后2个训练样本,红线(100次方多项式拟合结果)的预测发生了剧烈的偏差,R2也急剧下降到0.57。
这说明高次多项式过度拟合了训练数据,包括其中大量的噪音,导致其完全丧失了对数据趋势的预测能力。前面也看到,100次多项式拟合出的系数数值无比巨大。人们自然想到通过在拟合过程中限制这些系数数值的大小来避免生成这种畸形的拟合函数。
其基本原理是将拟合多项式的所有系数绝对值之和(L1正则化)或者平方和(L2正则化)加入到惩罚模型中,并指定一个惩罚力度因子w,来避免产生这种畸形系数。
这样的思想应用在了岭(Ridge)回归(使用L2正则化)、Lasso法(使用L1正则化)、弹性网(Elastic net,使用L1+L2正则化)等方法中,都能有效避免过拟合,下面使用L2正则化岭回归拟合结果:
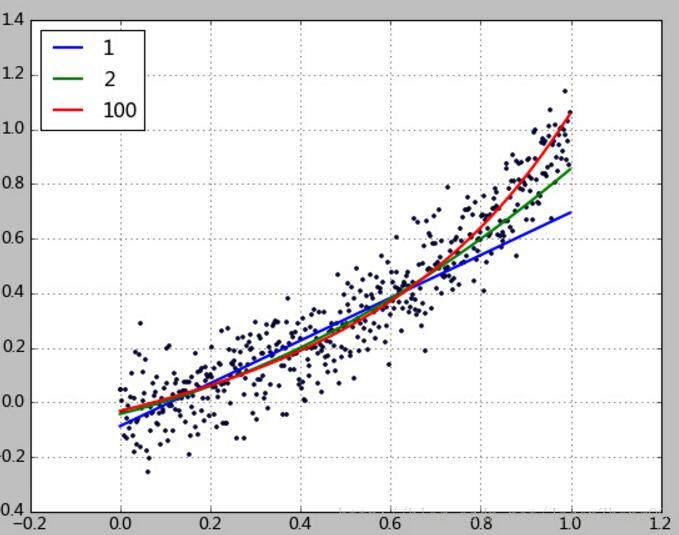
做回归分析,常用的误差主要有均方误差根(RMSE)和R-平方(R2)。RMSE是预测值与真实值的误差平方根的均值。这种度量方法很流行(Netflix机器学习比赛的评价方法),是一种定量的权衡方法。 ””’ 均方误差根 ”’ 过拟合加入L1正则化和L2正则化,岭回归
误差越大,该值越大。
SSE(和方差)与MSE之间差一个系数n,即SSE = n * MSE,二者效果相同。
3.
均方根误差
(Root Mean Square Error,
RMSE
)
是MSE的算数平均
根
误差越大,该值越大。
4.平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)
注意:当真实值有数据等
写文章时候可以选用一下几个
1、
均方误差
:MSE(Mean Squared Error)
2、
均方根误差
:
RMSE
(Root Mean Squard Error)
RMSE
=sqrt(MSE)。
3、平均绝对误差:MAE(Mean Absolute Error)
4、决定系数:
R2
(R-Square)
一般来说,R-Squared 越大,表示模型拟合效果越好。R-Squared 反映的是大概有多准,...
误差越大,该值越大。
SSE(和方差)与MSE之间差一个系数n,即SSE = n * MSE,二者效果相同。
3.
均方根误差
(Root Mean Square Error,
RMSE
)
是MSE的算数平均
根
误差越大,该值越大。
4.平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)
注意:当真实值有数据等
# 定义MAPE
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred - y_true) / y_true)) * 100
# MSE
print(metrics.mean_squared_error(y_true, y_pred))
#
RMSE
print(np.sqrt(metrics.mean_squared_err...
Hadoop启动dfs时报错Incorrect configuration: namenode address dfs.namenode.servicerpc-address or dfs.namen
Java集合框架详解之继承list接口
WgRui:
Hadoop启动dfs时报错Incorrect configuration: namenode address dfs.namenode.servicerpc-address or dfs.namen
璐璐今天学习了吗:
在HDFS中创建目录报错WARN util.NativeCodeLoader: Unable to load native-hadoop library for your pla
Ahaxian:
回归评价指标:均方误差根(RMSE)和R平方(R2)


