卡尔曼估计实际由两个过程组成:预测与校正,在预测阶段,滤波器使用上一状态的估计,做出对当前状态的预测。在校正阶段,滤波器利用对当前状态的观测值修正在预测阶段获得的预测值,以获得一个更接进真实值的新估计值。
1、变量说明
 :卡尔曼估计值
:卡尔曼估计值
 :卡尔曼估计误差协方差矩阵
:卡尔曼估计误差协方差矩阵
 :预测误差协方差矩阵
:预测误差协方差矩阵
 :卡尔曼增益
:卡尔曼增益
 :测量余量
:测量余量
2、卡尔曼滤波器计算过程
更新协方差估计:
观察以上六个式子,我们使用过程中关键要明白
 ,
,
 的算法原理,及
的算法原理,及
 的更新算法
的更新算法
3、卡尔曼滤波算法详细推导
从协方差矩阵开始说起,真实值与预测值之间的误差为
预测误差协方差矩阵为
![{P}'_k=E[{e}'_k{e}'_k^T]=E[(x_k-\hat{x}'_k)(x_k-\hat{x}'_k)^T]](https://private.codecogs.com/gif.latex?%7BP%7D%27_k%3DE%5B%7Be%7D%27_k%7Be%7D%27_k%5ET%5D%3DE%5B%28x_k-%5Chat%7Bx%7D%27_k%29%28x_k-%5Chat%7Bx%7D%27_k%29%5ET%5D)
真实值与估计值之间的误差为
卡尔曼估计误差协方差矩阵为
将
 代入得到
代入得到
其中
![E[v_kv_k^T]=R](https://private.codecogs.com/gif.latex?E%5Bv_kv_k%5ET%5D%3DR) ,并将预测误差协方差矩阵代入,得到
,并将预测误差协方差矩阵代入,得到
卡尔曼滤波本质是最小均方差估计,而均方差是
 的迹,将上式展开并求迹
的迹,将上式展开并求迹
最优估计
 使
使
 最小,所以上式两边对
最小,所以上式两边对
 求导
求导
套用第一节中提到的那两个矩阵微分公式,得到
令上式等于0,得到
到此,我们就知道了卡尔曼增益是怎么算出来的了,但是又有问题,
 是怎么算的呢?
是怎么算的呢?
总结卡尔曼滤波的更新过程为
1步,首先
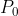 ,
,
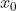 已知,然后由
已知,然后由
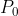 算出
算出
 ,再由
,再由
 算出
算出
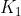 ,有了这些参数后,结合观测值就能估计出
,有了这些参数后,结合观测值就能估计出
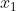 ,再利用
,再利用
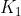 更新
更新
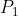
2步,然后下次更新过程为由
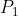 算出
算出
 ,再由
,再由
 算出
算出
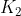 ,有了这些参数后,结合观测值就能估计出
,有了这些参数后,结合观测值就能估计出
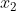 ,再利用
,再利用
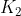 更新
更新
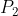
......
n步,由
 算出
算出
 ,再由
,再由
 算出
算出
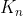 ,有了这些参数后,结合观测值就能估计出
,有了这些参数后,结合观测值就能估计出
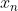 ,再利用
,再利用
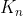 更新
更新
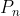
这就是卡尔曼滤波器递推过程。
至于
 的算法,
的算法,
将
 代入上式右边最后一项中 ,
代入上式右边最后一项中 ,
 保持原样
保持原样
网上搜索有关
卡
尔
曼
滤波
器中P,Q,R矩阵的设置,感觉讲述得比较笼统。又因为我要使用雷达目标跟踪方面使用
卡
尔
曼
滤波
器,因此针对雷达中目标匀速运动的情况来说明一下P,Q,R矩阵的设置。
本文来自公众号“——————目标跟踪中,在数据关联后往往要进行
卡
尔
曼
滤波
。数据关联
算法
得到了每个目标的观测数据。
卡
尔
曼
滤波
使用关联的观测数据来估计目标的状态,并预测目标的未来位置和速度等信息。目标跟踪过程中,测量数据通常会受到各种噪声的影响,例如传感器噪声、环境干扰等。
卡
尔
曼
滤波
器可以通过对测量数据和系统模型的加权处理来减少噪声的影响,提供更准确的目标状态估计。1、
卡
尔
曼
滤波
简介
卡
尔
曼
滤波
用来估计带噪信号中隐藏的真实信息。
目录1.
卡
尔
曼
滤波
入门2.学
卡
尔
曼
滤波
的必备知识2.1.状态空间表达式2.2.高斯分布2.3.方差2.4.超参数2.5.
卡
尔
曼
直观图解3.
卡
尔
曼
滤波
3.1.
卡
尔
曼
公式理解3.2.调节超参数3.2.1.Q和R的取值3.2.2.P0和X0的取值3.2.3.
卡
尔
曼
滤波
的使用...
1. 概率论相关知识
这一节主要叙述概率论的一些相关基础知识,包括全概率公式、贝叶斯公式、协方差矩阵、二维高斯分布等等,对这些熟悉的可以直接跳到第二节
1.1 全概率公式与贝叶斯公式
1.2 协方差矩阵
1.3 二维高斯分布
2. 贝叶斯(Bayes)
滤波
卡
尔
曼
滤波
是基于贝叶斯
滤波
的一种改进,这里先说明一下贝叶斯
滤波
的相关原理。
2.1 变量定义
运动过程一般需要用到的变量主要有3个:
xi\boldsymbol x_ixi表示iii时刻的状态。比如在运动的机器人中,表示机器人当前的位姿
zi\bold
本教程来源于bibili up主DR_CAN的笔记整理,建议读者配合视频食用,视频链接如下:【
卡
尔
曼
滤波
器】1_递归
算法
_Recursive Processing_哔哩哔哩_bilibili在此非常感谢DR_CAN老师精彩讲解,在此表示崇高的敬意。
卡
尔
曼
滤波
算法
实际是一个观测器,可以用来估计下一个状态,具有非常好的实时性。其公式为:假定我们要对一个未知长度的物体进行测量,每次的测量值为ZkZ_kZk,取前kkk次的平均值作为当前的估计值(最优估计),则可得到以下公式:xk^=Z1+Z2+....+Zkk=
状态是指在系统中可决定系统状态、最小数目变量的有序集合。 而所谓状态空间则是指该系统全部可能状态的集合。
状态空间表示法
即为一种将物理系统表示为一组输入、输出及状态的数学模式,而输入、输出及状态之间的关系可用许多一阶微分方程来描述。
为了使数学模式不受输入、输出及状态的个数所影响,输入、输出及状态都会以向量的形式表示,而微分方程(若是线性非时变系统,可将微分方程转变为代数方程)则会以矩阵的形式来来表示。
状态转移矩阵 (转移概率矩阵)
状态转移是指客观事物由一种状态转
什么是
卡
尔
曼
滤波
?
对于这个
滤波
器,我们几乎可以下这么一个定论:只要是存在不确定信息的动态系统,
卡
尔
曼
滤波
就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰,
卡
尔
曼
滤波
通常也能很好的弄清楚究竟发生了什么,找出现象间不易察觉的相关性。
因此
卡
尔
曼
滤波
非常适合不断变化的系统,它的优点还有内存占用较小(只需保留前一个状态)、速度快,是实时问题和嵌入式系统的理想选择。
如果你曾经Goog...