红黑树:这是一颗会自动调整树形态的树结构,比如当二叉树处于一个不平衡状态时,红黑树就会自动左旋右旋节点以及节点变色,调整树的形态,使其保持基本的平衡状态(时间复杂度为 O(logn)),也就保证了查找效率不会明显减低。
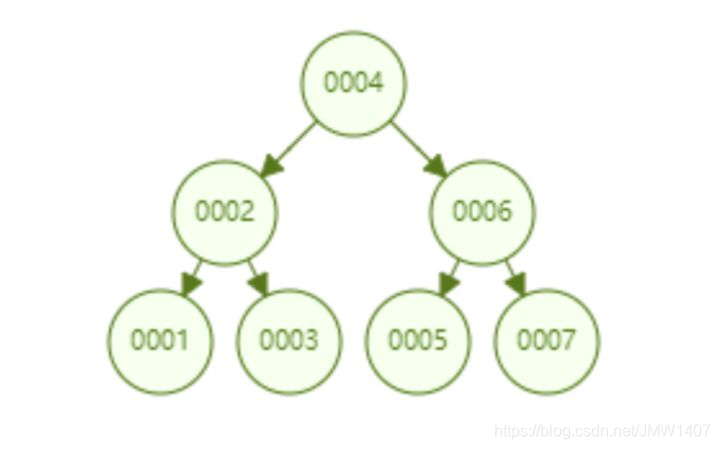
比如从 1 到 7升序插入数据节点,如果是普通的二叉查找树则会退化成链表,但是红黑树则会不断调整树的形态,使其保持基本平衡状态。如下图所示。下面这个红黑树下查找 id=7 的所要比较的节点数为 4,依然保持二叉树不错的查找效率。
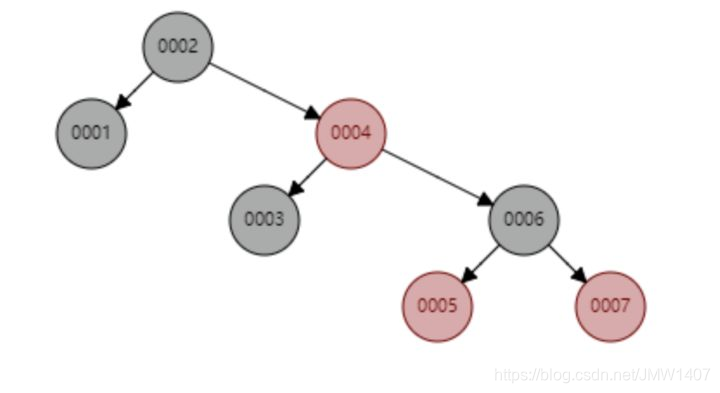
不足之处
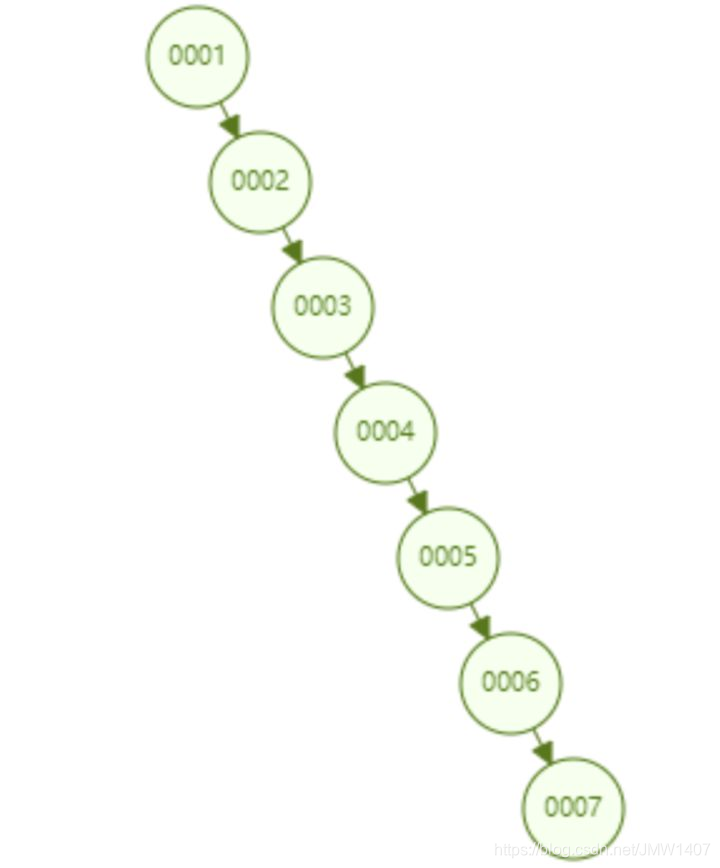
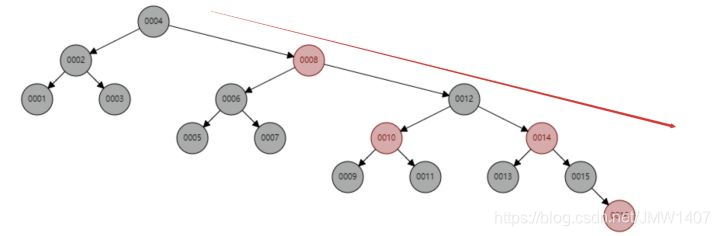
红黑树顺序插入 1~16 个节点,查找 id=16 需要比较的节点数为 6 次。
观察一下这个树的形态,是不是当数据是顺序插入时,树的形态一直处于“右倾”的趋势呢?
从根本上上看,红黑树并没有完全解决二叉查找树虽然这个“右倾”趋势,虽然没有二叉查找树退化为线性链表那么夸张,但是数据库中的基本主键自增操作,主键一般都是数百万数千万的,效率也很低。
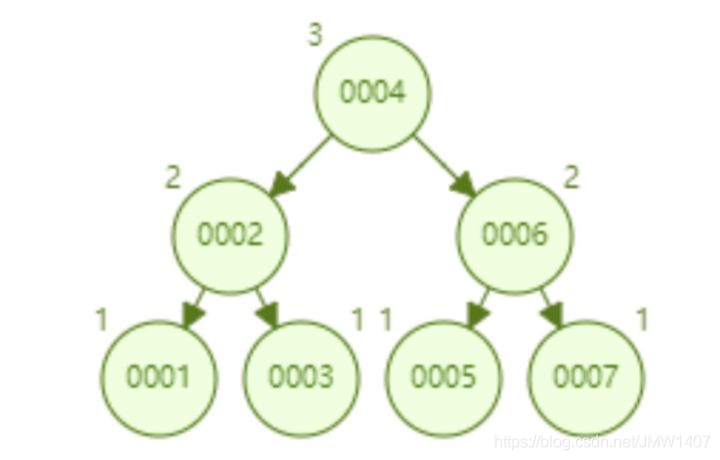
AVL 树:自平衡二叉树 。因为 AVL 树是个绝对平衡的二叉树,左右子树高度差小于等于1
- 因此在调整二叉树的形态上消耗的性能会更多。当树的某个位置被删除节点,需要经过一系列左旋右旋操作维持高度平衡。
- 查找性能(
O(logn)),不存在极端的低效查找的情况
AVL 树顺序插入 1~7 个节点,查找 id=7 所要比较节点的次数为 3。
AVL 树顺序插入 1~16 个节点,查找 id=16 需要比较的节点数为 4。
- 从查找效率而言,AVL 树查找的速度要高于红黑树的查找效率(AVL 树是 4 次比较,红黑树是 6 次比较)。
- 从树的形态看来,AVL 树不存在红黑树的“右倾”问题。
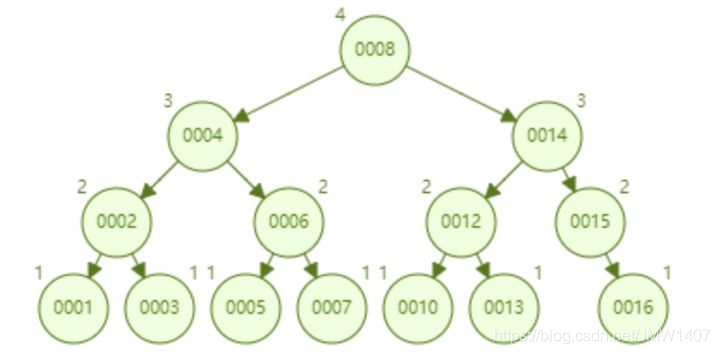
不足之处
数据库查询数据的瓶颈在于磁盘 IO,就是从磁盘读取 1B 数据和 1KB 数据所消耗的时间是基本一样的。
AVL 树的每一个树节点只存储了1个数据,我们一次磁盘 IO 只能取出来一个节点上的数据加载到内存里,那比如查询 id=7 这个数据我们就要进行磁盘 IO 三次,这是多么消耗时间的。设计数据库索引时首先考虑怎么减少磁盘 IO 的次数。
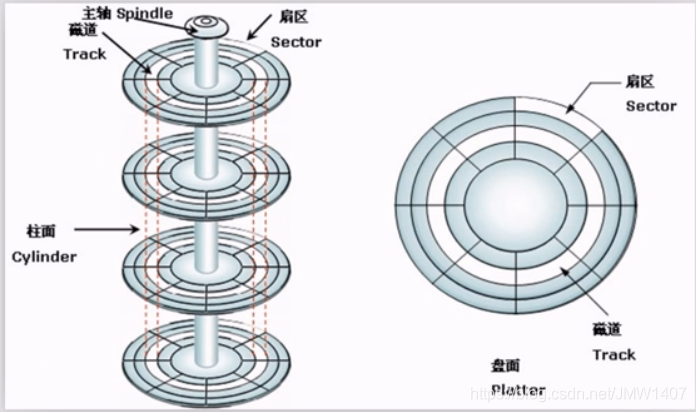
磁盘结构:
综上所述:
BST、红黑树、AVL突出的问题,我们需要维持基本结构平衡、需要考虑树的深度过深,可以在一个树节点上尽可能多地存储数据,一次磁盘 IO 就多加载点数据到内存,这就是 B 树,B+树的的设计原理了。
1、树的高度决定:因为B+树节点不放数据,所以可以存放更多的索引节点
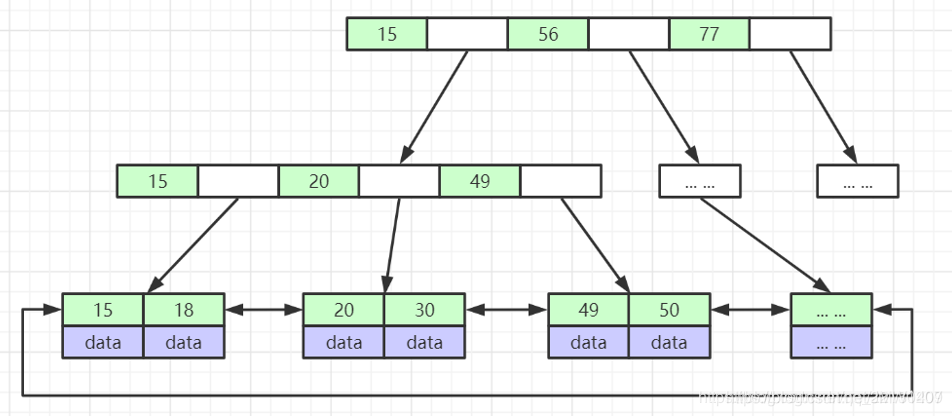
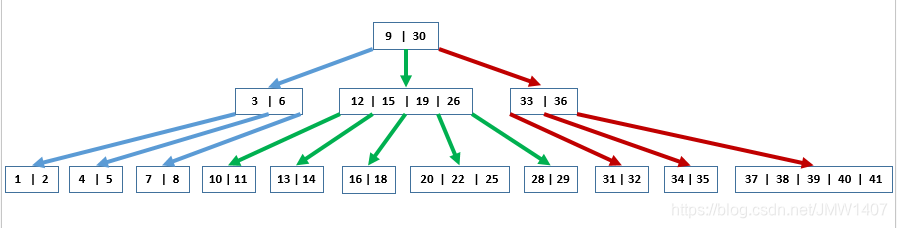
上图是B+树的结构:
mysql认为每个结点就是1个页,默认1页的大小是16KB。那么我们可以估算下3层高度能存储多少数据。
一张表假设用bigint做主键,8B大小,1个地址大概是6B。那么1页是16KB,可以存放16KB/14B=1170个结点。第二层同理1170个,那么叶子结点,最多也就1KB,这个叶结点16个。那么一共放1170x1170x16=2190万。这样的数据量也就用了3行。经过了3次磁盘IO就找到了元素。
mysql会把根节点常驻内存,那就更快了。高版本会把所有非叶子结点加载到内存,那么可能也就1次磁盘IO把叶子结点加到内存。
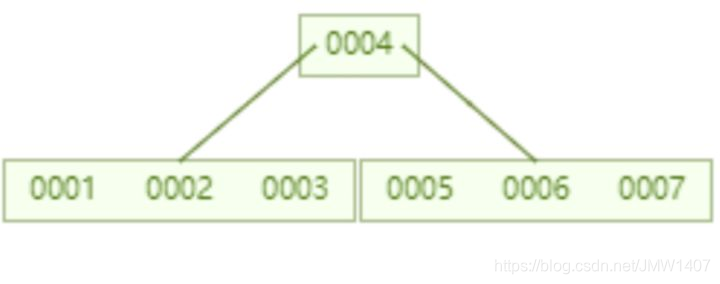
这是B树的本来样子,每个索引位置存放你想要的数据,可想而知每个节点字节很更大
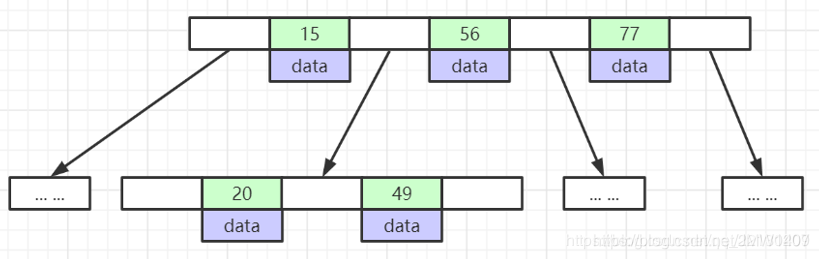
我们估算B树存储2000多万数据得多高?
每个结点16个元素,默认每个结点还是16KB,1个结点1KB大小,16/1 = 16,16^7 = 268 435 456,可以看到存储相同数据量,B+树仅用3层,B树最少7层。
2、B+树可以很好的支持范围查找
假设我们找大于20小于50范围内的数据,从根节点出发,找到叶子结点的20,沿着指针方向找到50就可以了。
B树没有指针,找完20,会继续从根节点往下找,效率会低得多。
哈希算法:也叫散列算法,就是把任意值(key)通过哈希函数变换为固定长度的 key 地址,通过这个地址进行具体数据的数据结构。adddress = f(key)
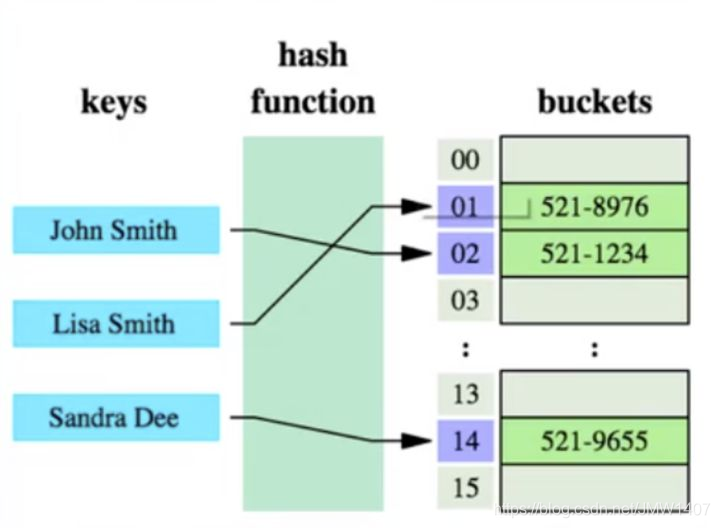
哈希算法首先计算存储 id=7 的数据的物理地址 addr=hash(7)=4231,而 4231 映射的物理地址是 0x77,0x77 就是 id=7 存储的额数据的物理地址,通过该独立地址可以找到对应 user_name='g'这个数据。这就是哈希算法快速检索数据的计算过程。
算法时间复杂度分析来看,哈希算法时间复杂度为 O(1),检索速度非常快。
不足之处1:哈希冲突
哈希函数可能对不同的 key 会计算出同一个结果,比如 hash(7)可能跟 hash(199)计算出来的结果一样。
常见处理方式:拉链法,即用链表把碰撞的数据接连起来。计算哈希值之后,还需要检查该哈希值是否存在碰撞数据链表,有则一直遍历到链表尾,直达找到真正的 key 对应的数据为止。
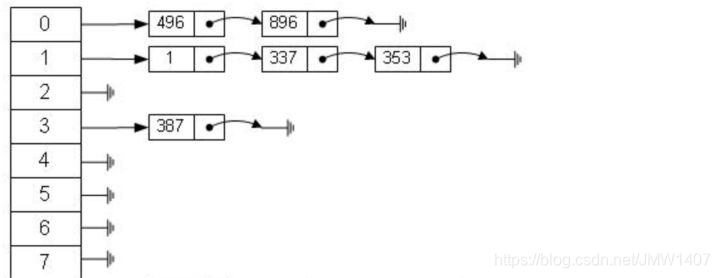
不足之处2:范围查找(致命之处)
用哈希算法实现的索引,范围查找怎么做呢?
简单的思路:一次把所有数据找出来加载到内存,然后再在内存里筛选筛选目标范围内的数据。但是这个范围查找的方法也太笨重了,没有一点效率而言。
InnoDB 是聚集索引方式,因此数据和索引都存储在同一个文件里。
- InnoDB 会根据
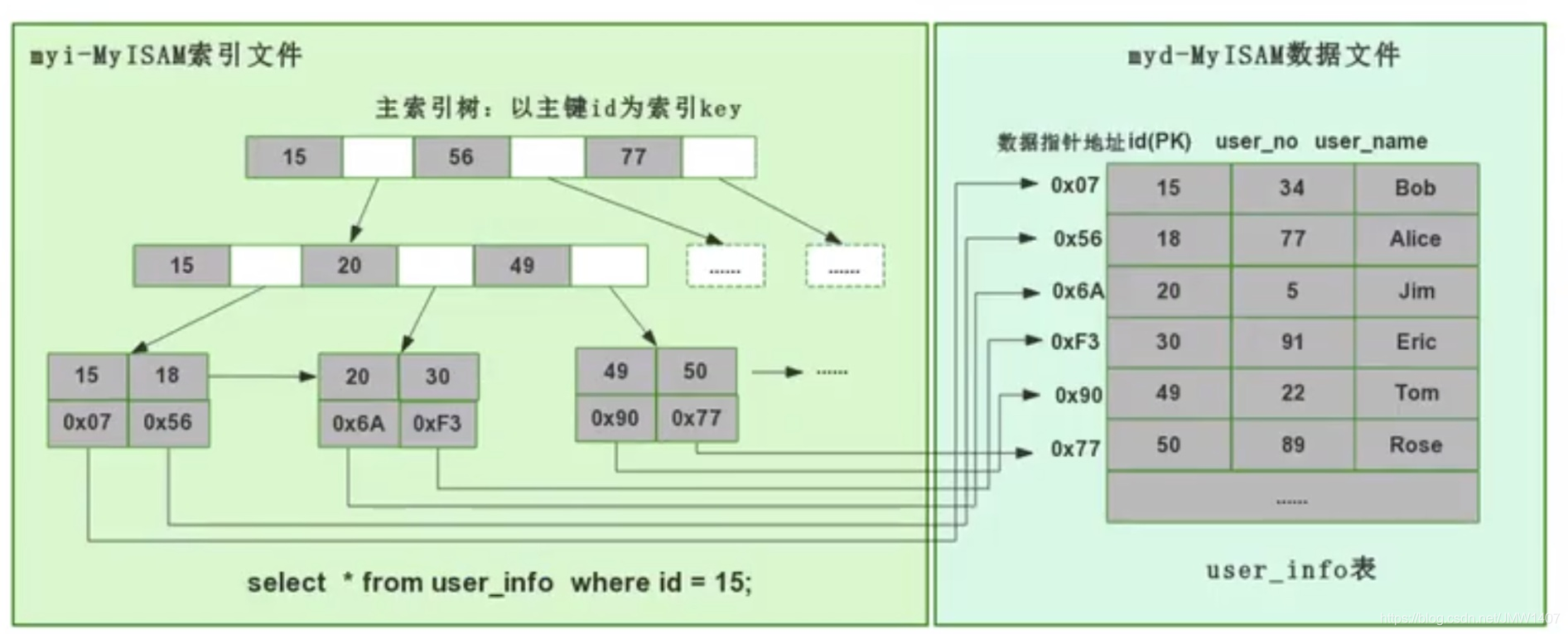
主键 ID 作为 key 建立索引 B+树,如左下图所示,而 B+树的叶子节点存储的是主键 ID 对应的数据,
- 比如在执行
select * from user_info where id=15 这个语句时,InnoDB 就会查询这颗主键 ID 索引
B+树,找到对应的 user_name='Bob'。
1、当我们为表里某个字段加索引时 InnoDB 会怎么建立索引树呢?
比如我们要给 user_name 这个字段加索引:
InnoDB 会建立 user_name 索引 B+树,节点里存的是 user_name 这个 KEY,叶子节点存储的数据的是主键 KEY。
叶子存储的是主键 KEY!!!拿到主键 KEY 后,InnoDB 才会去主键索引树里根据刚在 user_name 索引树找到的主键 KEY查找到对应的数据。
2、为什么 InnoDB 只在主键索引树的叶子节点存储了具体数据,但是其他索引树却不存具体数据呢,而要多此一举先找到主键,再在主键索引树找到对应的数据呢?
- 因为 InnoDB 需要节省存储空间。一个表里可能有很多个索引,InnoDB都会给每个加了索引的字段生成索引树,如果每个字段的索引树都存储了具体数据,那么这个表的索引数据文件就变得非常巨大(数据极度冗余了)。
- 从节约磁盘空间的角度来说,真的没有必要每个字段索引树都存具体数据,通过这种看似“多此一举”的步骤,在牺牲较少查询的性能下节省了巨大的磁盘空间,这是非常有值得的。
3、 MyISAM 查询性能比 InnoDB 更高?
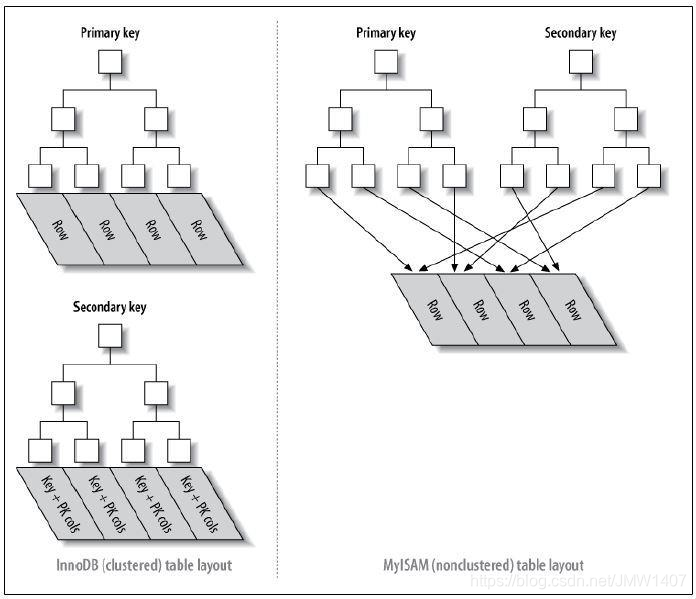
聚簇索引(InnoDB)
- 辅助索引的叶子节点的data存储的是主键的值;
- 主索引的叶子节点的data存储的是数据本身,也就是说数据和索引存储在一起;
- 索引查询到的地方就是数据(data)本身,那么索引的顺序和数据本身的顺序就是相同的;
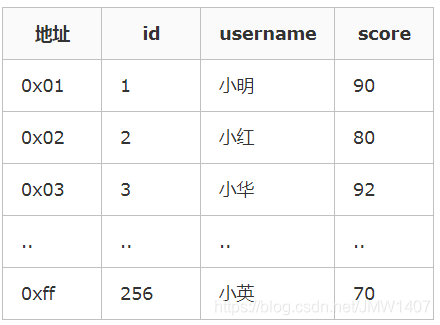
非聚簇索引(MyISAM )
主索引和辅助索引的叶子节点的data都是存储的数据的物理地址,也就是说索引和数据并不是存储在一起的,数据的顺序和索引的顺序并没有任何关系,也就是索引顺序与数据物理排列顺序无关。
综上特点:
- MyISAM 直接找到物理地址后就可以直接定位到数据记录;
- InnoDB 查询到叶子节点后,还需要再查询一次主键索引树,才可以定位到具体数据。
- 等于 MyISAM 一步就查到了数据,但是 InnoDB 要两步,那当然 MyISAM 查询性能更高。