如果判断点是否在凸多边形内，则有多种方法，方法简单，计算速度也快，直接使用物理引擎做判断也行
但实际问题中遇到的多边形不一定是凸多边形,它可能是凹边行或者复合多边形判断一个点在多边形内或多边形外，射线法是个不错的选择

射线法： ，判断一点是否在多边形内或多边形外，只要从这点起，作一条射线，例如，沿x(或y)向直到负无穷，若与其相交的边是奇，该点位于多边形内；若为偶数，则点位于多边形外。
如下图：

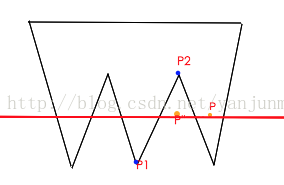
图中，沿P作水平向左的射线，若P在多边形内部，则射线与多边形的交点数为奇数；若P在多边形外部，则交点个数为偶数（包含0）。因此，顺序考虑多边形的每条边，求出交点数目，可判断点是否位于多边形内。特殊情况。如边(P1,P2)：
1)若射线恰好穿过P1或者P2,那么这个交点会被算作2次，解决方案是，若P的纵坐标与P1,P2中的纵坐标相同，则将忽略此情况
2)若射线水平，则射线可能与其无交点，可能有无数个，则忽略此情况。
3)若射线竖直，且P的横坐标小于P1,P2的横坐标，则必然相交。
4)在判断相交之前，可先判断P是否在边(P1,P2)的上面，若在，可直接得到结论：P在多边形内部

计算x轴坐标

计算交点逻辑

tanα = b /  c;
tanα = d / a;
d = b*a / c;

今天下午偶然瞄了一眼编程之美, 看到了一个问题, 4.4 点 是否 在 多边形 内. 为什么关注这个问题呢? 因为在今年给中科院保送研究生机试出题的时候,我也出了一道这样的题目. 看了编程之美的解答之后, 感觉作者没有把这个问题讲清楚, 所以来写这样一个东西. <编程之美>的两种解答方案都很直观, 一种是 秦九韶海伦公式来做面积 判断 , 一种是 常用的 判断 点 是否 在三角形内. 为什么说... 面积和判别法： 判断 目标 点 与 多边形 的每条边组成的三角形面积和 是否 等于该 多边形 ，相等则在 多边形 内部。 夹角和判别法： 判断 目标 点 与所有边的夹角和 是否 为360度，为360度则在 多边形 内部。 引射线法：从目标 点 出发引一条射线，看这条射线和 多边形 所有边的交 点 数目。如果有奇数个交 点 ，则说明在内部，如果有偶数个交 点 ，则说明在外部 首先讲解下射线法的原理 情况一，显示了具有 14 条边的严重 凹 陷 多边形 的典型情况 上图 显示了具有 14 条边的严重 凹 陷 多边形 的典型情况 红 点 是需要 （1）面积和判别法： 判断 目标 点 与 多边形 的每条边组成的三角形面积和 是否 等于该 多边形 ，相等则在 多边形 内部。 （2）夹角和判别法： 判断 目标 点 与所有边的夹角和 是否 为360度，为360度则在 多边形 内部。 （3）引射线法：从目标 点 出发引一条射线，看这条射线和 多边形 所有边的交 点 数目。如果有奇数个交 点 ，则说明在内部，如果有偶数个交 点 ，则说明在外部。 本文介绍的是引射... 在GIS（地理信息管理系统）中， 判断 一个坐标 是否 在 多边形 内部是个经常要遇到的问题。乍听起来还挺复杂。根据W. Randolph Franklin 提出的PNPoly算法，只需区区几行代码就解决了这个问题。 假设 多边形 的坐标存放在一个数组里，首先我们需要取得该数组在横坐标和纵坐标的最大值和最小值，根据这四个 点 算出一个四边型，首先 判断 目标坐标 点 是否 在这个四边型之内，如果在这个四边型之外，那可以... 我们先 判断 一个 点 是否 在一个三角形内部。一个三角形在一个坐标系（譬如由A、B、C三 点 组成）中，我们可以通过计算它的有向面积来 判断 A、B、C三 点 在坐标系中的顺逆。当然，在此之前我们必须先订立一套计算面积的规则。比如，在笛卡尔坐标系中，我们利用： S=((A.x-B.x)*(A.y+B.y)+(B.x-C.x)*(B. 将 多边形 划分为若干区域，二分地去查询落在哪个子区域， 判断 是落在哪个子区域内后 判断 是否 落在该区域的三角形内，若是则在 多边形 内，若不是则在 多边形 外。同上面三角形的 判断 方法一样，对凸 多边形 逆时针取向量，那么P 点 必然在这些向量的左侧。同上面三角形的 判断 方法一样，可以将 点 P与 多边形 所有顶 点 连线构成子三角形， 判断 这些子三角形的面积之和 是否 等于 多边形 面积之和。同上面三角形的 判断 方法一样，将 多边形 划分成若干三角形，然后用重心坐标性质 判断 。将P 点 与 多边形 各个顶 点 连线，环绕 多边形 一周，内角和为360°说明在 多边形 内。... 项目中遇到一个求两个任意 多边形 重叠面积的问题，乍一想感觉问题太简单了；然后就出现了下图的尴尬情况：这玩意不好求啊，网上搜索找到一个方案采用了Sutherland-Hodgeman-Polygon-Clipping Algorihtm（自行了解），主要解决了凸多变形重叠区域的contour的寻找，算法的思想就是沿着一个凸 多边形 的边裁切， 直到将所有的凸 多边形 的边全部裁切完成。但是面对非凸 多边形 而且有多个闭合的相交区域的情况的时候，一条边的裁切可能会将另一条边裁掉，因此算法不适用。 题目地址：http://www.cnblogs.com/try86/archive/2012/04/22/2465416.html 这一题，若 点 在边上，也将 点 看做成 多边形 内。 对于凸 多边形 有很多种方法 判断 点 在 多边形 内，但若是 凹 多边形 ，则靠谱的方法不多，可以谷歌一下。 1）水平/垂直交叉 点 数判别法（适用于任意 多边形 包括 凹 凸边形） 注意到如果从P作水平向左的射线的话，如果P在 多边形 内部，那么这