费马的“关于此，我确信已发现了一种美妙的证法，可惜这里空白的地方太小，写不下”的原文是什么？

关于此，我确信已发现了一种美妙的证法，可惜这里空白的地方太小，写不下, x^{n}+y^{n}= z^{n} 显然是一个微分流形，关于向量的加法构成一个李群，黎曼度量g定义在 sinnx,sinny,sinnz , Hilbert 定理有 R^{3} 中不存在具有常负高斯曲率的完备曲面， Lobatchevski 上半平面高斯曲率 K\equiv-1 ,令 H\subset R^{2} ,不存在 H 在欧氏空间 R^{3} 中的等距浸入，一个自然的问题是， Lobatchevski 上半平面 H 是否可以等距嵌入(浸入)到较高维数（ n\geq4 ）的欧氏空间之中？定理（ Rosenborn ） Lobatchevski 上半平面 H 可以等距浸入到欧氏空间 R^{5} 中，等距浸入不等于有整数解，且不排除当 x,y,z,n 充分大时有整数解的可能性，n维向量场， \omega_{a}=x^{n},\omega_{b}=y^{n},\omega_{c}=z^{n}, \omega_{a},\omega_{b},\omega_{c} 的测地线 cosnx\leq1,cosny\leq1,cosnz\leq1,
x^{n}+y^{n}=z^{n} 等价于 cosnx+cosny=cosnz ,——它有显而易见的整数解：

x^{n}+y^{n}=z^{n} ，n不变的x,y,z向量场的加法运算，费马大定理有x=0,y=0,z=0成立，加法定义测度的空间填充，费马大定理不成为定理，我们定义 \mathbb{N}^k 是自然数的 k 次幂构成的集合，即 \mathbb{N}^k=\{n^k\mid n\in\mathbb{N}\} 。那费马大定理就等价于： \mathbb{N}^k 对于 k\geq3 是无和集，

n维空间填充定理：1.一维线

\Omega_{A} ，测地线直线数轴

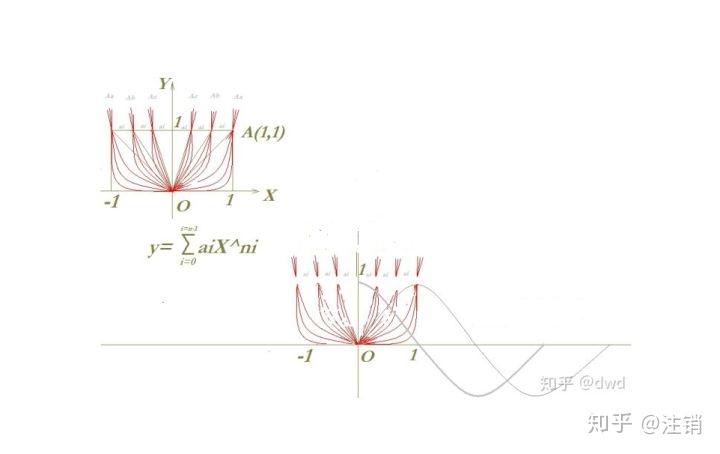
二维面 \Omega _{B}=\sum_{i=0}^{2}{a_{i}}x^{n-i} ,三维体 \Omega_{C}=\sum_{i=0}^{3}a_{i}x^{n-i} ,四维空间 \Omega_{D}=\sum_{i=0}^{4}a_{i}x^{n-i} ......,n维空间 \Omega_{N}=\sum_{i=0}^{n}{a_{i}}x^{n-i} ......,

被完全填充：填充

\gamma 一定垂直于被填充 \Omega ，势能最小， \gamma 是 \Omega 的测地线（证明从略）

n维空间完全填充的定义：非0填充γ一定垂直于被填充Ω，γ是Ω的测地线时成为完全填充（填充密度最大）

2.

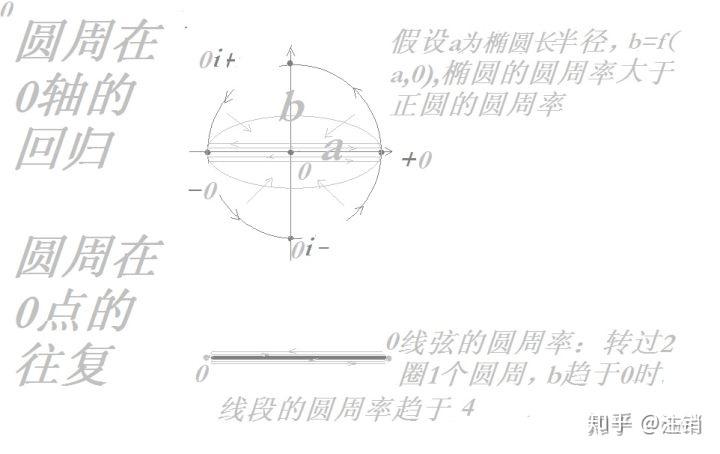
\Omega^{n} 的测地线是 f(t)=f(a_{i}cos\omega _{i}x,b_{i}sin\omega_{i}x) ,平行线是 f(t)=f(a_{i}sin\omega_{i}x,b_{i}cos\omega_{i}x) （证明从略），数学上， x=sinx,x=cosx 同解。

3.0点填充可100%填充.

4.公式推广到n维空间，不同的维度数有不同的填充频率

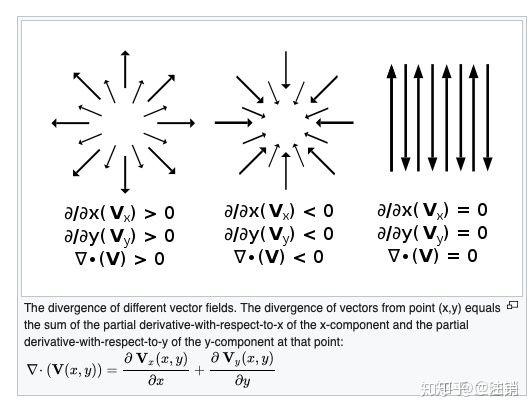
假设空间中有向量场 \mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k} ，那么观察空间中的微小的长方体：

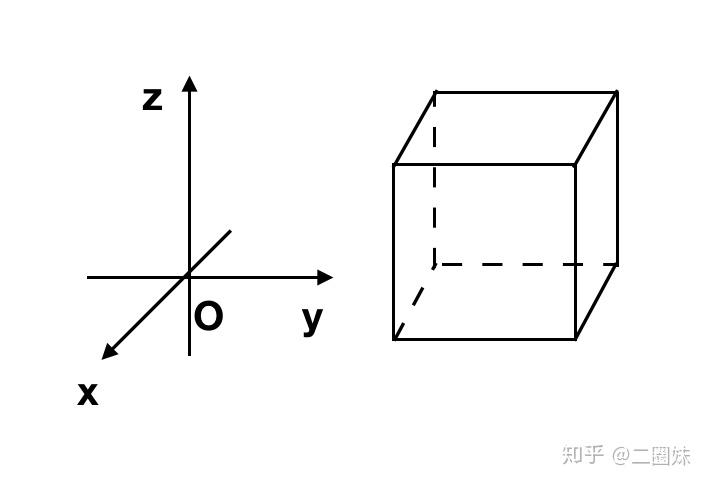
散度:

\mathbf{div\,} \mathbf {F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} \\

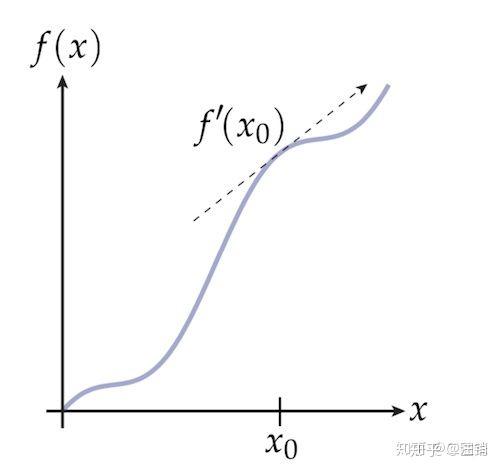
散度是给我们一个向量场，我们得到的是一个标量，

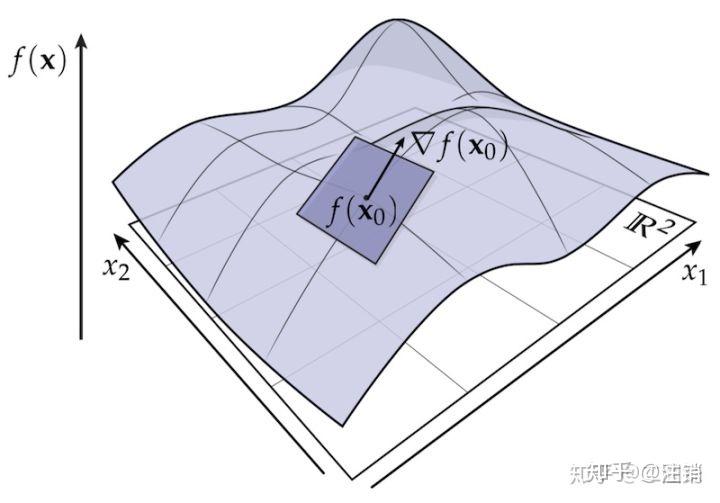
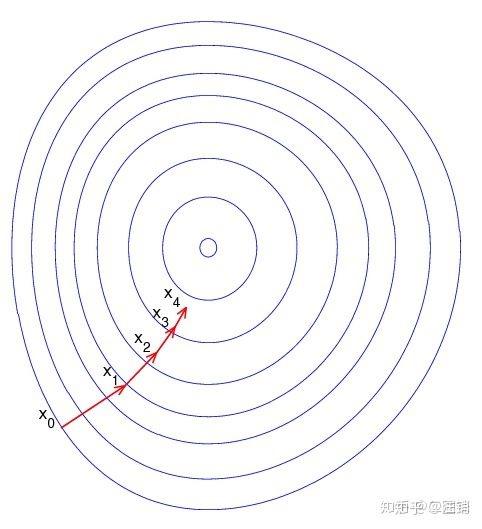
加法群性质定理，三个正交加法群一定形成环，

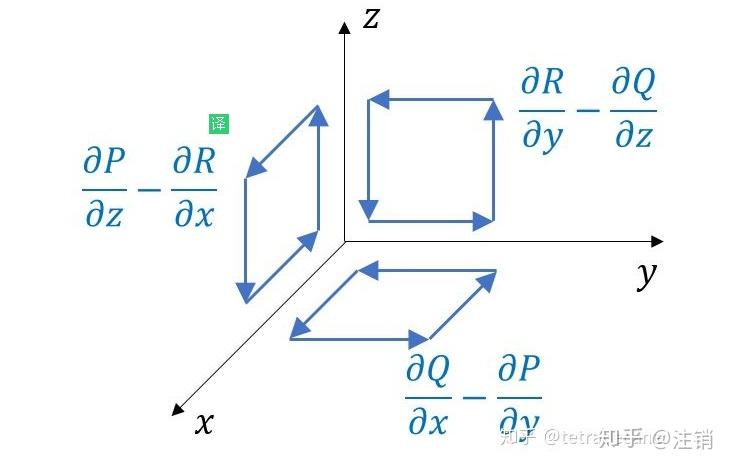
n≥3, x^{n},y^{n},z^{n} 形成环，不是群，

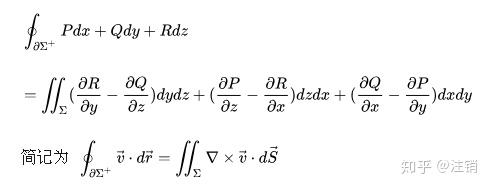
考虑二维的情况，

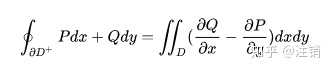
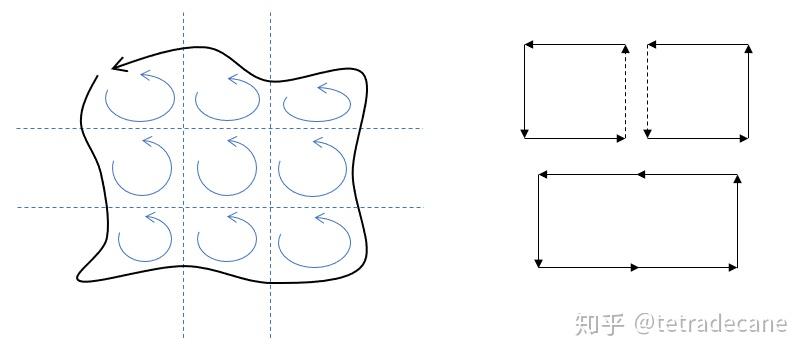
我们定义 \mathbb{N}^k 是自然数的 k 次幂构成的集合，即 \mathbb{N}^k=\{n^k\mid n\in\mathbb{N}\} 。那费马大定理就等价于： \mathbb{N}^k 对于 k\geq3 是无和集 。

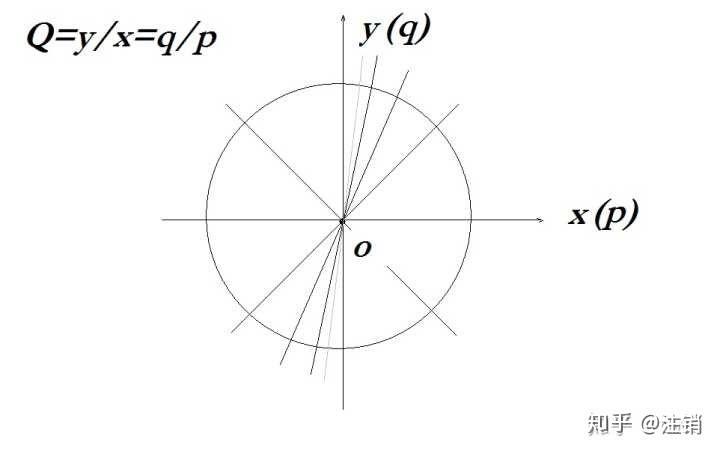
对于任意无理数 \alpha ， n\alpha-[n\alpha] 在 [0,1] 中稠密，自然数映射到 \left[ 0，1 \right] 区间，任一无理数等于两有理数的和（差）、和差表示：实数的1+1定理。