时隔两年,我终于运行出了这两行Mathematica代码
起因
那是两年前,我在知乎上看到了这样一个回答:
这里面提到了这样一行代码:
Trace[Integrate[Sin[x]^n,{x,0,Pi/2}],TraceInternal->True]按照作者 @酱紫君 的说法,这段代码在某种程度上就可以显示出Mathematica计算积分的过程。谁能想到,这短短的一行代码(我后来又在上面加了另一行)成为了萦绕在我心头两年的一个心结:我在我能找到的 任何一台计算机 上都运行不出这两行代码的结果。
下面是这两行代码:
$OutputSizeLimit = Infinity;
Trace[Integrate[Sin[x]^n, {x, 0, Pi/2}], TraceInternal -> True]背景介绍
数学专业和理论物理专业的同学肯定对Mathematica这个软件并不陌生,简单点讲,可以把它当成符号计算的计算器。
我们都知道什么是数值计算,比如说,当我们拿来一个普通的计算器,按下1+1之后,计算器会输出2。又比如说拿到了一个高级计算器(你的手机上很可能也有这个功能),按下sqrt(2)之后,得到的结果是1.414,这样计算器就帮你计算出了根号二的取值,这些都是数值计算。
在数学和理论物理的某些领域的研究中,符号计算更为常见。所谓符号计算,就是"推导数学公式"。比如,下面这个展开就是符号计算:
(a+b)(c+d)=ac+ad+bc+bd
又比如说,求解下边这个一元二次方程:
x^2+x+3=0
得到了下边这样一个结果:
x_1=\frac12(-1+i\sqrt{11}),x_2=\frac12(-1-i\sqrt{11})
这也是符号计算。
Mathematica是个数学软件,它可以进行符号计算,换句话说,只要输入适当的指令进入这个软件,它就可以自己推导公式。比如上边两个符号计算的例子可以用这样的指令来完成:
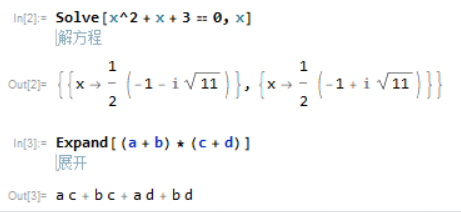
这样就将数学家和理论物理学家从繁重的劳动中解放了出来。可以这样设想,在有了普通计算器之后,会计们再也不用敲算盘了。同理,有了这个软件之后,数学家和理论物理学家们至少有相当多的繁重推导可以用计算机来完成了。
一个显而易见的问题是,符号计算极其困难。学过数学的人都知道,数学公式的推导凝结了人类的智慧。让计算机也做到这一点,真的是难于上青天。
我举一个高等数学中的例子:计算积分(这也是文章最开始提到的那个问题)。如果学过高等数学的话就会清楚,计算积分是一种技巧性极强的工作,需要深厚的数学底蕴和丰富的经验。最重要的一点是,几乎所有的函数都是 积不出来的 。一个很简单的原因就是,对于一个简单的函数,其积分经常会及其复杂。比如:
\int \sqrt{x^2+a^2}dx=\frac12x\sqrt{x^2+a^2}+\frac12a^2\ln(x+\sqrt{x^2+a^2})+C
一件很神奇的事情是,Mathematica这个数学软件计算积分的能力极其强大,甚至于在速度准度和广度上远超人类。可以说,除了极少数专精于微积分以及复分析、特殊函数论的人(我们称他们为“积佬”)以外,Mathematica积不出来的函数,你也很可能积不出来。下面是一个专精于积分的专栏,里面有一群积佬:
对于积分 \int^b_a f(x)dx 来说,在Mathematica中输入这样一行代码就可以将它计算出来:
Integrate[f[x],{x,a,b}]比如对于上边那个巨复杂的例子来说,这样就可以轻松解决:

既然它这么好用,那么可不可以看一下它的计算过程呢?于是就有了文章开头的那个问题:
解答
酱紫君引用了Mathematica帮助文档的一段话:
在手工计算中,符号积分通过大量的涉及变量替换等的技巧来进行.
但在 Wolfram 语言中,符号积分由相当少的非常系统化的程序来进行. 对于不定积分,这些程序的思想是找出积分的最一般形式,然后对其微分求出待定系数.
这个程序常常在中间阶段产生大量复杂的代数表达式,有时是非常复杂类型的数学函数. 但这个程序的优点是它是完全系统化的,其运算不需要只有人类才能提供的智慧.
Wolfram 语言中的大多数算法,包括所有特殊的情况,都是人为构建的. 但一些算法由计算机自动地创建. 使用在 Wolfram 语言中的大多数这种公式实际上由 Wolfram 语言自己导出. 导出公式的运算常常需要几个月的时间,但结果是能以最优的方式进行计算.
这段话已经说得相当明白了。酱紫君接着说,如果你真的想看看Mathematica的“计算过程”,可以输入这样一段代码:
Trace[Integrate[Sin[x]^n,{x,0,Pi/2}],TraceInternal->True]这样它就可以告诉你 \int_0^\frac\pi2 \sin^n xdx 这个积分的计算过程。
这个积分咋一看还是可以在人力的极限之下完成的。只需要注意到:
\int^{\frac{\pi}{2}}_{0}dx=\frac{\pi}{2}
\int^{\frac{\pi}{2}}_{0}\sin xdx=1
\int^{\frac{\pi}{2}}_{0}\sin^{n}xdx=-\frac{\cos x\sin^{n-1}x}{n}|^{\frac{\pi}{2}}_{0}+\frac{n-1}{n}\int^{\frac{\pi}{2}}_{0}\sin^{n-2}xdx=\frac{n-1}{n}\int^{\frac{\pi}{2}}_{0}\sin^{n-2}xdx
立刻就可以得到:
\int^{\frac{\pi}{2}}_{0}\sin^{n}xdx=\left\{ \begin{aligned} &\frac{(n-1)!!}{n!!} \frac\pi2 &\text{n even}\\ &\frac{(n-1)!!}{n!!}&\text{n odd} \end{aligned} \right.
这个式子称为“华莱士公式”。
但是,我们还是把这个问题想得太简单了。从来也没有人说过,n一定要是个整数。比如,如果 n=\frac12 ,那么被积函数就是 \sqrt{\sin x} 。这绝对是一个令人望而生畏的积分。更进一步,如果n是个无理数呢?n是个复数呢?一个非实数的幂次本身就是一个非平凡的东西。你能说出x的1+i次幂代表着什么吗?
所幸我们还可以猜测一下,可以把上边的华莱士公式写成Gamma函数的形式:
\int^{\frac{\pi}{2}}_{0}\sin^{n}xdx=\frac{\sqrt{\pi}}{2}\frac{\Gamma(\frac{1+n}2)}{\Gamma(1+\frac{n}2)}
我们证明了这个式子对于整数n是成立的。对于非整数n是这样吗?这是不好证明的,不过我们可以把它丢进Mathematica中看看。结果证明了我们的猜想:

现在,我们只需要运行这一行代码就可以得到Mathematica中的计算过程了:
Trace[Integrate[Sin[x]^n,{x,0,Pi/2}],TraceInternal->True]运行
输出的结果极其庞大,这是不难想象的:在Mathematica中调用的函数,一定会非常复杂,而这些复杂的函数又调用别的函数。把它们全都写出来,一定是一个极其复杂的过程。为了把这些结果全输出出来,我又加了一行,这就变成了两行代码:
$OutputSizeLimit = Infinity;
Trace[Integrate[Sin[x]^n, {x, 0, Pi/2}], TraceInternal -> True]手头有Mathematica的朋友可以去试试,你们的电脑大概率会当场去世。事实就是,我找到了我所能找到的几乎所有电脑,无一例外全部卡死,在那里放个几天几夜也不会输出任何结果。
这让我开始不禁怀疑:这个程序真的能够运行出结果吗?会不会是Mathematica的bug?这难道就是传说中的停机问题:它是运行时间太长,还是根本就停不下来?
就这样度过了两年时光,期间我找了数位物理系的老师,请他们运行这一段代码,最终都是无功而返。甚至有的老师还在怀疑:你这代码是用来搞破坏的吧?
最终我狠了狠心,找到了一位做计算光学的教授,说明了来意。教授欣然将他的工作站借给我用了一晚上。这台工作站有着恐怖的 128G内存, 其他指标诸如CPU和显卡等等也是当时最顶级的配置。
我把程序输入计算机中,开始了漫长的等待。在鏖战了3个小时之后(期间还跳出过各种弹窗和未响应),终于输出了程序的结果。望着满屏的乱码,我的眼睛里都快冒出小星星了。
输出的结果足足有512MB。这是个什么概念?假设用ASCII编码,一个字母占用一个字节,那么输出就是536870912个字符,也就是5亿字符。假设一张纸上可以写1000个字符,那么这些字符可以写满五十万张纸,可以叠五十米高。

当然,后面酱紫君还说:
讲道理过程有什么用啊, 思路才是真正重要啊, TraceInternal 里的过程你看了吗, 你看出啥了吗......
Sin[x]^n 的积分在四分之一时间内约化到了一个超几何函数, 然后可能是撞到奇点还不知啥, 绕了半天才化简出一个阶乘函数...
你难道也往作业上写个超几何函数吗...老师会认识吗...
也不知道他是怎么看出来“Sin[x]^n 的积分在四分之一时间内约化到了一个超几何函数”的,这大约就是真大佬吧……
结果
说了这么半天,这程序跑出来的到底是什么啊?完整的截下来已经是不可能的了,毕竟这东西是用滚轮划半个小时划不到头的。只好随便截几张让大家饱饱眼福了……



最后,想看完整版的可以找我。只不过这个运行结果拿到你电脑上,也大概率是打不开的……
就酱。
