|
|
相关文章推荐
|
旅行中的啄木鸟 · 优化改进YOLOv5算法：加入ODConv+ ...· 2 月前 · |
|
|
魁梧的绿茶 · 西部文艺研究投稿_专门发布期刊官方征稿信息_ ...· 5 月前 · |
|
|
活泼的金针菇 · pg.lost Tour ...· 5 月前 · |
|
|
俊逸的肉夹馍 · 人口第一大县易主！江西100个县级行政区人口 ...· 1 年前 · |
|
|
有情有义的蟠桃 · python loompy - CSDN文库· 1 年前 · |
|
|
气宇轩昂的蜡烛 · 《查理曼大帝密码》：典型的华丽探险大片_影音 ...· 1 年前 · |
我正在尝试实现一种算法，当点被拖动时，该算法将对齐椭圆上的矩形。
我掌握的数据如下：
- 我知道哪个角落被拖着
- 它的起始位置
- 它的结尾位置
我以前的算法是对齐相邻的角，但只有当椭圆或矩形不成角时才能对齐。
我正在尝试实现一些像Figma所做的事情：
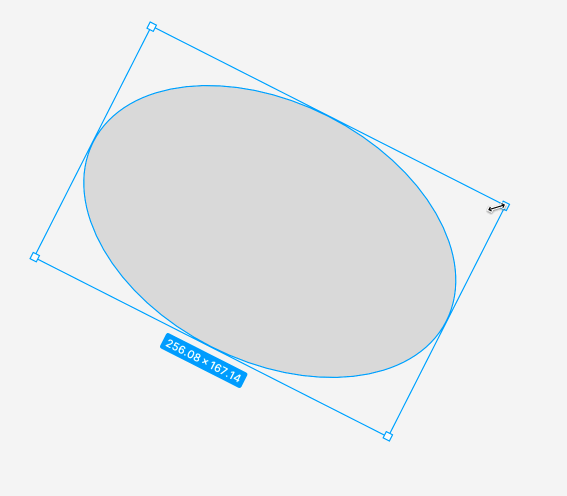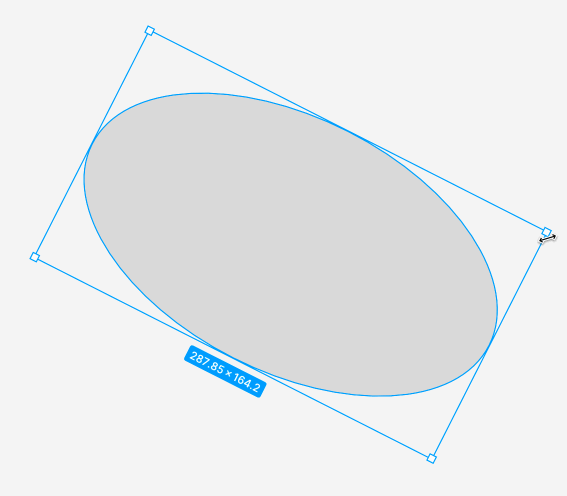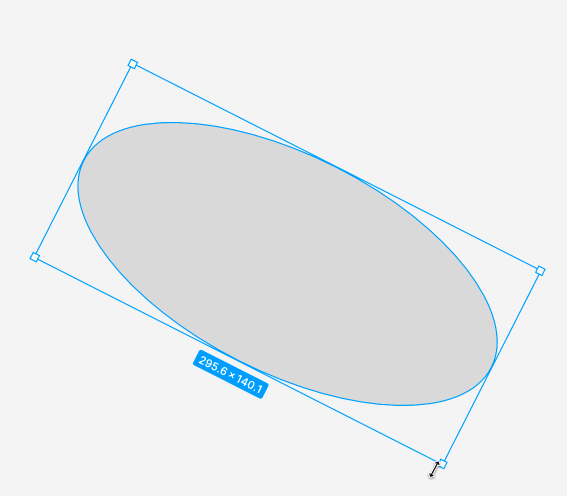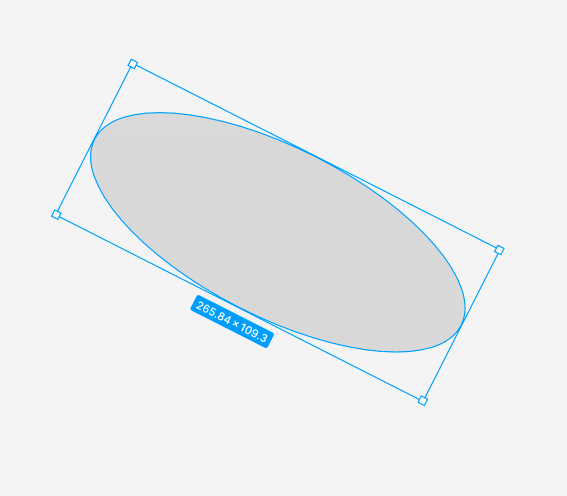
我目前的想法是把那些在拖动时被改变的边和其他没有改变的边匹配到改变的边的大小。但我不确定这是否正确。
1 个回答
高票数
最新
MBo
修改于2022-12-02 18:07
得票数
1
用中心点
(CX, CY)
和两个单位方向向量
(WX, WY)
和
(HX, HY)
描述矩形，
W
是半宽的，
H
是半高的。
据我所知，矩形斜率是保留的，所以方向向量保持不变。
当角号
k
被移动时，它的新位置是
(NX, NY)
。相反的顶点有数字
(k+2)%4
，它的位置是
(PX, PY)
(不变)
新中心
CX' = (PX + NX) / 2
CY' = (PY + NY) / 2新半宽半高
W' = 0.5 * Abs(WX * (NX - PX) + WY * (NY - PY))
H' = 0.5 * Abs(HX * (NX - PX) + HY * (NY - PY))所属 标签
algorithm
geometry
相似 问题
- 在进行数据库调用的线程中使用ruby超时 得票数 5
- 如何在Java中的某个位置替换字符串中的字符？ 得票数 1
- 整个数据集的回归线以及基于R ggplot2中的组的回归线？ 得票数 6
- 构建一个运行其他安装程序的安装程序 得票数 2
- 用于人脸和眼睛检测的最佳opencv版本 得票数 1
- 为什么我的阶乘数查找器返回在C++中输入的数字？(编辑) 得票数 0
- 为整个项目定义CSS中自定义字体的大小 得票数 2
- Socket.io仅向房间内的部分用户发送消息 得票数 1
- 我们能知道用于启动正在运行的容器的docker run命令吗？ 得票数 0
- 基于两层的对象数组排序 得票数 1
关注
腾讯云
开发者
公众号
将获得
10元无门槛代金券
洞察腾讯核心技术
剖析业界实践案例
Copyright © 2013 - 2023 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号： 粤B2-20090059 深公网安备号 44030502008569
腾讯云计算（北京）有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
扫码关注腾讯云开发者
领取腾讯云代金券
推荐文章
|
|
魁梧的绿茶 · 西部文艺研究投稿_专门发布期刊官方征稿信息_万维书刊网 5 月前 |
|
|
活泼的金针菇 · pg.lost Tour Announcements 2025 & 2026, Notifications, Dates, Concerts & Tickets – Songkick 5 月前 |
|
|
有情有义的蟠桃 · python loompy - CSDN文库 1 年前 |