verilog数的表示和定点化

1.1 数制转换

十进制整数转换成其他进制数：“除基取余”：十进制整数不断除以转换进制基数，直至商为0。每除一次取一个余数，从低位排向高位。

十进制小数转换成其他进制数：乘基取整，直至ε，高位到低位；“乘基取整”：用转换进制的基数乘以小数部分，直至小数为0或达到转换精度要求的位数。每乘一次取一次整数，从最高位排到最低位。

若要转换的数既有整数又有小数时，整数、小数分别转换。

1.2 二-十进制码（BCD码）

用4位二进制编码表示十进制的0-9十个数码。对于一个多位的十进制数，需要有与十进制位数相同的几组BCD代码来表示。

1.3 ASCII码

美国标准信息交换码，采用7位二进制表示27=128个包括0-9，字母等可打印字符。

数字0-9的ASCII码范围为：011_0000-011_1001:48~57

大写字母A-Z的ASCII码范围为：100_0001-101_1010:65~90

小写字母a-z的ASCII码范围为：110_0001-111_1001:97~122

1.4 有符号数和无符号数

有符号数指的就是带有符号位的数据，其中最高位就是符号位（如果最高位为0，那么表示是正数，如果最高位为1，那么表示是负数）；无符号数就是不带有符号位的数据。

考虑一个4位的整数4’b1011：

如果它是一个无符号数据，那么它表示的值为：$ 1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+1\times 2^{0}=11$

如果它是一个有符号数，那么它表示的值为：$ -1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+1\times 2^{0}=-5$

所以相同的二进制数把它定义为有符号数和无符号数表示的数值大小有可能是不同的。有符号数和无符号数转化为10进制表示的时候唯一的区别就是最高位的权重不同，由上例知，无符号数最高位的权重是，而有符号数最高位的权重是−23 。

正因为有符号数和无符号数最高位的权重不同，所以他们所表示的数据范围也是不同的。比如，一个4位的无符号整数的数据范围为0~15，分别对应二进制4’b0000~4’b1111，而一个4位的有符号整数的数据范围为-8~7,分别对应二进制4’b1000~4’b0111.

扩展到一般情况，一个位宽为M的无符号整数的数据范围为$0\sim2^{M-1}$，而一个位宽为M的有符号整数的数据范围为$-2^{M-1}-1\sim 2^{M-1}-1$。

N位有符号正数X的补码与该正数的原码相同，如4位有符号数0011的补码还是0011，对应无符号数3.

N位负数X的补码所表示的无符号数对应$2^{N}-|X|$ ，如4位有符号数1011(-3)的补码是1101，对应无符号数$13=2^4−|−3|$.

1.4.1 有符号数

数据的量化以及截位处理中，一种比较精确的处理方式就是先对截位后的数据进行四舍五入（round），如果在四舍五入的过程中由于进位导致数据溢出，那么我们一般会对信号做饱和（saturation）处理。

饱和处理就是如果计算结果超出了要求的数据格式能存储的数据的最大值，那么就用最大值去表示这个数据，如果计算结果超出了要求的数据格式能存储的数据的最最小值，那么就用最小值去表示这个数据。

规定：如果一个有符号数的总位宽为32位（其中最高位为符号位），小数位宽为16位，那么这个有符号数的数据格式记为32Q16。依次类推，10Q8表示这个数是一个有符号数（最高位为符号位），且总位宽为10位，小数位宽为8位。16Q13表示这个数是一个有符号数（最高位为符号位），且总位宽为16位，小数位宽为13位。总而言之，如果定义一个数据为mQn（m和n均为正整数且m>n）格式，那么我们可以得到三个重要的信息:

1、mQn是一个有符号数，最高位为符号位

2、mQn数据的总位宽为m

3、mQn数据的小数位宽为n

1.4.2 有符号整数的符号位扩展

如果把一个4位的有符号整数扩展成6位的有符号整数。假设一个4位的有符号整数为4’b0101，显然由于最高位为0，所以它是一个正数，如果要把它扩展成6位，那么只需要在最前面加2个0即可，扩展之后的结果为：6’b000101。

假设一个4位的有符号整数为4’b1011，显然由于最高位为1，所以它是一个负数，如果要把它扩展成6位，，前面不是添2个0，而是添2个1，扩展之后的结果为：6’b111011。为了确保数据扩位以后没有发生错误，这里做一个简单的验证：

$4'b1011=-1*2^{3}+0*2^{2}+1*2^{1}+1*2^{0}=-8+0+2+1=-5$

$6'b111011=-1*2^{5}+1*2^{4}+1*2^{3}+0*2^{2}+1*2^{1}+1*2^{0}==32+16+8+0+2+1=-5$

显然扩位以后数据大小并未发生变化。综上：对一个有符号整数进行扩位的时候为了保证数据大小不发生变化，扩位的时候应该添加的是符号位。

1.4.3 有符号小数

接下来研究一下有符号小数。前面已经规定了有符号小数的记法。

假设一个有符号小数为4’b1011，它的数据格式为4Q2，也就是说它的小数位为2位。那么看看这个数表示的10进制数是多少

$4′b10.11=−1∗2^{1}+0∗2^{0}+1∗2^{−1}+1∗2^{−2}=−2+0+0.5+0.25=−1.25$

显然，小数的计算方法实际上和整数的计算方法是一样的，只不过我们要根据小数点的位置来确定对应的权重。

下面看看有符号小数的数据范围。拿4Q2格式的数据来说，它的数据范围为$−2∽2−2^{−2}$,对应二进制4’b1000~4’b0111.扩展到一般情况，mQn格式的数据范围为:$−2^{M−N−1}∽2^{M−N−1}+1-2^{-N}$。

最后再来看看有符号小数的数据扩展。假设一个有符号小数为4’b1011，它的数据格式为4Q2，现在要把这个数据用6Q3格式的数据存储。显然需要把整数部分和小数部分分别扩一位，整数部分采用上一节提到的符号位扩展，小数部分则在最后面添一个0，扩展以后的结果为6’b110110，接下来仍然做一个验证：

$4′b10.11=−1∗2^{1}+0∗2^{0}+1∗2^{−1}+1∗2^{−2}=−2+0+0.5+0.25=−1.25$

$6'b110.110=-1*2^{2}+1*2^{1}+0*2^{0}+1*2^{-1}+1*2-{2}+0*2^{-3}$

$=-4+2+0+0.5+0.25+0=-1.25$

显然，扩位以后数据大小并未发生变化。

总结：有符号小数进行扩位时整数部分进行符号位扩展，小数部分在末尾添0.

1.4.4 两个有符号数的和

两个有符号数相加，为了保证和不溢出，首先应该把两个数据进行扩展使小数点对齐，然后把扩展后的数据继续进行一位的符号位扩展，这样相加的结果才能保证不溢出。

现在把5Q2的数据5’b100.01和4Q3的数据4’b1.011相加。

Step1、由于5Q2的数据小数位只有2位，而4Q3的数据小数点有3位，所以先把5Q2的数据5’b100.01扩位为6Q3的数据6’b100.010，使它和4Q3数据的小数点对齐

Step2、小数点对齐以后，然后把4Q3的数据4’b1.011进行符号位扩展成6Q3的数据6’b111.011

Step3、两个6Q3的数据相加，为了保证和不溢出，和应该用7Q3的数据来存储。所以需要先把两个6Q3的数据进行符号位扩展成7Q3的数据，然后相加，这样才能保证计算结果是完全正确的。

以上就是两个有符号数据相加需要做的一系列转化。下面思考为什么两个6Q3的数据相加必须用7Q3的数据才能准确的存储他们的和。因为6Q3格式数据的数据范围为$-4\sim 4-2^{-3}$ ;那么两个6Q3格式的数据相加和的范围为$-8\sim 8-2^{-2}$；显然如果和仍然用6Q3来存一定会溢出，而7Q3格式数据的数据范围为$-8\sim 8-2^{-3}$ ，因此用7Q3格式的数据来存2个6Q3格式数据的和一定不会溢出。

结论：在用Verilog做加法运算时，两个加数一定要对齐小数点并做符号位扩展以后相加，和才能保证不溢出。

1.4.5 两个有符号数的积

两个有符号数相乘，为了保证积不溢出，积的总数据位宽为两个有符号数的总位宽之和，积的小数数据位宽为两个有符号数的小数位宽之和。简单来说，两个4Q2数据相乘，要想保证积不溢出，积应该用8Q4格式来存。这是因为4Q2格式数据的范围为：$-2\sim 2-2^{-2}$，那么两个4Q2数据相乘积的范围为：$-4+2^{-1} \sim 4$，而8Q4格式的数据范围为：$-8\sim 8-2^{-4}$，一定能准确的存放两个4Q2格式数据的积。

结论: mQn和aQb数据相乘，积应该用(m+a)Q(n+b)格式的数据进行存储。

1.4.6 有符号数乘法

例如有符号数[3:0]a * [3:0]b. 其中a=-5，b=7。a用补码表示为1011，b用补码表示是0111,对于这个例子，乘法过程如下：

其中，b的符号位跟a相乘的时候需要注意，如果b的符号位是1，则b的符号位与a相乘的时候实际表示的是-1*a,所以需要将a的结果按位取反加一取反加一。上面的例子b的符号位是0，所以结果是1101_1101,补码是1100011 = -35。如果遇到符号位是1的情况，比如上面的右图a=-5,b=-3，可以看到上面最后一行的结果需要对a进行取反加一取反加一才正确,并且此时取反加一也包括a的符号位。

另外，还需要注意的是所有部分积都要补符号位补到乘法输出值的位数。

其实乘法器就是由加法组成，所以b中的每一位跟a做乘法（异或）之后把部分积累加时，仍然需要遵从加法的原则，扩展符号位直到达到输出位宽，然后再加。

所以有符号乘法跟无符号乘法的区别就在这，无符号乘法不需要考虑符号位扩展问题，而有符号乘法在累加部分积的时候需要做符号位扩展，并且还要考虑符号位参与乘法时的含义不同，也就是说符号位的0表示0，但1却表示-1，所以符号位的1做乘法就不是异或而是对所有位取反再加一了。

在verilog中，一般有符号乘法器的做法是先将补码输入都转成原码，再将符号位单独拿出来进行异或，然后其余部分当作无符号数乘起来，最后再对结果取补码转回原码结果。

1.4.7 Verilog-2001有符号运算

在Verilog-1995中，integer数据类型为有符号类型，而reg和wire类型为无符号类型。而且integer大小固定，即为32位数据。在Verilog-2001中对符号运算进行了如下扩展。
Reg和wire变量可以定义为有符号类型：

reg signed [63:0] data;
wire signed [7:0] vector;
input signed [31:0] a;
function signed [128:0] alu;

函数返回类型可以定义为有符号类型。
带有基数的整数也可以定义为有符号数，在基数符号前加入s符号。

16'hC501 //an unsigned 16-bit hex value
16'shC501 //a signed 16-bit hex value

操作数可以在无符号和有符号之间转变。通过系统函数signed和unsigned实现。

reg [63:0] a; //unsigned data type
always @(a) begin
    result1 = a / 2; //unsigned arithmetic
    result2 = $signed(a) / 2;//signed arithmetic
1.4.8 注意事项
当想要进行有符号乘法时，我们想通过定义成signed让综合器选择有符号乘法器，此时我们需要把乘法器的两个输入和一个输出都定义成signed，哪怕是一个定义成signed，另一个用补码但未定义signed也不行。也可以把input port定义成signed。
1.4.9 数据传递
将一个数或者计算结果A(有符号数或者无符号)赋值给另一个数B时，根据位宽不同有以下三种情况：
当A和B位宽相同的时候的直接赋值：
无论B是有符号或者无符号结果，只是简单的将A各个二进制位上的0或者1完全不变的赋值给B对应的位，并不会传递这个数是整数还是负数，是补码还是原码。如果定义了B为signed ，则将A的各个数据位传递给B，但是在赋值给B后，这个数据按照补码存储，符号位为1为负数，否则为正数，但如果未定义signed，则默认按照无符号数值结果存储。
对于长位宽直接赋值给短位宽即A的位宽大于B的位宽的A赋值于B的情况：
无论左操作数B、右操作数A是有符号数还是无符号数，都是直接截断高位。而左操作数B二进制所表示的实际十进制数据要看左操作数B是无符号数还是有符号数，如果左操作数是无符号数unsigned，还是将A的各个低数据位传递给B，对于B来说，直接转换成十进制即可，而如果B是有符号数，则将该数据看成2的补码转换成十进制数，对应B的值。
对于短位宽赋值给长位宽的情况，需要对高位进行位扩展，具体是扩展1还是扩展0，记住：完全依据右操作数A，具体如下：
1）右操作数是无符号数，则无论左操作数是什么类型，高位都扩展成0；
2）右操作数是有符号数，则要看右操作数的符号位，按照右操作数的符号位扩展，符号位是1就扩展1，是0就扩展0；
3）上述位扩展后的结果，赋值给左操作数，按照左操作数是无符号数还是有符号数解释成对应的十进制数值，如果是无符号数，则直接转换成十进制数值，如果是有符号数，则看成2的补码转换成十进制数；
4）从上面4种情况看出，有符号数赋值成无符号数会出现数据错误的情况，因此要避免这种赋值，而其他情况都是可以保证数据正确的。
1.5 浮点表示
定点运算有两个缺点:①可处理动态范围小;②由截尾舍入产生的百分比误差随着数的绝对值的减小而增加，这个问题可利用浮点数来解决。根据IEE754-1985标准，非负数n可以用两个参数表示，即尾数M和指数E，其表示形式为：$\eta =M×2^{E}$
指数 exponent的位宽决定了可以表示数据的范围，尾数的位宽决定了可以表示数据的精度
假设:浮点数整体位宽是14bits,指数 exponent位宽5bits,尾数Significand位宽8bits.
用14bit的浮点表示十进制数32:$32=1.0∗2^{5}=0.1∗2^{6}$，(0.1为2进制表示的0.1).
所以指数exponent=110，尾数1000_0000,符号位sign=0，所以32=0_00110_1000_0000,
这种表示方法的另一个问题是由于 exponent没有符号位,没法表示负指数(比如 )
为了解决编码浪费空间问题,可以规定significand的第一位必须是1,这一过程称作归一化( normalization),所有 significands以0.1xxxxx形式表示,例如$4.5=100.1∗2^0=0.1001∗2^3$
从而使得尾数M限制为在[0.5，1]范围内的二进制小数, significand的第一位必须是1.
为了使 exponents可以表示负指数,采用 biased exponent方法。
令偏置数据( bias number)是一个根据 exponent位宽而定的居中的数（5位表示最大为25 ,居中的数是16=24 ），负指数加上这个偏置数据后可以变为正数表达。从而得到指数E，为一个正的或负的二进制整数。
$0.0625(10)=1.0∗2−4=0.1∗2−3, bias exponent=16$,故在-3指数上加16,得到新的指数13(10)=01101(2)
0.0625(10)=0_01101_10000000
-26.625(10): $26.625(10)=11010.101(2)=0.11010101∗2^5$ ,在指数5上加 bias number16,得到最终指数项21(10)=10101(2)  -26.625(10)=1_10101_11010101
1.5.1 IEEE浮点数标准
在IEEE标准中，significant的表示方法是：1.xxx….，例如$4.5=0.1001∗2^3$ ，在IEEE标准中就应该表示为$1.001∗2^2$ ，尾数的第一位1是隐含的，也就是说这个1不会出现在significant编码域，故significant编码中只包含001.
单精度浮点位宽32bit，其中指数E部分具有8位 (bias127)，尾数部分则具有23位，还有一位用做符号位S（0正，1负）。
指数部分有偏编码为E-127。E的范围为:-126~127, $2^{128}=3.4×10^{38}$;
双精度浮点位宽64bit，其中指数E部分具有11位(bias1023)，尾数部分则具有52位，还有一位用做符号位S（0正，1负）。
尾数域的最高有效位总是1，由此，该标准约定这一位不予存储，而是认为隐藏在小数点的左边，因此，尾数域所表示的值是1.M（实际存储的是M）
双精度浮点位宽64bit，其中指数E部分具有11位(bias1023)，尾数部分则具有52位，还有一位用做符号位S（0正，1负）。
尾数域的最高有效位总是1，由此，该标准约定这一位不予存储，而是认为隐藏在小数点的左边，因此，尾数域所表示的值是1.M（实际存储的是M）
$−3.75=−11.11(2)=−1.111∗2^1 ,bias127,exponent=1+127=128$, 尾数的第一位1是隐藏的，
 1_1000_0000_.1110_0000_0000_0000_0000_000
单精度浮点尾数位宽：23+1(hidden)，尾数范围：[1,$2−2^{−23}$]最大为尾数全1的情况：1+2^{−1}+…+2^{−23}=2−2^{−23},最小为尾数全0的情况：1
指数位宽：8bit，指数偏置127，e+bias∈[1,254]，e∈[-126,127]
所以正数范围中，单精度浮点最大数表示为：$2^{127}∗(2−2^{−23})≈2^{128}$; ，最小数： $2^{−126}∗1≈2^{−126}$;
1.5.2 特殊值
1.5.3 浮点加法
两个浮点数的相加：统一指数exponent对阶，先将较小的一个数的尾数右移几位，直到两个数的指数相同，然后再将尾数significant相加，最后归一化结果。
如$1001+10=1.001∗2^3+1.0∗2^1=1.001∗2^3+0.010∗2^3=1.011∗2^3$
运算过程:
(1) 首先比较阶码大小是否相等，并完成对阶: 原则是小阶向大阶看齐,即小阶的尾数向右移,相当于小数点左移,每右移一位,其指数加1,直到两数的指数相等为止。
(2) 尾数求和运算:其方法与定点加减法运算完全一样，需要把数据转换成补码形式后再进行加减法。最后结果规格化，尾数每左移一位，指数减1，每右移一位，指数加1.，转化为$1.f∗2^e$的格式
1.5.4 浮点数的乘法
浮点数的乘法运算是:尾数相乘，指数相加。乘、 除法运算步骤:
1.操作数检查；
2.阶码加操作；
3.尾数乘操作；
4.结果规格化及舍入处理。
5.浮点数的溢出判断
1.6 四舍五入（round）
　前面讲的都是对数据进行扩位，这一节说的是对数据截位时如何进行四舍五入以提高截位后数据的精度。
假设一个9Q6格式的数据为：9’b011.101101，现在只想保留3位小数位，显然必须把最后三位小数位截掉，但是不能直接把数据截成6’b011.101，这样是不精确的，工程上一般也不允许这么做.
首先举例整理思路：
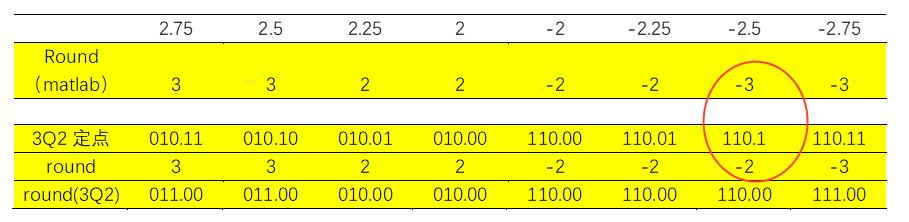可以这么理解：正数向下取整，负数向上取整。对于0.5这个地方处理不同。
特殊说明：取round（-2.5）为-2，实际上matlab运行的结果是round（-2.5）为-3。
通过整理真值表，发现round截位时的小数进位与三个变量均相关：数据符号位、小数位的最高bit，以及小数位除最高bit外的所有bit是否均为0（按位或）

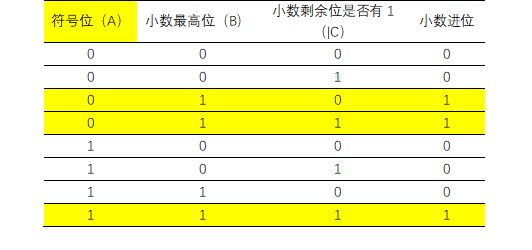
小数进位可以表示=A ? B &（|C）： B;
设输入数据din位宽为DW位，其中小数部分位宽为RD位，且需要四舍五入截掉小数部分，结果为dout。
input [DW-1:0]din; output [DW-RD:0]dout;
即carry_bit=din[DW-1]？（ din[RD-1] & (|din[RD-2:0]) ）:din[RD-1]
再考虑溢出保护：

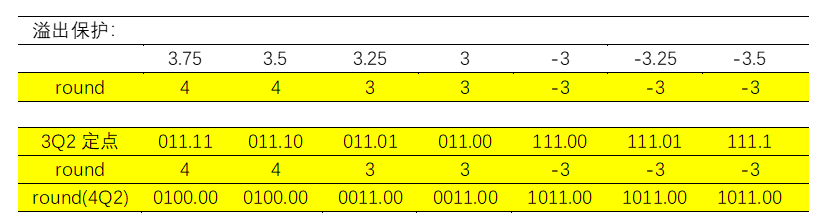
dout={din[DW-1],din[DW-1:RD]}+{ {(DW-RD){1'B0}}, carry_bit};
假设溢出不保护：

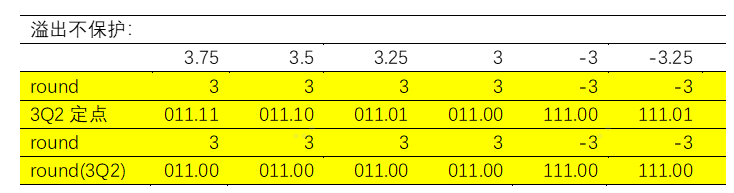
这种处理和floor几乎一摸一样，会导致频域上出现不必要的直流分量，相当于所有分量向下做了减法。
正确的做法是先看这个数据是正数还是负数，因为9’b011.101101的最高位为0，所以它是一个正数，然后再看截掉部分（此例中截掉部分是最末尾的101）的最高位是0还是1，在数据是正数的情况下，如果截掉部分的最高位为1，那么是需要产生进位的，所以，最终9’b011.101101应该被截成6’b011.110.
　如果是负数则正好相反。假设一个9Q6格式的数据为：9’b100.101101，由于最高位是1，所以这个数是一个负数，然后再看截断部分的最高位以及除最高位的其他位是否有1，此例中截断部分（截断部分为末尾的101）的最高位为1，而且除最高位以外的其他位也有为1的情况，由于负数最高位的权重是（- ），所以对于这种情况是不需要进位的，与正数不同的是，负数不进位是需要加1的。因此最终9’b100.101101应该被截成6’b100.110。
　　假设a是一个9Q6格式的数据，要求把小数位截成3位。下面是Verilog代码：
　　　　assign carry_bit = a[8] ? ( a[2] & ( |a[1:0] ) ) : a[2] ; //正数和负数四舍五入截断
　　　　assign a_round = {a[8], a[8:3]} + carry_bit ;
　　上面的代码第一行是通过判断符号位a[8]和截断部分数据特征来确定是否需要进位，如果a[8]是0,计算得到的carry_bit为1，则表示是a是正数，且截断是需要进位；如果a[8]是1,计算得到的carry_bit为1，则表示是a是负数，且截断是不需要进位的，负数不进位需要加1。代码第二行为了保证进位后数据不溢出，所以扩展了一位符号位。
1.7 饱和（saturation）截位
　所谓饱和处理就是如果计算结果超出了要求的数据格式能存储的数据的最大值，那么就用最大值去表示这个数据，如果计算结果超出了要求的数据格式能存储的数据的最最小值，那么就用最小值去表示这个数据。
例1：有一个6Q3的数据为6’b011.111,现在要求用4Q2格式的数据去存储它，显然6’b011.111转化为10进制如下：
　　$6′b011.111=1∗2^1+1∗2^0+1∗2^{−1}+1∗2^{−2}+1∗2^{−3}=3.875$
　　而4Q2格式的数据能表示的数据的最大值为4’b01.11，转化为10进制为1.75，因此4Q2格式的数据根本无法准确的存放3.875这个数据，这样就是所谓的饱和情况。在这种情况下，饱和处理就是把超过了1.75的所有数据全部用1.75来表示，也就是说，6Q3的数据为6’b011.111如果非要用4Q2格式的数据来存储的话，在进行饱和处理的情况下最终的存储结果为：4’b01.11。
　　例2：有一个6Q3的数据为6’b100.111,现在要求用4Q2格式的数据去存储它，显然6’b100.111转化为10进制如下：
　　　　　$6′b100.111=−1∗2^2+0∗2^1+0∗2^0+1∗2^{−1}+1∗2^{−2}+1∗2^{−3}=−4+0.5+0.25+0.125=−3.125$
　　而4Q2格式的数据能表示的数据的最小值为4’b10.00，转化为10进制为-2，因此4Q2格式的数据根本无法准确的存放-3.125这个数据，这是另一种饱和情况。在这种情况下，饱和处理就是把小于-2的所有数据全部用-2来表示，也就是说，6Q3的数据为6’b100.111如果非要用4Q2格式的数据来存储的话，在进行饱和处理的情况下最终的存储结果为：4’b10.00。
1.8 数据溢出
这样两个有/无符号数进行加减运算时，如果运算结果超出可表示的数值范围，会发生出错，产生溢出现象。有溢出不一定有进位、有进位不一定有溢出
 有符号加法和无符号加法在运算时硬件电路是一样的，只是对结果的解读不同.
　4-bit运算时
溢出的检查方法
“最高位的进位输入”不等于“最高位的进位输出”，说明产生了溢出。
经过一个异或门，如果C₃₁和C_out 不相等，overflow被设为1，表示溢出。
溢出只能出现在两个同号数相加和两个异号数相减的情况下。通常判别溢出的方法用双高位法：
所谓双高位判别，即规定符号位（用CS表示）有进位时，CS=1，否则 CS=0。数值部分最高位（CP表示）有进位时CP=1，否则 CS=0。若CS⊕CP=1（"异或"运算），则有溢出产生。
1.9 乘累加运算
在进行带小数位数的乘累加运算时，例如滤波运算，如如果滤波器系数位18位，其中包含16位小数位，滤波器长度为16，最终计算完成想把滤波器系数的16位小数全部截断，由于滤波器长度为16，所以加法最多会向上进位4位，所以在累加运算的时候，并不需要16位小数精度的加法器，因为累加后还是要截断，其实可以在乘法运算后，先截掉一部分小数位数，剩下8位小数(4位的进位，4位其实就够了，但考虑到裕量，留8位)，在进行累加运算后，再截掉剩下的8位小数，不仅可以节省资源和功耗，也保留了数据运算的精度。
2. 数字定点化
数字设计中浮点数定点化的问题其实就是在电路中表示十进制的小数的问题。
一个浮点数用多少位的整数来表示
如(16, 2)，则表示用16位整数来表达浮点数
假设为有符号数
则其中：1位为符号位，2位数为表达整数，剩余13位表达(0, 1)的小数
取绝对值后，找到最大值，并截断取整为maxNum
分析需要多少位来存maxNum，剩余的位数则一个留给符号位，其余位留给小数位
如用32位定点存浮点数，用25位来存整数，留1位符号位，剩6位给小数，故位宽表示(32, 25)，标值为Q6
定点值 $fix=float∗2^6$，将整数左移6位，低6位则是小数转换而来
定点能表示的浮点数精度为：126=0.015625，用最小的定点数1，来转化成最小浮点数，得到精度值
2.2 定点到浮点
一句话表达：二进制转化为十进制整数，定点整数除以$2^Q$，做浮点运算，结果即为对应浮点数。
总体过程如下图：
主要步骤：
知道标值Q，则定点是浮点转换的逆过程
公式为 $float=fix*2^{-13}$
整数部分，fix右移13位后得到的结果
小数部分，就是用定点除法运算fix/2^13的余数mod，（47013%8192=6053*（1/2^13）=0.73889...）。
通常情况下，软件应该依据算法性能的指标推导出每个子算法模块需要用到的Bit_width数，但是由于分工不同，对硬件的sensor没有那么敏感，经常会造成过大的位宽定义，以及硬件接受不了的冗余设计。这里列举几点说明：
1、  通常情况下，权重weight的bit位宽为6~8之间，不建议超过此约束。
2、  数据路径上开窗的大小（3x3）或者（5x5）是非常关乎硬件资源的，决定line_buffer是否增加2行的存储深度。
3、  不建议算法设计除法运算，能用乘替换的替换掉。对于2^n次方的除法或者乘法，建议用左移或者右移来设计。
4、  不建议将中间的某个计算好的变量在后级算法中多次使用，因为硬件有时序的概念，后级需要使用的话，需要将前级的结果用fifo做delay之后再使用，损耗寄存器或者Mem。
5、  算法中的乘法操作数的位宽通常设计为20bit*20bit，不建议设计为40bit*40bit。
6、  在保证算法性能的基础之上，浮点数定点化之后的小数位的位宽能小就小，或者说整体位宽能做多小就做多小。
7、  详细的评估算法的位宽变化之后的面积数据需要综合来支撑，前期评估可以按照经验值系数来折算。
8、  算法中涉及256个32bit模板按照规则（取最大或者最小或者RR或者带权重weight取模板），软件看不到时序概念，硬件是需要分组分级来处理该事件的（指定工艺下时序不过，相当于功能bug，相当于白做），会消耗大的逻辑资源以及lantancy。
9、  软件需要有复用思维，加法器和乘法器能复用就复用，在写法上就能够做到。
3. 举例自适应滤波器系数定点化
滤波器系数更新公式：
其中NLMS步长：
利用更新后的滤波器系数进行自适应滤波：
根据滤波器系数更新公式计算得到的自适应计算的滤波器系数$\overrightarrow{h}$总是处于（-1，1）的小数范围内，为了对自适应得到的滤波器系数进行表示，在对滤波器系数进行更新的过程中，稍作修改，手动乘以2的定点化的位数(fp2-1)次方,即$&amp;amp;amp;lt;span class="math inline"&amp;amp;amp;gt;2^(fp2&minus;1)$，改为如下形式,&amp;amp;amp;lt;br&amp;amp;amp;gt;
计算自适应滤波器输出
signed 有符号运算
有符号数均为补码表示
只有计算表达式右边有无符号数，整个计算式都按照无符号数规则运算
只有算式右边全为有符号数，运算才会自动补齐所需的bit数，n+n=n+1.n*n=2n
verilog2001中用’s来特别声明有符号数，十进制的数都是有符号数
$usigned()函数在高位补0
$signed()函数会在高位补与符号位相同的bit
两个n bit数相加，得到n+1 bit结果，比如-2(3’sb110)+3(3’sb011)=1(4’sb0011)
先将被加数进行符号位扩展，再相加，结果丢掉进位。
 代码如下，
//Code Example 1: Addition - Verilog 1995
module add_signed_1995 (
input [2:0] A,
input [2:0] B,
output [3:0] Sum
assign Sum = {A[2],A} + {B[2],B};
endmodule // add_signed_1995
直接采用signed计算如下：




    

//Code Example 2: Addition - Verilog 2001
module add_signed_2001 (
input signed [2:0] A,
input signed [2:0] B,
output signed [3:0] Sum
assign Sum = A + B;
endmodule // add_signed_2001
如果是两个3bit有符号数+1bit进位。如果在verilog2001中直接用符号位拓展
sum=A+B+carry_in //整个计算式会转换成无符号计算,signed to unsigned conversion occurs
sum=A+B+$signed(carry_in) //就会出现当carry_in=1时候拓展为4'b1111，这时候本来是加1，却变成了减1
sum = A + B + $signed({1'b0,carry_in}) //正确的做法
正确的做法是
// Code Example 3: Add with Carry - Verilog 1995
module add_carry_signed_1995 ( 
input [2:0] A,dsa
input [2:0] B,
input carry_in,
output [3:0] Sum
assign Sum = {A[2],A} + {B[2],B} + carry_in; 
endmodule //add_carry_signed_1995
直接采用signed的计算方法为
// Code Example 5: Add with Carry - Correct
module add_carry_signed_final (
input signed [2:0] A,
input signed [2:0] B,
input carry_in,
output signed [3:0] Sum
assign Sum = A + B + $signed({1'b0,carry_in});
endmodule // add_carry_signed_final
signed有符号乘法
// Code Example 7: Signed Multiply - Verilog 2001
module mult_signed_2001 (
input signed [2:0] a,
input signed [2:0] b,
output signed [5:0] prod
assign prod = a*b;
endmodule
signed和unsigned 乘法
有符号a和无符号b乘法
prod = a*b; //整个运算变成无符号，-3(3'sb101)*2(3'b010)变成5(6'b000101)*2(6'b000010)=10(6'b001010)
prod = a*$signed(b); //当乘数的MSB=1的时候会出错，-2(3'sb010)*7(3'b111)变成
                     //-2(6'sb000010)*-1(6'sb111111)=2(6'sb110010)
prod = a*$signed({1'b0,b}); //正确做法
直接采用signed的计算方法为
// Code Example 11: Signed by Unsigned Multiply
module mult_signed_unsigned_2001 (
input signed [2:0] a,
input [2:0] b,
output signed [5:0] prod
assign prod = a*$signed({1'b0,b});
endmodule
signed移位
逻辑移位’>>’, ‘<<’会补零，算术移位’<<<’, ‘>>>’会补符号位
A = 8'sb10100011
A>>3; //8'b00010100 
A>>>3;  //8'b11110100
关于signed、有符号数、算数左移、算数右移、$signed()、$unsigned()的理解。
1、signed可以和reg和wire联合使用，用于定义有符号数。在代码中使用负的十进制数赋值给有符号数，在电路中是按该数值的补码形式存储的。
2、使用signed定义的类型，做加法或乘法时，对操作数扩位处理时高位补符号位；即负数补1，正数补0；不使用signed的无符号类型，高位默认补0
有符号数signed和无符号数最重要的区别就是如何扩位，无符号数是添0，有符号数时添加符号位
3、 $signed和$unsigned。首先明确这两个语句是可综合的。$signed(c)是一个function，将无符号数c转化为有符号数返回，不改变c的类型和内容。接上述代码历程：$unsigned同理。
4、算数右移>>>和逻辑右移。
对于无符号数，>>和>>>没有区别，都是按位右移，左侧补零。
有符号数的逻辑右移>>与无符号数一样，将所有位整体右移，左侧补零。
而有符号数的算数右移>>>，左侧扩位符号位，如右移n位，则左侧增加n个符号位，右侧删除n位，即进行除n运算。
 5、算数左移。同样根据（有符号数signed和无符号数最根本的区别就是如何扩位，无符号数是添0，有符号数时添加符号位） 这句话进行理解，
在移位前数据a和移位后数据b，具有相同位数情况下，不需要扩位，即整体左移n位，右侧补。此时有符号数的算数左移<<<和有符号数的逻辑左移<<效果一致。
但是在移位前数据a和移位后数据thmp，不具有相同位数情况下，a进行MSB扩位，即为1_1100_0001，然后左移1位thmp=1_1000_0010，乘2运算。
6、总结
其一：被signed定义的数据在电路中是以补码形式存储并计算的。
其二：有符号数signed和无符号数，区别在于如何扩位，无符号数是MSB添0，有符号数MSB添加符号位。
module test/**/ ;
reg signed [7:0]a,b;
wire signed [8:0]sum1;
reg signed [8:0]thmp;
reg [7:0] c,d;
wire [8:0]sum2;
initial
begin
  a = -8'd1;
  b = 8'd2;
  c = 8'b1000_0001;
  d = 8'b0000_0010;
  $display("signed a    =%b=%d",a,a);
  $display("signed b    =%b=%d",b,b);
  $display("a+b         =%b=%d",sum1,sum1);
  $display("unsigned c  =%b=%d",c,c);
  $display("unsigned d  =%b=%d",d,d);
  $display("c+d         =%b=%d",sum2,sum2);
  $display("$unsigned(a)=%b=%d",$unsigned(a),$unsigned(a));
  a=$signed(c);
  b=$signed(d);
  $display("a+b         =%b=%d",sum1,sum1);
  a=8'b1000_0010;
  b=8'b1000_0010;
  $display("a           =1000_0010=%d",a);
  $display("b           =1000_0010=%d",b);
  a=a>>2;
  b=b>>>1;
  $display("a=a>>2      =%b=%d",a,a);
  $display("b=b>>>1     =%b=%d",b,b);
  thmp=b<<<1;
  $display("thmo=b<<<1  =%b=%d",thmp,thmp);
assign sum1 = a+b;
assign sum2 = c+d;
//adder_8 u1(sum1,sum2,a,b,c,d);
initial
begin
  $vcdpluson;
signed a    =11111111=  -1
signed b    =00000010=   2
a+b         =000000001=   1
unsigned c  =10000001=129
unsigned d  =00000010=  2
c+d         =010000011=131
$unsigned(a)=11111111=255
a+b         =110000011=-125
a           =1000_0010=-126
b           =1000_0010=-126
a=a>>2      =00100000=  32
b=b>>>1     =11000001= -63
thmo=b<<<1  =110000010=-126