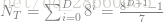高效八叉树octree：基于hash函数的数据结构_八叉树数据结构

1.基础知识

八叉树octree是一种递归、轴对齐且空间分隔的数据结构，常用于计算机几何来优化碰撞检测、最邻近搜索等，且常用于3D数据的表达。

一个八叉树结构，将有限的三维体数据等分为8个octants。octants也被称为nodes（节点，树结构概念中）或者cells（单元，空间概念中）。将空间分成等大小的立方体可以加速细分运算，且单元大小的存储也节省空间。

一个八叉树是通过递归的将空间细分成八个子单元，直到每个单元中剩余空间的大小在预定权值下，或者达到了最大树深度。每个单元都被单个轴对齐的平面细分的，类似于空间坐标系，其原点通常放在父节点的中心位置。（此处可思考不放在中心会怎么样）

因此，每个节点都可以有0或8个子节点。因此，相较于正常的网格结构，便于存储稀疏分布的结构。

2.octree的节点表达形式

传统基于指针的节点表达：

常用于octree需要频繁更新且内存消耗可以忍受的情况。通常，该节点结构体（104 byte）为：

// standard representation （104 byte）
struct OctreeNode
    OctreeNode * Children[8];//8个子节点指针
    OctreeNode * Parent; // optional 父节点指针
    Object *     Objects;//物体指针
    Vector3      Center;//中心位置vector
    Vector3      HalfSize;//octan大小vector
位于中间位置的节点以上都有，但叶节点没有子节点。因此，还常常加一项bool Isleaf; 
稍微节约一点的方式：不存储每个节点的指针，而是将8个子节点连续存储成一个块，只需要存储开头的指针就好了： 
其结构体（49 byte）： 
// block representation (49 bytes)
struct OctreeNode
    OctreeNode * Children;
    OctreeNode * Parent; // optional
    Object *     FirstObj;
    Vector3      Center;
    Vector3      HalfSize;
    bool         IsLeaf;
结合前两者：兄妹表达sibling-child 
每个节点有两个指针，一个是NextSibling，指向父节点的下一个子节点的；一个是FirstChild，指向节点的第一个子节点。 
// sibling-child representation (56 bytes)
struct OctreeNode
    OctreeNode * NextSibling;
    OctreeNode * FirstChild;
    OctreeNode * Parent; // optional
    Object *     FirstObj;
    Vector3      Center;
    Vector3      HalfSize;
简介高效的基于index索引的表达： 
现在常用的高效的octree，其节点都用基于index索引的表达，引入哈希函数的，大大节省了内存和遍历消耗。 
这种表达形式，不再存储其父节点、子节点的指针，而是在每个节点存储唯一的index索引，称为位置编码。 
而且，所有八叉树节点都存在哈希映射中，允许根据位置编码直接访问任意节点。因为，应用哈希映射，非常容易的根据任意节点的父节点和子节点来推导计算出他的位置编码。为避免不需要的哈希映射寻找不存在的子节点，节点结构西可以通过bit-mask（比特掩码，即为每个位置设置0-1编码）来确定该子节点是否被分配了内存空间。其结构体（13 byte）为： 
struct OctreeNode // 13 bytes
    Object *    Objects;
    uint32_t    LocCode;     // or 64-bit, depends on max. required tree depth
    uint8_t     ChildExists; // optional
位置编码： 
每个octant都获得了一个0-7的数字（3-bit），依赖于节点相对于其父节点中心的相对位置关系。
 
可能的编码为：左下前000，右下前001，左下后010，右下后011，左上前100，右上前101，左上后110，右上后111，如下图： 
所以，任意树中子节点的位置编码都能，通过自上而下递归的计算并连接，所有节点的octant位置编码来表达其在octree中的位置。 
为了根据位置编码来获得该节点所处树的深度，还需要设立一个标志位来表示位置编码的结束。因为，没有这种标志位，很难区分001和000001.通过使用1bit来mark序列的结束，1001可以轻松的区别于1000001，等于设立octree的根为1。1bit用于flag+每层3bit用于位置表示，所以32-bit的位置编码可以表示最大深度是10的octree。给定位置编码c，其处于树的level，深度值为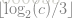 
size_t Octree::GetNodeTreeDepth(const OctreeNode *node)
    assert(node->LocCode); // at least flag bit must be set
    // for (uint32_t lc=node->LocCode, depth=0; lc!=1; lc>>=3, depth++);
    // return depth;
#if defined(__GNUC__)
    return (31-__builtin_clz(node->LocCode))/3;
#elif defined(_MSC_VER)
    long msb;
    _BitScanReverse(&msb, node->LocCode);
    return msb/3;
#endif
  按照位置编码对节点进行排序，最终顺序和cotree的遍历顺序一致，即000的会被先遍历完其子节点。这等效于morton编码(wikipedia上叫z-order curve)，它可以对多维数据线性编码，并在多level里保留数据所在位置。可以从下图中背景里的Z，知道为什么这么叫： 
给定位置编码，沿octree向上或者向下移动，两步操作实现：1.获得下一个节点的位置编码；2.在哈希映射中寻找该节点。 
为了能向上遍历octree。必须确定每个位置编码的父节点：只要去掉当前节点位置编码的最后3bit就行了： 
class Octree
public:
    OctreeNode * GetParentNode(OctreeNode *node)
        const uint32_t locCodeParent = node->LocCode>>3;
        return LookupNode(locCodeParent);
private:
    OctreeNode * LookupNode(uint32_t locCode)
        const auto iter = Nodes.find(locCode);
        return (iter == Nodes.end() ? nullptr : &(*iter));
private:
    std::unordered_map<uint32_t, OctreeNode> Nodes;
为了能向下遍历octree。必须确定每个位置编码的子节点：只要在当前节点位置编码的最后3bit加上相应的子节点位置编码就行了： 
void Octree::VisitAll(OctreeNode *node)
    for (int i=0; i<8; i++)
        if (node->ChildExists&(1<<i))
            const uint32_t locCodeChild = (node->LocCode<<3)|i;
            const auto *child = LookupNode(locCodeChild);
            VisitAll(child);
完整的octree： 
完整的八叉树，每个中间节点都有8个子节点，所有叶节点都有相同的树深度D，叶节点数 ，等于用 的分辨率细化了一个三维网格。所有节点数量为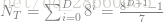 
但我们一般用octree，都不是完整的，完整的就等效于一般网格了，没必要用了。一般都是使用其对稀疏数据表达的强大能力。
                    1.基础知识八叉树octree是一种递归、轴对齐且空间分隔的数据结构，常用于计算机几何来优化碰撞检测、最邻近搜索等，且常用于3D数据的表达。一个八叉树结构，将有限的三维体数据等分为8个octants。octants也被称为nodes（节点，树结构概念中）或者cells（单元，空间概念中）。将空间分成等大小的立方体可以加速细分运算，且单元大小的存储也节省空间。一个八叉树是通过递归的将空间细分成八个子...
考虑使用SAH添加优化并进一步限制边界框
提供用于迭代刷新所有挂起的插入的选项，因为这在转换操作上可能会很昂贵
当树很大时，射线广播可能会变慢。 这似乎是由于许多对象没有被向下推入跨越八分圆边界的叶子。
 添加，更新和删除操作都会同时延迟，而对象也将被下推到树中-我们不需要两者（或两者都需要？将它们删除吗？）
 优化对象去除。
 使用类似SAH算法的方法来决定何时拆分。
 将边界缩小到最佳约束子对象的大小？
				针对光线跟踪算法计算量大和运行效率低的问题, 提出了一种采用八叉树自适应体归并(OAVM)的光线跟踪加速结构。该结构将八叉树模型的空节点自适应地聚集为包围体, 尽可能地减小了光线与空白节点的求交次数。基于OAVM的一种多级八叉树结构的特点, 提出了采用Morton码对各层级的所有节点分别进行编码的算法, 该结构所采用的存储方式和邻域查询算法有效减小了指针数量, 避免了递归搜索。同时, 该算法可以有效处理大规模动态场景的局部更新问题。基于Liang-Barsky算法, 光线相交测试的计算速度得到提升。实验结果表明, 和传统结构算法相比, 所提出算法的指针总数平均减少了54.45%, 光线相交测试时间平均缩短了52.37%, 大幅加快了相交测试速度, 提升了场景的渲染效率。
(1)三维和四维数据结构的提出。前面介绍的数据结构都是二维的，然而在有些信息系统中，需要有真三维的空间数据结构。例如矿山开采中的地下资源埋藏和采矿巷道的空间分布，如果用二维的坐标体系就根本无法很好表达。此外，矿山空间目标往往随时间不断变化着，这就提出了空间和时间信息系统的问题。
在时间信息系统中不考虑时间，是把时间看作不变的常数，即为当前的时间。而在时间和空间信息系统中，则把时间看作有过...
 import { Scene } from "three" ;
import { Octree } from "sparse-octree" ;
import { OctreeHelper } from "octree-helper" ;
const scene = new Scene ( ) ;
const octree = new Octree ( ) ;
const octreeHelper = new OctreeHelper ( octree ) ;
// Render the helper.
import { Vector3 } from "math-ds" ;
import { PointOctree } from "sparse-octree" ;
const min = new Vector3 ( - 1 , - 1 , - 1 ) ;
const max = new Vector3 ( 1 , 1 , 1 ) ;
const octree = new PointOctree ( min , max ) ;
const myData = { } ;
const p1 = new Vector3 ( 0 , 0 , 0 ) ;
const p2 = new Vector3 ( 0 , 0 , 0.5 ) ;
octree . insert ( p1 , myData ) ;
octree . move ( p1 , p2 ) ;
octree . get ( p2 ) ; //
				http://hi.baidu.com/onlywater/blog/item/905c5e162ed18f4021a4e9c1.html
一、八叉树基本原理：
   用八叉树来表示三维形体，并研究这种表示下的各种操作以及应用，是进入80年代后开展起来的。这种方法，既可以看成是四叉树方法在三维空间的推广，也可以认为是三维体素阵列表示形体方法的一种改进。
   八叉树的逻辑结构如下：
   假设要表...
				　　经过前面2篇WebGL射线拾取模型的文章，相信大家对射线和模型面片相交的原理已经有所了解，那么今天我们再深入探究关于射线拾取的一个问题，那就是遍历场景中的所有与射线相交的模型的优化问题。首先我们来复习一下射线拾取模型的原理，请看下图。
　　我们从上图中可以看到，在frustum视棱台区域中只有一个模型就是triangle2三角形2，那么遍历整个scene场景我们也只能取到一个geomet...
				八叉树（Octree）是一种用于表示三维空间的数据结构，常用于处理点云数据。它将三维空间划分为八个等分的立方体，每个立方体称为一个八叉树节点。八叉树是一种多层次的树结构，每个节点可以有子节点，直到达到某个终止条件。
在点云处理中，八叉树可以用来有效地表示点云数据的空间分布。通过将点云中的点逐个插入到八叉树中，可以构建出一棵完整的八叉树。在查询时，可以利用八叉树的结构进行空间上的快速搜索和遍历。
八叉树的一个重要应用是点云压缩和点云表达。通过八叉树，可以将点云数据进行分块表示，从而减少数据的存储空间和传输带宽。此外，八叉树还可以用于加速点云相关的计算任务，如点云配准、点云分割等。
总结来说，八叉树是一种用于表示三维空间的数据结构，常用于点云数据处理和压缩。它能够有效地表示点云数据的空间分布，并提供快速的查询和遍历能力。