MATLAB卷积和快速傅里叶变换
1. 卷积
卷积和解卷是信号与系统中常用的数学工具。函数conv和deconv分别为卷积和解卷函数,同时也是多项式乘法和除法(2.4.2小节)函数。
§ conv:计算向量的卷积。
语法:
conv(x,y)
如果x是输入信号,y是线性系统的脉冲过渡函数,则x和y的卷积为系统的输出信号。
§ conv2:计算二维卷积。
§ deconv:解卷积运算。
语法:
[q,r]=deconv(x,y)
解卷积和卷积的关系是:x=conv(y,q)+r。
2. 快速傅立叶变换
§ fft:一维快速傅立叶变换。
语法:
X=fft(x,N) %对离散序列进行离散傅立叶变换
说明:x可以是向量、矩阵和多维数组;N为输入变量x的序列长度,可省略,如果X的长度小于N,则会自动补零;如果X的长度大于N,则会自动截断;当N取2的整数幂时,傅立叶变换的计算速度最快。通常取大于又最靠近x长度的幂次。
一般情况下,fft求出的函数为复数,可用abs及angle分别求其幅值和相位。
§ ifft:一维快速傅立叶逆变换。
语法:
X=ifft(x,N) %对离散序列进行离散傅立叶逆变换
【例2.27】 利用傅立叶变换和卷积公式求两个离散序列的卷积。
已知:
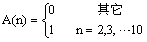
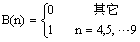
A=ones(1,10);
A(1)=0
A =
0 1 1 1 1 1 1 1 1 1
B=ones(1,9);
B([1 2 3])=0
B =
0 0 0 1 1 1 1 1 1
C=conv(A,B) %计算卷积
C =
Columns 1 through 13
0 0 0 0 1 2 3 4 5 6 6 6 6
Columns 14 through 18
5 4 3 2 1
N=32; %序列长度为32
AF=fft(A,N); %傅立叶变换
BF=fft(B,N);
CF=AF.*BF;
CC=real(ifft(CF)); %过滤掉虚部
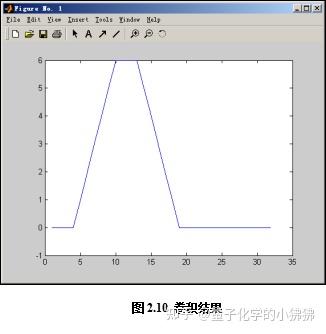
程序分析:可以看到直接计算的卷积结果C和用傅立叶变换求卷积的CC结果相同,如图2.10所示。其中序列长度N的取值应为2的整数幂,必须不小于length(A)+length(B)-1。

